字符串算法之 AC自己主动机
Posted lytwajue
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了字符串算法之 AC自己主动机相关的知识,希望对你有一定的参考价值。
近期一直在学习字符串之类的算法,感觉BF算法,尽管非常easy理解,可是easy超时,全部就想学习其它的一些字符串算法来提高一下,近期学习了一下AC自己主动机。尽管感觉有所收获,可是还是有些朦胧的感觉,在此总结一下,希望大家不吝赐教。
一、AC自己主动机的原理:
Aho-Corasick automaton。该算法在1975年产生于贝尔实验室,是著名的多模匹配算法之中的一个。
一个常见的样例就是给出N个单词,在给出一段包括m个字符的文章,让你找出有多少个单词在这文章中出现过,。要搞懂AC自己主动机。先的有字典树和KMP模式匹配算法的基础知识。
假设没有kmp或者字典树算法基础的能够看看:
<span style="font-size:18px;">//kmp http://blog.csdn.net/qq_16997551/article/details/51038525</span>
<span style="font-size:18px;">//字典树 http://blog.csdn.net/qq_16997551/article/details/51107243</span>
二、AC自己主动机算法的实现步骤(三步)
AC自己主动机的存储数据结构
const int MAXN = 10000000;
struct node
{
int count; //是否为单词最后一个节点
node *next[26];//Trie每一个节点的26个子节点
node *fail; //失败指针
};
node *q[MAXN]; //队列。採用bfs 构造失败指针
char keyword[55];//输入单词 模式串
char str[1000010];// 须要查找的 主串
int head,tail;//队列 头尾指针
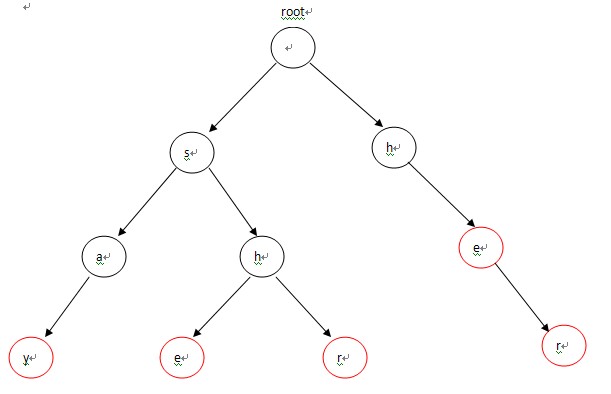
1、构造一棵Trie树
首先我们须要建立一棵Trie。
可是这棵Trie不是普通的Trie,而是带有一些特殊的性质。
首先会有3个重要的指针,分别为p, p->fail, temp。
1.指针p,指向当前匹配的字符。若p指向root,表示当前匹配的字符序列为空。
(root是Trie入口。没有实际含义)。
2.指针p->fail,p的失败指针,指向与字符p同样的结点,若没有。则指向root。
3.指针temp,測试指针(自己命名的。easy理解!~),在建立fail指针时有寻找与p字符匹配的结点的作用,在扫描时作用最大,也最不好理解。
对于Trie树中的一个节点,相应一个序列s[1...m]。此时,p指向字符s[m]。若在下一个字符处失配,即p->next[s[m+1]] == NULL,则由失配指针跳到还有一个节点(p->fail)处,该节点相应的序列为s[i...m]。若继续失配,则序列依次跳转直到序列为空或出现匹配。在此过程中。p的值一直在变化,可是p相应节点的字符没有发生变化。
在此过程中,我们观察可知,终于求得得序列s则为最长公共后缀。另外。因为这个序列是从root開始到某一节点,则说明这个序列有可能是某些序列的前缀。
再次讨论p指针转移的意义。假设p指针在某一字符s[m+1]处失配(即p->next[s[m+1]] == NULL),则说明没有单词s[1...m+1]存在。
此时。假设p的失配指针指向root,则说明当前序列的随意后缀不会是某个单词的前缀。
假设p的失配指针不指向root,则说明序列s[i...m]是某一单词的前缀,于是跳转到p的失配指针。以s[i...m]为前缀继续匹配s[m+1]。
对于已经得到的序列s[1...m],因为s[i...m]可能是某单词的后缀,s[1...j]可能是某单词的前缀,所以s[1...m]中可能会出现单词。此时,p指向已匹配的字符,不能动。
于是。令temp = p。然后依次測试s[1...m], s[i...m]是否是单词。
构造的Trie为:
实现代码:
<span style="font-size:18px;">void insert(char *word,node *root)
{
int index,len;
node *p = root,*newnode;
len = strlen(word);
for(int i=0 ;i < len ; i++ )
{
index=word[i]-'a';
if(!p->next[index])//该字符节点不存在。增加Trie树中
{
// 初始化 newnode 并 增加 Trie 树
newnode=(struct node *)malloc(sizeof(struct node));
for(int j=0;j<26;j++)
newnode->next[j]=0;
newnode->count=0;
newnode->fail=0;
p->next[index]=newnode;
}
p=p->next[index];//指针移动至下一层
}
p->count++; //单词结尾 节点 count + 1 做标记
}</span>2、构造失败指针
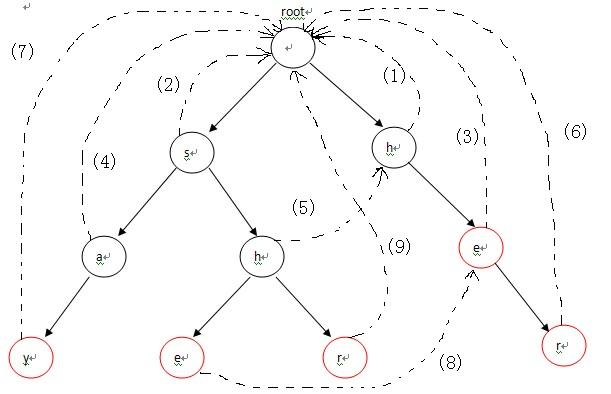
构造失败指针的过程概括起来就一句话:设这个节点上的字母为x,沿着他父亲的失败指针走,直到走到一个节点,他的儿子中也有字母为x的节点。
然后把当前节点的失败指针指向那个字符也为x的儿子。
假设一直走到了root都没找到,那就把失败指针指向root。
有两个规则:
-
root的子节点的失败指针都指向root。
-
节点(字符为x)的失败指针指向:从X节点的父节点的fail节点回溯直到找到某节点的子节点也是字符x。没有找到就指向root。
例如以下图
实现代码:
<span style="font-size:18px;">void build_ac_automation(node *root)
{
head=0;
tail=1;
q[head]=root;
node *temp,*p;
while(head<tail)//bfs构造 Trie树的失败指针
{
//算法相似 kmp ,这里相当于得到 next[]数组
//重点在于,匹配失败时,由fail指针回溯到正确的位置
temp=q[head++];
for(int i=0;i< 26 ;i ++)
{
if(temp->next[i])//推断实际存在的节点
{
// root 下的第一层 节点 的 失败指针都 指向root
if(temp==root)
temp->next[i]->fail=root;
else
{
//依次回溯 该节点的父节点的失败指针
//直到某节点的next[i]与该节点同样。则
//把该节点的失败指针指向该next[i]节点
//若回溯到 root 都没有找到,则该节点
//的失败指针 指向 root
p=temp->fail;//temp 为节点的父指针
while(p)
{
if(p->next[i])
{
temp->next[i]->fail=p->next[i];
break;
}
p=p->fail;
}
if(!p)temp->next[i]->fail=root;
}
//每处理一个点,就把它的全部儿子增加队列,
//直到队列为空
q[tail++]=temp->next[i];
}
}
}
}</span>3、模式匹配过程
从root节点開始,每次依据读入的字符沿着自己主动机向下移动。
当读入的字符。在分支中不存在时,递归走失败路径。假设走失败路径走到了root节点, 则跳过该字符。处理下一个字符。 由于AC自己主动机是沿着输入文本的最长后缀移动的,所以在读取全然部输入文本后,最后递归走失败路径,直到到达根节点, 这样能够检測出全部的模式。
搜索的步骤:
-
从根节点開始一次搜索;
-
取得要查找关键词的第一个字符。并依据该字符选择相应的子树并转到该子树继续进行检索;
-
在相应的子树上,取得要查找关键词的第二个字符,并进一步选择相应的子树进行检索。
-
迭代过程……
-
在某个节点处。关键词的全部字符已被取出,则读取附在该节点上的信息,即完毕查找。
匹配模式串中出现的单词。当我们的模式串在Trie上进行匹配时,假设与当前节点的keyword不能继续匹配的时候。
就应该去当前节点的失败指针所指向的节点继续进行匹配。
匹配过程出现两种情况:
-
当前字符匹配,表示从当前节点沿着树边有一条路径能够到达目标字符, 此时仅仅需沿该路径走向下一个节点继续匹配就可以 。目标字符串指针移向下个字符继续匹配;
-
当前字符不匹配,则去当前节点失败指针所指向的字符继续匹配,匹配过程随着指针指向root结束。
反复这2个过程中的随意一个。直到模式串走到结尾为止。
实现代码:
<span style="font-size:18px;">int query(node *root)//相似于 kmp算法。
{//i为主串指针,p为匹配串指针
int i,cnt=0,index,len=strlen(str);
node *p=root;
for(i=0; i < len ;i ++)
{
index=str[i]-'a';
//由失败指针回溯寻找,推断str[i]是否存在于Trie树中
while( !p->next[index] && p != root)
{
p=p->fail;
}
p=p->next[index];//找到后 p 指向该节点
//指针回为空。则没有找到与之匹配的字符
if(!p)
{
p=root;//指针又一次回到根节点root,下次从root開始搜索Trie树
}
node *temp=p;//匹配该节点后。沿其失败指针回溯,推断其它节点是否匹配
while(temp != root )//匹配 结束控制
{
if(temp->count>=0)//推断 该节点是否被訪问
{
//统计出现的单词个数cnt。因为节点不是单词结尾时count为0。
//故 cnt+=temp->count; 仅仅有 count >0时才真正统计了单词个数
cnt+=temp->count;
temp->count=-1; //标记已訪问
}
else
break;//节点已訪问,退出循环
temp=temp->fail;//回溯失败指针继续寻找下一个满足条件的节点
}
}
return cnt;
}</span>
三、AC自己主动机模板
<span style="font-size:18px;">#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#define kind 26
const int MAXN = 10000000;
struct node
{
int count; //是否为单词最后一个节点
node *next[26];//Trie每一个节点的26个子节点
node *fail; //失败指针
};
node *q[MAXN]; //队列,採用bfs 构造失败指针
char keyword[55];//输入单词 模式串
char str[1000010];// 须要查找的 主串
int head,tail;//队列 头尾指针
node *root;
void insert(char *word,node *root)
{
int index,len;
node *p = root,*newnode;
len = strlen(word);
for(int i=0 ;i < len ; i++ )
{
index=word[i]-'a';
if(!p->next[index])//该字符节点不存在,增加Trie树中
{
// 初始化 newnode 并 增加 Trie 树
newnode=(struct node *)malloc(sizeof(struct node));
for(int j=0;j<26;j++)
newnode->next[j]=0;
newnode->count=0;
newnode->fail=0;
p->next[index]=newnode;
}
p=p->next[index];//指针移动至下一层
}
p->count++; //单词结尾 节点 count + 1 做标记
}
void build_ac_automation(node *root)
{
head=0;
tail=1;
q[head]=root;
node *temp,*p;
while(head<tail)//bfs构造 Trie树的失败指针
{
//算法相似 kmp ,这里相当于得到 next[]数组
//重点在于,匹配失败时。由fail指针回溯到正确的位置
temp=q[head++];
for(int i=0;i< 26 ;i ++)
{
if(temp->next[i])//推断实际存在的节点
{
// root 下的第一层 节点 的 失败指针都 指向root
if(temp==root)
temp->next[i]->fail=root;
else
{
//依次回溯 该节点的父节点的失败指针
//直到某节点的next[i]与该节点同样。则
//把该节点的失败指针指向该next[i]节点
//若回溯到 root 都没有找到,则该节点
//的失败指针 指向 root
p=temp->fail;//temp 为节点的父指针
while(p)
{
if(p->next[i])
{
temp->next[i]->fail=p->next[i];
break;
}
p=p->fail;
}
if(!p)temp->next[i]->fail=root;
}
//每处理一个点,就把它的全部儿子增加队列。
//直到队列为空
q[tail++]=temp->next[i];
}
}
}
}
int query(node *root)//相似于 kmp算法。
{//i为主串指针,p为匹配串指针
int i,cnt=0,index,len=strlen(str);
node *p=root;
for(i=0; i < len ;i ++)
{
index=str[i]-'a';
//由失败指针回溯寻找,推断str[i]是否存在于Trie树中
while( !p->next[index] && p != root)
{
p=p->fail;
}
p=p->next[index];//找到后 p 指向该节点
//指针回为空。则没有找到与之匹配的字符
if(!p)
{
p=root;//指针又一次回到根节点root,下次从root開始搜索Trie树
}
node *temp=p;//匹配该节点后,沿其失败指针回溯,推断其它节点是否匹配
while(temp != root )//匹配 结束控制
{
if(temp->count>=0)//推断 该节点是否被訪问
{
//统计出现的单词个数cnt,因为节点不是单词结尾时count为0。
//故 cnt+=temp->count; 仅仅有 count >0时才真正统计了单词个数
cnt+=temp->count;
temp->count=-1; //标记已訪问
}
else
break;//节点已訪问,退出循环
temp=temp->fail;//回溯失败指针继续寻找下一个满足条件的节点
}
}
return cnt;
}
int main()
{
int i,t,n,ans;
scanf("%d",&t);
while(t--)
{
root=(struct node *)malloc(sizeof(struct node));
for(int j=0;j<26;j++) root->next[j]=0;
root->fail=0;
root->count=0;
scanf("%d",&n);
getchar();
for(i=0;i<n;i++)
{
gets(keyword);
insert(keyword,root);
}
build_ac_automation(root);
gets(str);
ans=query(root);
printf("%d\n",ans);
}
return 0;
}</span>以上是关于字符串算法之 AC自己主动机的主要内容,如果未能解决你的问题,请参考以下文章
Hnu 11187 Emoticons :-) (ac自己主动机+贪心)
POJ 1204 Word Puzzles AC自己主动机题解
HDU 3247 Resource Archiver (AC自己主动机 + BFS + 状态压缩DP)