hdu 1695 GCD（莫比乌斯入门）

Posted 2020-09-30 simpleknight

题意：求a<=x<=b ,x<=y<=d,中gcd(x,y)==k的数对个数

思路：题目可以转化成求1<=x<=b/k,1<=y<=d/k中gcd(x,y)=1的数对的个数

          我们设f(d)表示恰好gcd(x,y)==d的个数，F(d)表示gcd为d的倍数的数对个数

          F(n)=∑_d|nf(d)=> f(d)=∑_d|nu(d)F(n/d)

          令p=b/k q=d/k

          F(d)的计算十分简单 floor(p/d)*floor(q/d)

          再利用线性筛法求莫比乌斯即可

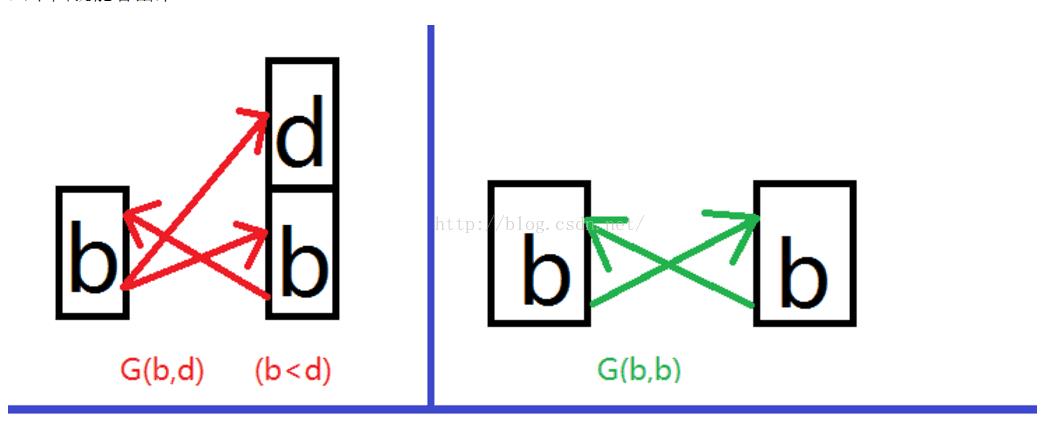
          由于题目要求（1,2）和（2,1）是一样的，所以要去掉重复的（来源见水印）

         

代码：

#include <iostream>
#include <cstring>
#define ll long long

using namespace std;

const int maxn=100005;
bool check[maxn+10];
int prime[maxn+10],mu[maxn+10],sum[maxn+10];

void Mublus()
{
    memset(check,false,sizeof(check));
    mu[1]=1;
    int tot=0;
    for(int i=2;i<=maxn;i++)
    {
        if(check[i]==false)
        {
            prime[tot++]=i;
            mu[i]=-1;
        }
        for(int j=0;j<tot;j++)
        {
            if(i*prime[j]>maxn) break;
            check[i*prime[j]]=true;
            if(i%prime[j]==0)
            {
                mu[i*prime[j]]=0;
                break;
            }
            else
            {
                mu[i*prime[j]]=-mu[i];
            }
        }
    }
}

int main()
{
    int t,cas=1;
    Mublus();
    cin>>t;
    while(t--)
    {
        int a,b,c,d,k;
        cin>>a>>b>>c>>d>>k;
        cout<<"Case "<<cas++<<": ";
        if(k==0)
        {
            cout<<"0"<<endl;
            continue;
        }
        b=b/k;
        d=d/k;
        if(b>d) swap(b,d);
        ll ans,rep;
        ans=0;
        rep=0;
        for(int i=1;i<=b;i++)
        {
            ans+=(ll)mu[i]*(b/i)*(d/i);
            rep+=(ll)mu[i]*(b/i)*(b/i);
        }
        ans=ans-rep/2;
        cout<<ans<<endl;
    }
    return 0;
}