图像的二维频谱图的理解 20170622

Posted 2020-09-30 路边的十元钱硬币

# 1 图像二维频谱长什么样子（左图是原图，右图是对应的频谱图）

 

（图片来源：第一组是来自matlab自带的图片 “cameraman.tif”；第二组是用 excel 画的，然后截图）

 

# 2 怎么获得（matlab和C++调用）

• matlaba代码，保存为 spectrum2D.m 

function [Result] = spectrum2D(I)
% I is a gray image
% \'Input Image should be gray!\' A = rgb2gray(I);

A = I; % A 要是一个灰度图像
F = fftshift(fft2(A)); % fft2() 是快速傅里叶变换函数
                       % fftshift() 目的是为了将图像横纵划分成四块，对角线互换。
                       % 经过变换以后的图像 F 中心是低频，往外频率增大。

% 以下的操作是为获得可以显示的图像。
% 如果直接显示 F ，得到的很可能是一个全白的图。
% 原因是，F内像素的值一般都很大，远大于255.
% 而matlab的imshow函数黑白对应0-255，所以不做归一化处理的图像，显示都是白色的。

B = abs(real(F)); % F 有可能是负值，而且数据是中心对称的，中心为最亮点（可以参考C++例程中的说明）
[m, n] = size(B); % 获得行数、列数
R = reshape(B, 1, m*n); % 将B映射成1行m*n列的矩阵
Temp = mapminmax(R, 0, 255); % 将R的像素值归一化到0-255之间
Result = reshape(Temp, m, n); 

% imshow(Result); % 建议调用的时候使用：imshow(spectrum2D(灰度图像矩阵))
                  % imshow(spectrum2D( rgb2gray(RGB图像矩阵)))

end

（以上三幅图，分别对应代码中的：A、F、Result）

 

抱着折腾的心态，我们把matlab的这个函数在opencv里面试着来玩一下~~不感兴趣的可以跳过。

使用opencv来调用matlab的目的在于可以方便的移植，而且方便我们可以数据进行处理；

　　比如这后面要做的峰点滤波，使得亮点更加明显。（为什么要这样做呢，那就要理解亮点的含义才可以，接着往下看。）

主要思路：1 使用matlab生成dll；2 在opencv环境中调用dll

• matlab生成dll

mex -setup
mbuild -setup
# mcc -W cpplib:名字  -T link:lib matlab文件.m
mcc -W cpplib:spectrum2D -T link:lib spectrum2D.m

• 调用opencv

// Spectrum2D.cpp : 定义控制台应用程序的入口点。
// 配置手顺：
// 1. vs2015（工程属性设置为64bit）+opencv320，64 bit windows，配置好（不懂得话去网上搜吧，很容易）。
// 2. 加载matlab生产的dll、头文件、lib，不需要cpp。（不懂得话，百度搜“怎么加载dll”）
// 3. 上步的头文件应该会提示 mclmcrrt.h mclcppclass.h找不到，这是matlab安装目录下的文件，加载到（属性->VC++ ->包含目录）
// 4. 加载matlab库文件 mclmcrrt.lib mclmcr.lib
//      （属性->VC++ ->库目录）路径：MATLAB2013a\\extern\\lib\\win64\\microsoft
// 
// 作者：路边的十元钱硬币
// 时间：20170630
// 最后的话，做注释可以的话，最好还是英文，因为vs平台，汉字注释有可能会造成编译错误。
//

#include "stdafx.h"
#include <opencv2\\opencv.hpp>
#include "spectrum2D.h"

/// mwArray 是matlab用的数据类型，不论是矩阵还是数字，当需要作为参数传递到matlab生产的函数中时，要转化成这种数据类型
/// 使用方法见代码
mwArray Mat2mwArray(cv::Mat src)
{
    CV_Assert(src.type() == CV_8UC1);

    mwArray dst(src.rows, src.cols, mxUINT8_CLASS); /// 初始化，可以理解成矩阵
    cv::Mat src_t = src.t();
    dst.SetData(src_t.data, src.rows*src.cols); /// 赋值

    return dst;
}

cv::Mat mwArry2Mat(mwArray src, int rows, int cols)
{
    if(src.IsEmpty()) /// 是否为空
        return cv::Mat();

    cv::Mat dst = cv::Mat::zeros(rows, cols, CV_64FC1);
    for(int j(0); j<rows; ++j)
    {
        double* pdata = dst.ptr<double>(j);
        for(int i(0); i<cols; ++i)
        {
            pdata[i] = src(j+1,i+1); /// 元素访问（行号，列号）
        }
    }
    
    return dst;    
}



int _tmain(int argc, _TCHAR* argv[])
{
    cv::Mat src = cv::imread("1.JPG", CV_LOAD_IMAGE_GRAYSCALE);
    cv::imshow("src", src);

    /// matlab mwArray 初始化，必须要做，不然报错
    if( !spectrum2DInitialize())
    {
        std::cout << "Could not initialize!" << std::endl;
        return -1; 
    }

    mwArray mlImg = Mat2mwArray(src);
    mwArray mlResult ;

    spectrum2D(1,mlResult, mlImg);

    /**
    简单说下mwArray的用法：
    mwArray a_int_varible(1, 1, mxINT8_CLASS); /// 定义
    mwArray a_double_varible(1, 1, mxDOUBLE_CLASS);

    a_int_varible(1,1) = 10; /// 赋值
    a_double_varible(1,1) = 10.0;

    int a = a_int_varible(1,1);

    **/

    cv::Mat result = mwArry2Mat(mlResult, src.rows, src.cols);

    cv::imshow("FFT2", result);
    cv::waitKey(0);

    return 0;
}

设置断点可以查看result矩阵中的数值。

vs需要安装插件 Image Watch

 原图是#1中的第二组图，这是其对应频谱的中心亮点的局部放大图。其中255是中心亮点，6.8616是次亮点，注意左右是对称的。

规律一：中心是最大亮点

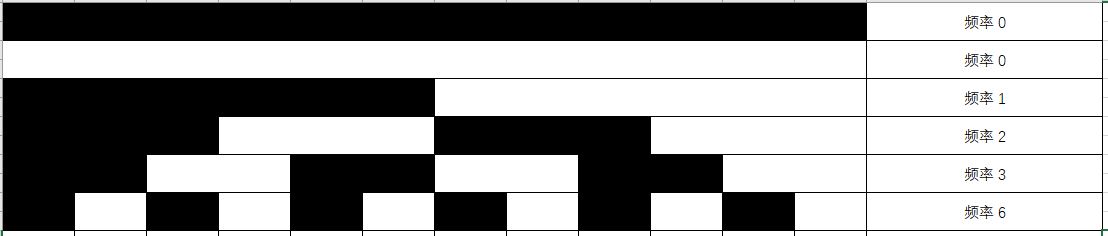
规律二：次亮点6.8616到255的距离是6，正好等于#1第二组图黑白条纹的重复次数。这不是巧合。

 

# 3 图的含义

• 先看黑白条纹的图，把图像想象成波浪，将像素点值当成起伏高度，于是获得一个水平往右（往左也无所谓）传播的“黑色波浪”。
• 在一维中，一条曲线可以被表示成很多不同频率的sin或者cos的叠加。（要问为什么的话，百度搜搜傅里叶变换相关的东西。）注意，这里的sin或者cos是二维波，只是线（y=sin(x)的图像）

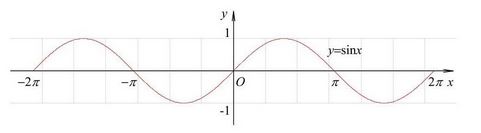
• 类似的，在图像中，每个“波浪”也可以被表示成很多不同频率的sin或者cos的叠加。注意，这里的sin或者cos函数是三维波，是曲面（y=sin(x),z=任意数）（波浪）

• 想象一幅拥有最大频率波浪的图应该是什么样的，看图。

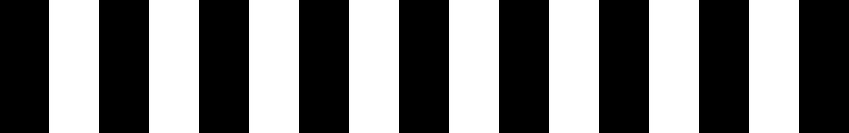
是不是应该到最后，黑或者白条纹的宽度=1个像素？对的。这就是一幅图频率的极限。

所以，得到重要结论：

• 频谱图的中心亮点，是0频率点。往外，频率增大；同一圆周上的点，频率相同。
• 频谱图的x轴的最右边点（无论是不是亮点），表示图像水平方向上的最大频率（波长是2个像素）。
• 频谱图的任意点A到中心点O的距离|OA|表示频率。

　　大家应该是有疑惑的，就是这里的关于“频率”的理解。这里说到的“频率”，可以理解成条纹出现的次数，看下图说明。

 

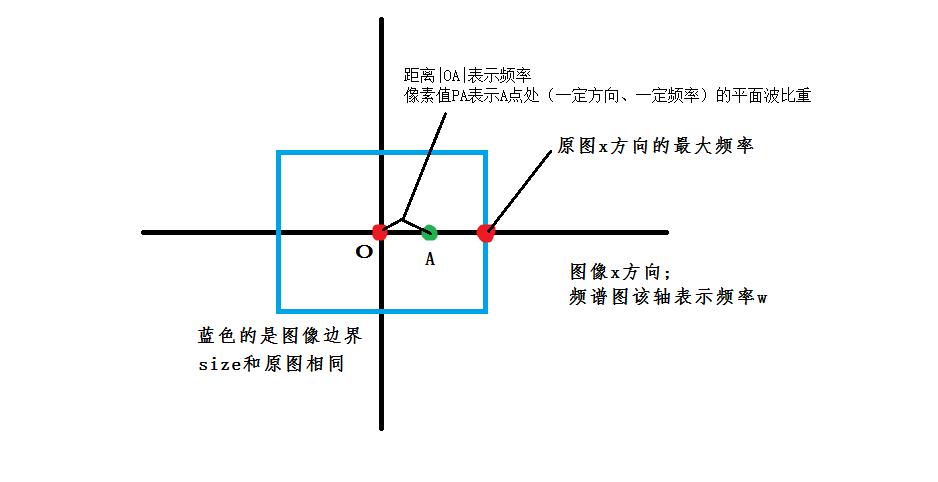
　　　　上图蓝色的为频谱图区域。其上的点A到中心点O的距离|AO|（单位像素），表示波的频率w=|OA|；其A点的像素值，表示图像中该方向（矢量OA的方向）上，频率为|AO|的比重（这里说比重而不说数量，因为频谱图的点的像素值只是响应值，只能用于对比多少。而且一般需要归一化。谈相差比例才有意义）

 

• 总结：

频谱图上任意点A，中心点O，A点像素值PA

A点的含义是：原图像上，（矢量OA）方向上的，频率为|OA|的平面波的“比重”是PA。

 

 

# 4 图的作用

|OA| = 对应A点的波浪在原图上出现的次数。

滤去某些噪声等。

 

能力有限，错误或不全之处请不吝赐教。

路边的十元钱硬币

end.