SPOJ - PGCD Primes in GCD Table（莫比乌斯反演）

Posted 2020-09-30 谦谦君子，陌上其华

http://www.spoj.com/problems/PGCD/en/

题意：

给出a，b区间，求该区间内满足gcd(x,y)=质数的个数。

 

思路：

设f（n）为 gcd（x，y）=p的个数，那么F（n）为 p | gcd（x，y）的个数，显然可得F（n）=（x/p）*（y/p）。

这道题目因为可以是不同的质数，所以需要枚举质数，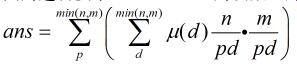

但是这样枚举太耗时，所以在这里令t=pk，

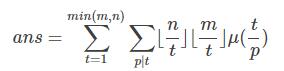
这样一来的话，我们只需要预处理u（t/p）的前缀和，之后像之前的题一样分块处理就可以了。

 1 #include<iostream>
 2 #include<algorithm>
 3 #include<cstring>
 4 #include<cstdio>
 5 #include<sstream>
 6 #include<vector>
 7 #include<stack>
 8 #include<queue>
 9 #include<cmath>
10 #include<map>
11 #include<set>
12 using namespace std;
13 typedef long long ll;
14 typedef pair<int,int> pll;
15 const int INF = 0x3f3f3f3f;
16 const int maxn = 1e7 + 100;
17 
18 int a, b;
19 
20 bool check[maxn];
21 int prime[maxn];
22 int mu[maxn];
23 ll sum[maxn];
24 
25 void Mobius()
26 {
27     memset(check, false, sizeof(check));
28     mu[1] = 1;
29     int tot = 0;
30     for (int i = 2; i <= maxn; i++)
31     {
32         if (!check[i])
33         {
34             prime[tot++] = i;
35             mu[i] = -1;
36         }
37         for (int j = 0; j < tot; j++)
38         {
39             if (i * prime[j] > maxn)
40             {
41                 break;
42             }
43             check[i * prime[j]] = true;
44             if (i % prime[j] == 0)
45             {
46                 mu[i * prime[j]] = 0;
47                 break;
48             }
49             else
50             {
51                 mu[i * prime[j]] = -mu[i];
52             }
53         }
54     }
55 
56     sum[0]=0;
57     for(int i=0;i<tot;i++)
58     {
59         for(int j=prime[i];j<maxn;j+=prime[i])
60         {
61             sum[j]+=mu[j/prime[i]];
62         }
63     }
64     for(int i=1;i<maxn;i++)
65         sum[i]+=sum[i-1];
66     return ;
67 }
68 
69 ll solve(int n, int m)
70 {
71     if(n>m)  swap(n,m);
72     ll ans=0;
73 
74     for(int i=1,last=0;i<=n;i=last+1)
75     {
76         last=min(n/(n/i),m/(m/i));
77         ans+=(sum[last]-sum[i-1])*(n/i)*(m/i);
78     }
79     return ans;
80 }
81 
82 
83 int main()
84 {
85     //freopen("in.txt","r",stdin);
86     int T;
87     Mobius();
88 
89     scanf("%d",&T);
90     while(T--)
91     {
92         scanf("%d%d",&a,&b);
93         ll ans = solve(a,b);
94         printf("%lld\\n",ans);
95     }
96     return 0;
97 }