归一化的优点和方法

Posted 2020-09-28 fisherinbox

作者：zhanlijun 

针对这个问题参考了wiki的解释： http://en.wikipedia.org/wiki/Feature_scaling。归一化后有两个好处：1）归一化后加快了梯度下降求最优解的速度；2）归一化有可能提高精度”。 

1 归一化为什么能提高梯度下降法求解最优解的速度？

斯坦福机器学习视频做了很好的解释： https://class.coursera.org/ml-003/lecture/21

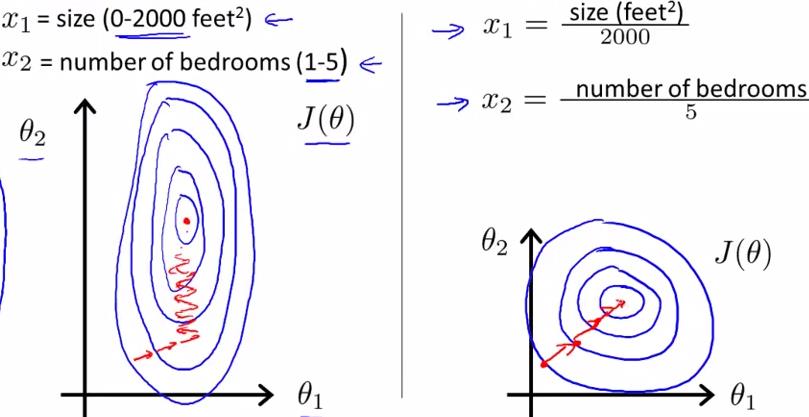
如下图所示，蓝色的圈圈图代表的是两个特征的等高线。其中左图两个特征X1和X2的区间相差非常大，X1区间是[0,2000]，X2区间是 [1,5]，其所形成的等高线非常尖。当使用梯度下降法寻求最优解时，很有可能走“之字型”路线（垂直等高线走），从而导致需要迭代很多次才能收敛； 

而右图对两个原始特征进行了归一化，其对应的等高线显得很圆，在梯度下降进行求解时能较快的收敛。 

因此如果机器学习模型使用梯度下降法求最优解时，归一化往往非常有必要，否则很难收敛甚至不能收敛。 

2 归一化有可能提高精度

一些分类器需要计算样本之间的距离（如欧氏距离），例如KNN。如果一个特征值域范围非常大，那么距离计算就主要取决于这个特征，从而与实际情况相悖（比如这时实际情况是值域范围小的特征更重要）。 

3 归一化的类型

1）线性归一化

这种归一化方法比较适用在数值比较集中的情况。这种方法有个缺陷，如果max和min不稳定，很容易使得归一化结果不稳定，使得后续使用效果也不稳定。实际使用中可以用经验常量来替代max和min。 

2）标准差标准化

经过处理的数据符合标准正态分布，即均值为0，标准差为1，其转化函数为： 

其中μ为所有样本数据的均值，σ为所有样本数据的标准差。 

3）非线性归一化

经常用在数据分化比较大的场景，有些数值很大，有些很小。通过一些数学函数，将原始值进行映射。该方法包括 log、指数，正切等。需要根据数据分布的情况，决定非线性函数的曲线，比如log(V, 2)还是log(V, 10)等。 

文章出处：http://www.cnblogs.com/LBSer/p/4440590.html