培训补坑（day3:网络流&最小割）

Posted 2020-09-28 ghostfly233

继续补坑..

第三天主要是网络流

首先我们先了解一下网络流的最基本的算法:dinic

这个算法的主要做法就是这样的：

在建好的网络流的图上从源点开始向汇点跑一遍BFS，然后如果一条边的流量不为0，那么就往下标号，

每一个点的level都是上一个点的level+1

然后在跑一遍DFS，如果发现边的两个点的level差值为1（终点比起点的level大），那么就走这条边。

那么我们首先要了解一下如何建边

网络流的最基本概念就是：可以反悔

就是说假如说我们有更好的方案，那么我们可以把原来流掉的流量再流回来。

如何做到呢？就是对于每一条边连一条方向相反，流量为0的边。

下面举图说明：

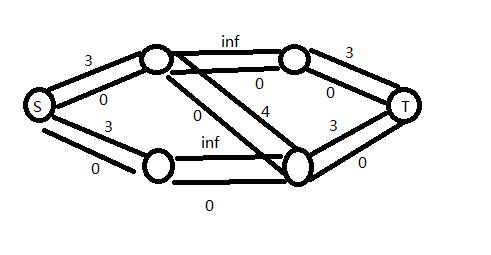
这是我们网络流的图，那么假设我们一开始走的是中间那条边，那么就是这样，我们得到的最大流是3

 

然后接下来就是我们增广的过程啦，因为我们走过的边的反向边都加上了流量，我们首先先得到一个残量网络

然后我们在又一遍bfs后我们找到这样一条路：

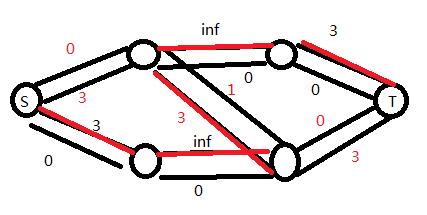
所以我们最大流+3，是不是很神奇，所以答案就是6啦；

这个过程其实就是把刚才的流量反悔，把下面的这个3的流量让给下面的一条路，自己走上面的一条路。就是。上图：

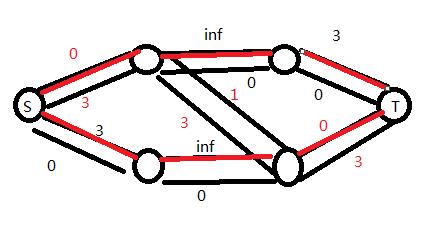
所以这样就是网络流的基本算法啦。

下面贴下代码

bool bfs(){
    int h=1,t=1;
    que[h]=S;
    level[S]=1;
    while(h<=t){
        int tmp=que[h++];
        for(int i=head[tmp];i;i=g[i].next){
            if(level[g[i].to]==-1&&g[i].w)
            level[g[i].to]=level[tmp]+1,que[++t]=g[i].to;
        }
    }
    return level[T]!=-1;
}
int dfs(int u,int v,int flow){
    if(u==v)return flow;
    int used=0;
    for(int i=head[u];i;i=g[i].next){
        if(level[g[i].to]==level[u]+1){
            int qaq=dfs(g[i].to,v,min(g[i].w,flow-used));
            if(qaq){
                g[i].w-=qaq;g[i^1].w+=qaq;used+=qaq;
                if(used==flow) return flow;
            }
        }
    }
    return used;
}
int dinic(int u,int v){
    memset(level,-1,sizeof(level));
    int tot=0;
    while(bfs()){
        tot+=dfs(S,T,inf);
        memset(level,-1,sizeof(level));
    }
    return tot;
}

————————————————我是分割线————————————————

那么我们接下来看一看最小割。

最小割的定义就是对于一个网络流的图，删掉一些边，使得从源点没有路径可以到达汇点，而花费（删掉一条边的花费就是该边的流量）的总和的最小值就是最小割。

比如下图中红色的边就是最小割

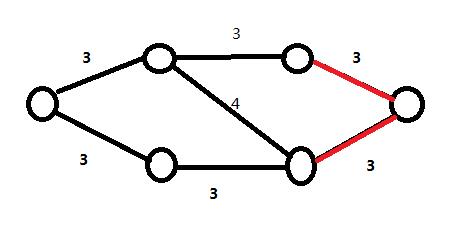
那么我们会惊奇的发现最小割就是最大流。。（至于理论我就不证明了）

——————————————我是分割线——————————————

而对于网络流这一块来说，难的不是算法本身，而是建图这一环节：

本帖着重讲解的是最小割的建图：

对于求最小割，我们一般都是要求总收益最大的一类题目，题目一般会告诉你有很多种收益，那么我们如何根据题目建图呢？

首先我们要在脑海中有一个概念，就是说我们假如说删掉一条边，意味着我们损失了一项收益，假如说我们的题目告诉我们一个项目有两种选项A,B，那么我们假设一个点割到S（表示这个点所对应的项目与T相连的边被割断，之所以这么说是因为我们有可能把一个项目拆成多个点来建图）代表的是他选择A收益，那么就说明放弃了B收益，所以B收益就是损失的一部分。

所以对于上述类型的题目，我们从S到项目连一条流量为Ai的边，从项目向汇点连一条流量为Bi的边，然后跑最大流。然后我们把所有的收益加起来-最大流（总损失）就是我们的最大收益啦！

那么还有一种题目是如果我们同时选择几种项目才能获得一项收益，对于这种图我们怎么办呢？

对于这种图，我们需要建一个辅助节点，假设我们知道多个节点都割到S才能获得这项收益，那么我们就从这些节点向辅助节点连一条流量为inf的边（表示这些边不能被割断），然后我们再从辅助节点向T连一条流量为收益大小的边，具体上图：

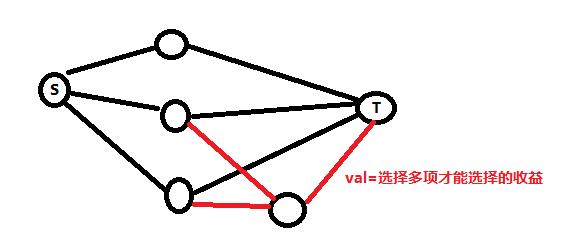
图中的两个点如果只要有一个点割到T，那么辅助节点到T的边就必须被割断（损失该项收益）

而这种辅助节点建在哪一边取决于满足条件是多个点割到S还是割到T，如果是割到S，那么辅助节点在T一侧，否则在S一侧。本类型最经典的题目就是文理分科（bzoj_3894)

下面贴上该题代码

#include<cstdio>
#include<cstring>
#define min(a,b) ((a)<(b)?(a):(b))
#define inf 0x3f3f3f3f
#define MN 30005
#define M 300005
#ifndef Debug 
    #define getchar() (SS==TT&&(TT=(SS=BB)+fread(BB,1,1<<15,stdin),TT==SS)?EOF:*SS++) 
    char BB[1<<15],*SS=BB,*TT=BB; 
#endif 
using namespace std;
inline int read(){ 
    register int x; register  bool f; register char c; 
    for (f=0; (c=getchar())<\'0\'||c>\'9\';); 
    for (x=c-\'0\'; (c=getchar())>=\'0\'&&c<=\'9\'; x=(x<<3)+(x<<1)+c-\'0\'); 
    return f?-x:x; 
} 
int n,m,sum,S,T,num=1;
int head[MN],level[MN],que[MN];
struct edge{
    int to,next,w;
}g[M];
bool bfs(){
    memset(level,-1,sizeof(level));
    int h=1,t=1;
    que[h]=S;level[S]=1;
    while(h<=t){
        int tmp=que[h++];
        for(int i=head[tmp];i;i=g[i].next)
            if(level[g[i].to]==-1&&g[i].w)
            level[g[i].to]=level[tmp]+1,que[++t]=g[i].to;
    }
    return level[T]!=-1;
}
int dfs(int u,int flow){
    if(u==T)return flow;
    int used=0;
    for(int i=head[u];i;i=g[i].next)
        if(level[g[i].to]==level[u]+1){
            int qaq=dfs(g[i].to,min(g[i].w,flow-used));
            if(qaq){
                g[i].w-=qaq;g[i^1].w+=qaq;used+=qaq;
                if(used==flow)return flow;
            }
        }
    return used;
}
int dinic(){
    int ttf=0;
    while(bfs())ttf+=dfs(S,inf);
    return ttf;
}
void ins(int u,int v,int w){g[++num].next=head[u];head[u]=num;g[num].to=v;g[num].w=w;}
void insw(int u,int v,int w){ins(u,v,w);ins(v,u,0);}
void add(int x,int u){
    if(u==S){
        insw(n+x,x,inf);
        if(x>m)insw(n+x,x-m,inf);
        if(x<=n-m)insw(n+x,x+m,inf);
        if(x%m!=0)insw(n+x,x+1,inf);
        if(x%m!=1)insw(n+x,x-1,inf);
    }
    else{
        insw(x,2*n+x,inf);
        if(x>m)insw(x-m,2*n+x,inf);
        if(x<=n-m)insw(x+m,2*n+x,inf);
        if(x%m!=0)insw(x+1,2*n+x,inf);
        if(x%m!=1)insw(x-1,2*n+x,inf);
    }
}
int main(){
    scanf("%d%d",&n,&m);S=3*n*m+1;T=S+1;n*=m;
    int x;
    for(int i=1;i<=n;i++)scanf("%d",&x),insw(S,i,x),sum+=x;
    for(int i=1;i<=n;i++)scanf("%d",&x),insw(i,T,x),sum+=x;
    for(int i=1;i<=n;i++)scanf("%d",&x),insw(S,n+i,x),add(i,S),sum+=x;
    for(int i=1;i<=n;i++)scanf("%d",&x),insw(2*n+i,T,x),add(i,T),sum+=x;
    printf("%d\\n",sum-dinic());
}

注：本题getchar快读在C++中无法运行，如要调试请删除ifndef~endif这一段，出事本人概不负责QAQ