Farm Irrigation_深搜_并查集

Posted 2020-06-25

Farm Irrigation

TimeLimit: 2000/1000 MS (Java/Others)  MemoryLimit: 65536/32768 K (Java/Others)

64-bit integer IO format:%I64d

Problem Description

Benny has a spacious farm land to irrigate. The farm land is a rectangle, and is divided into a lot of samll squares. Water pipes are placed in these squares. Different square has a different type of pipe. There are 11 types of pipes, which is marked from A to K, as Figure 1 shows. 


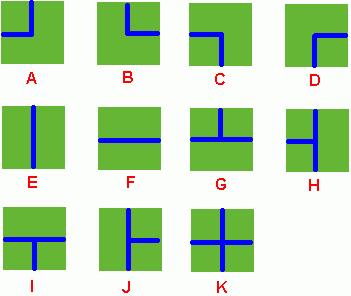
Figure 1

Benny has a map of his farm, which is an array of marks denoting the distribution of water pipes over the whole farm. For example, if he has a map 

ADC 
FJK 
IHE 

then the water pipes are distributed like 


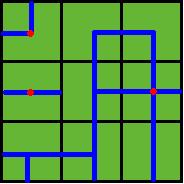
Figure 2

Several wellsprings are found in the center of some squares, so water can flow along the pipes from one square to another. If water flow crosses one square, the whole farm land in this square is irrigated and will have a good harvest in autumn. 

Now Benny wants to know at least how many wellsprings should be found to have the whole farm land irrigated. Can you help him? 

Note: In the above example, at least 3 wellsprings are needed, as those red points in Figure 2 show. 

Input

There are several test cases! In each test case, the first line contains 2 integers M and N, then M lines follow. In each of these lines, there are N characters, in the range of ‘A‘ to ‘K‘, denoting the type of water pipe over the corresponding square. A negative M or N denotes the end of input, else you can assume 1 <= M, N <= 50. 

Output

For each test case, output in one line the least number of wellsprings needed. 

SampleInput

2 2
DK
HF

3 3
ADC
FJK
IHE

-1 -1

SampleOutput

2
3

这题就是给你 不同形状 的水管， 看 哪些水管聚类连通，分成 N 堆 答案就是 N。 学长他们的第一反应是 并查集， 而我的第一反应却是 深搜。 真是囧。
这题我用了 深搜 就算了。 自己无缘无故加了好几层 映射。 搞得自己都弄糊涂了。调试了好一阵子。 真是自己找罪受。　　结果发现是 r[] 内容顺序填错。
code：

#include <cstdio>
#include <algorithm>
using namespace std;
int Map[4] = { 2, 3, 0, 1 };
int m1[3] = { 3, 0, 3 };
int m2[3] = { 3, 0, 1 };
int m3[3] = { 3, 2, 3 };
int m4[3] = { 3, 1, 2 };
int m5[3] = { 3, 0, 2 };
int m6[3] = { 3, 1, 3 };
int m7[4] = { 4, 0, 1, 3 };
int m8[4] = { 4, 0, 2, 3 };
int m9[4] = { 4, 1, 2, 3 };
int m10[4] = { 4, 0, 1, 2 };
int m11[5] = { 5, 0, 1, 2, 3 };
int r[4] = { -1, 0, 1, 0 };
int c[4] = { 0, 1, 0, -1 };
int *All[13] = { m1, m2, m3, m4, m5, m6, m7, m8, m9, m10, m11 };
const int all = 55;
char con[ all ][ all ];
int n, m, ans;
void make( int row, int column, int oper );

int main(void)
{

    char ch;
    while( scanf( "%d%d", &n, &m ) != EOF && !( n == -1 && m == -1 ) ){
        for( int i=0; i < n; ++ i ){
            getchar();
            for( int j=0; j < m; ++ j ){
                con[i][j] = getchar();
            }
        }

        ans = 0;
        for( int i=0; i < n; ++ i ){
            for( int j=0; j < m; ++ j ){
                if( con[i][j] != -1 ){
                    ++ ans;
                    ch = con[i][j] - ‘A‘;
                    make( i, j, All[ch][1] );
                }
            }
        }
        printf( "%d\n", ans );
    }
}
void make( int row, int column, int oper )
{
    char ch = con[ row ][ column ];
    int x_, y_;
    if( ch != -1 ){
        ch -= ‘A‘;
        for( int i=1; i < All[ch][0]; ++ i ){
            if( oper  ==  All[ch][i] ){
                con[row][column] = -1;
                for( int j=1; j < All[ch][0]; ++ j ){
                    x_ = row + r[ All[ch][j] ];
                    y_ = column + c[ All[ch][j] ];
                    if( x_ < 0 || x_ >= n || y_ < 0 || y_ >= m )    continue;
                    make( x_, y_, Map[ All[ch][j] ] );
                }
                break;
            }
        }
    }
}

View Code