线性表和链表

Posted 2020-09-27 翎野

原文出自：http://www.cppblog.com/cxiaojia/archive/2012/07/31/185760.html

谈到链表之前，先说一下线性表。线性表是最基本、最简单、也是最常用的一种数据结构。线性表中数据元素之间的关系是一对一的关系，即除了第一个和最后一个数据元素之外，其它数据元素都是首尾相接的。线性表有两种存储方式，一种是顺序存储结构，另一种是链式存储结构。

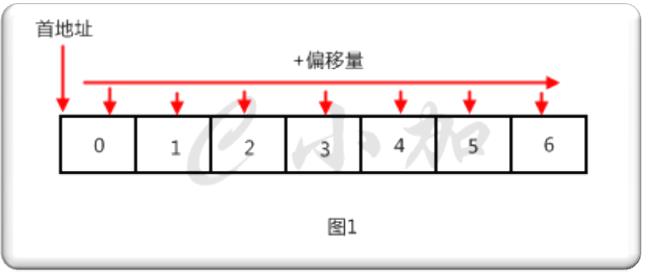
顺序存储结构就是两个相邻的元素在内存中也是相邻的。这种存储方式的优点是查询的时间复杂度为O(1)，通过首地址和偏移量就可以直接访问到某元素，关于查找的适配算法很多，最快可以达到O(logn)。缺点是插入和删除的时间复杂度最坏能达到O(n)，如果你在第一个位置插入一个元素，你需要把数组的每一个元素向后移动一位，如果你在第一个位置删除一个元素，你需要把数组的每一个元素向前移动一位。还有一个缺点，就是当你不确定元素的数量时，你开的数组必须保证能够放下元素最大数量，遗憾的是如果实际数量比最大数量少很多时，你开的数组没有用到的内存就只能浪费掉了。

我们常用的数组就是一种典型的顺序存储结构，如图1。

链式存储结构就是两个相邻的元素在内存中可能不是相邻的，每一个元素都有一个指针域，指针域一般是存储着到下一个元素的指针。这种存储方式的优点是插入和删除的时间复杂度为O(1)，不会浪费太多内存，添加元素的时候才会申请内存，删除元素会释放内存，。缺点是访问的时间复杂度最坏为O(n)，关于查找的算法很少，一般只能遍历，这样时间复杂度也是线性（O(n)）的了,频繁的申请和释放内存也会消耗时间。

顺序表的特性是随机读取，也就是访问一个元素的时间复杂度是O(1)，链式表的特性是插入和删除的时间复杂度为O(1)。要根据实际情况去选取适合自己的存储结构。

链表就是链式存储的线性表。根据指针域的不同，链表分为单向链表、双向链表、循环链表等等。

一、 单向链表（slist）

链表中最简单的一种是单向链表，每个元素包含两个域，值域和指针域，我们把这样的元素称之为节点。每个节点的指针域内有一个指针，指向下一个节点，而最后一个节点则指向一个空值。如图2就是一个单向链表。

 

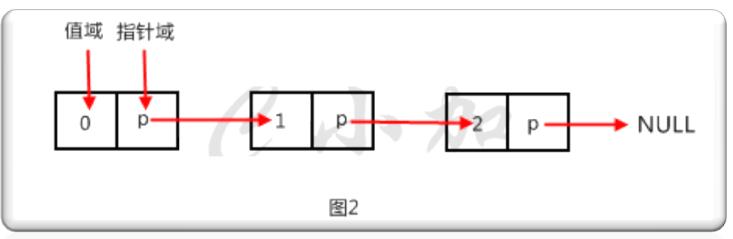
一个单向链表的节点被分成两个部分。第一个部分保存或者显示关于节点的信息，第二个部分存储下一个节点的地址。单向链表只可向一个方向遍历。

我写了一个简单的C++版单向链表类模板，就用这段代码讲解一下一个具体的单向链表该怎么写（代码仅供学习），当然首先你要具备C++基础知识和简单的模板元编程。
完整代码

首先我们要写一个节点类，链表中的每一个节点就是一个节点类的对象。如图3。

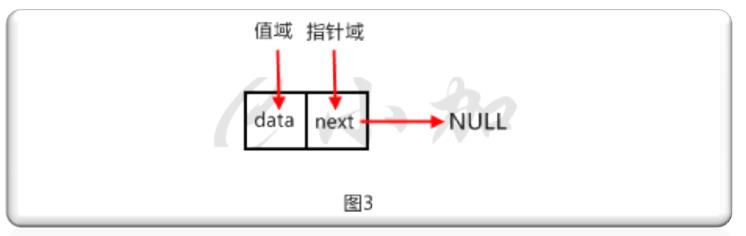
代码如下：

template<class T>
class slistNode
{
    public:
    slistNode(){next=NULL;}//初始化
    T data;//值
    slistNode* next;//指向下一个节点的指针
};

第二步，写单链表类的声明，包括属性和方法。

代码如下：

template<class T>
class myslist
{
    private:
    unsigned int listlength;
    slistNode<T>* node;//临时节点
    slistNode<T>* lastnode;//头结点
    slistNode<T>* headnode;//尾节点
    public:
        myslist();//初始化
        unsigned int length();//链表元素的个数
        void add(T x);//表尾添加元素
        void traversal();//遍历整个链表并打印
        bool isEmpty();//判断链表是否为空
        slistNode<T>* find(T x);//查找第一个值为x的节点,返回节点的地址,找不到返回NULL
        void Delete(T x);//删除第一个值为x的节点
        void insert(T x,slistNode<T>* p);//在p节点后插入值为x的节点
        void insertHead(T x);//在链表的头部插入节点
};

第三步，写构造函数，初始化链表类的属性。

代码如下：

template<class T>
myslist<T>::myslist()
{
    node=NULL;
    lastnode=NULL;
    headnode=NULL;
    listlength=0;
}

第四步，实现add()方法。

代码如下：

template<class T>
void  myslist<T>::add(T x)
{
    node=new slistNode<T>();//申请一个新的节点
    node->data=x;//新节点赋值为x
    if(lastnode==NULL)//如果没有尾节点则链表为空,node既为头结点,又是尾节点
    {
        headnode=node;
        lastnode=node;
    }
    else//如果链表非空
    {
        lastnode->next=node;//node既为尾节点的下一个节点
        lastnode=node;//node变成了尾节点,把尾节点赋值为node
    }
    ++listlength;//元素个数+1
}

第五步，实现traversal()函数，遍历并输出节点信息。

代码如下：

template<class T>
void  myslist<T>::traversal()
{
    node=headnode;//用临时节点指向头结点
    while(node!=NULL)//遍历链表并输出
    {
        cout<<node->data<<ends;
        node=node->next;
    }
    cout<<endl;
}

第六步，实现isEmpty()函数，判断链表是否为空，返回真为空，假则不空。

代码如下：

template<class T>
bool  myslist<T>::isEmpty()
{
    return listlength==0;
}

第七步，实现find()函数。

代码如下：

template<class T>
slistNode<T>* myslist<T>::find(T x)
{
    node=headnode;//用临时节点指向头结点
    while(node!=NULL&&node->data!=x)//遍历链表,遇到值相同的节点跳出
    {
        node=node->next;
    }
    return node;//返回找到的节点的地址,如果没有找到则返回NULL
}

第八步，实现delete()函数，删除第一个值为x的节点，如图4。

 

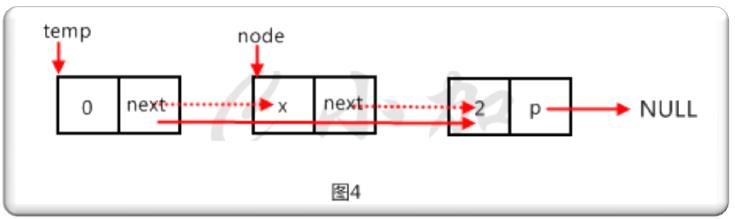
代码如下：

template<class T>
void  myslist<T>::Delete(T x)
{
    slistNode<T>* temp=headnode;//申请一个临时节点指向头节点
    if(temp==NULL) return;//如果头节点为空,则该链表无元素,直接返回
    if(temp->data==x)//如果头节点的值为要删除的值,则删除投节点
    {
        headnode=temp->next;//把头节点指向头节点的下一个节点
        if(temp->next==NULL) lastnode=NULL;//如果链表中只有一个节点,删除之后就没有节点了,把尾节点置为空
        delete(temp);//删除头节点
        return;
    }
    while(temp->next!=NULL&&temp->next->data!=x)//遍历链表找到第一个值与x相等的节点,temp表示这个节点的上一个节点
    {
        temp=temp->next;
    }
    if(temp->next==NULL) return;//如果没有找到则返回
    if(temp->next==lastnode)//如果找到的时候尾节点
    {
        lastnode=temp;//把尾节点指向他的上一个节点
        delete(temp->next);//删除尾节点
        temp->next=NULL;
    }
    else//如果不是尾节点,如图4
    {
        node=temp->next;//用临时节点node指向要删除的节点
        temp->next=node->next;//要删除的节点的上一个节点指向要删除节点的下一个节点
        delete(node);//删除节点
        node=NULL;
    }
}

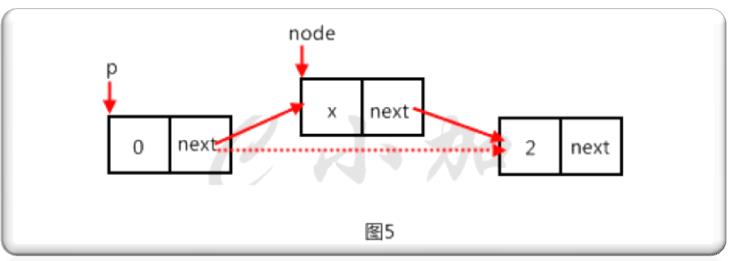
第九步，实现insert()和insertHead()函数，在p节点后插入值为x的节点。如图5。

代码如下：

template<class T>
void  myslist<T>::insert(T x,slistNode<T>* p)
{
    if(p==NULL) return;
    node=new slistNode<T>();//申请一个新的空间
    node->data=x;//如图5
    node->next=p->next;
    p->next=node;
    if(node->next==NULL)//如果node为尾节点
    lastnode=node;
}
template<class T>
void  myslist<T>::insertHead(T x)
{
    node=new slistNode<T>();
    node->data=x;
    node->next=headnode;
    headnode=node;
}

最终，我们完成一个简单的单向链表。此单向链表代码还有很多待完善的地方，以后会修改代码并不定时更新。

二、 双向链表

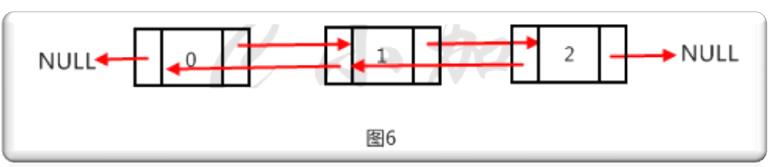
双向链表的指针域有两个指针，每个数据结点分别指向直接后继和直接前驱。单向链表只能从表头开始向后遍历，而双向链表不但可以从前向后遍历，也可以从后向前遍历。除了双向遍历的优点，双向链表的删除的时间复杂度会降为O（1），因为直接通过目的指针就可以找到前驱节点，单向链表得从表头开始遍历寻找前驱节点。缺点是每个节点多了一个指针的空间开销。如图6就是一个双向链表。

三、 循环链表

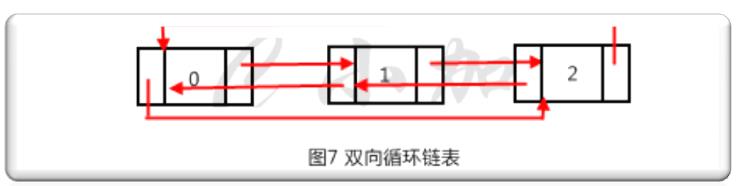
循环链表就是让链表的最后一个节点指向第一个节点，这样就形成了一个圆环，可以循环遍历。单向循环链表可以单向循环遍历，双向循环链表的头节点的指针也要指向最后一个节点，这样的可以双向循环遍历。如图7就是一个双向循环链表。