回溯3--数的拆分

Posted 2020-09-26 范仁义

回溯3--数的拆分

一、心得

 

二、题目及分析

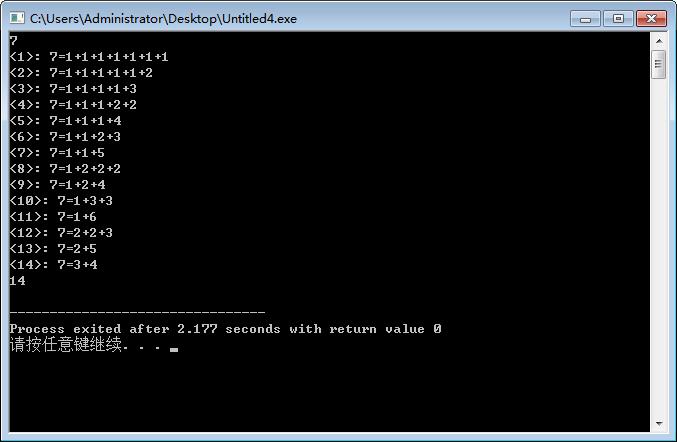
任意一个大于1的自然数n，总可以拆分成若干个小于n的自然数之和，求总的拆分方法。

这个题目里面原数据数组和标记数组都没有，只有结果数组。

 

//t是轮数也是ans的位数，print里面输出的时候t要减1,因为判断的时候是在下一轮判断的  

三、代码及结果

 1 /*
 2 任意一个大于1的自然数n，总可以拆分成若干个小于n的自然数之和，求总的拆分方法。 
 3 
 4 这个题目里面原数据数组和标记数组都没有，只有结果数组。 
 5 
 6 
 7 */ 
 8 #include <iostream>
 9 using namespace std;
10 
11 
12 int ans[10001]={1};//储存结果数组 
13 int total=0;//方案总数 
14 int n;
15 
16 void print(int t){
17     total++;
18     cout<<"<"<<total<<">"<<": ";
19     cout<<n<<"=";
20     for(int i=1;i<t;i++){
21         cout<<ans[i]<<"+";
22     } 
23     cout<<ans[t];
24     cout<<endl;
25 } 
26 
27 //t是轮数也是ans的位数，print里面输出的时候t要减1,因为判断的时候是在下一轮判断的  
28 void search(int s,int t){//t是轮数 
29     if(s==0) print(t-1);
30     for(int i=ans[t-1];i<=s;i++){
31         if(i<n){//这句话限制7=7的情况 
32             ans[t]=i;
33             search(s-i,t+1);
34             //上一步s-i，s的值没有改变，这一步不用回溯 
35         }
36     }
37 } 
38 
39 int main(){
40     cin>>n;
41     search(n,1);
42     cout<<total<<endl;
43     return 0;
44 }