BZOJ 3527: [Zjoi2014]力 FFT
Posted Meek
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了BZOJ 3527: [Zjoi2014]力 FFT相关的知识,希望对你有一定的参考价值。
3527: [Zjoi2014]力
Description
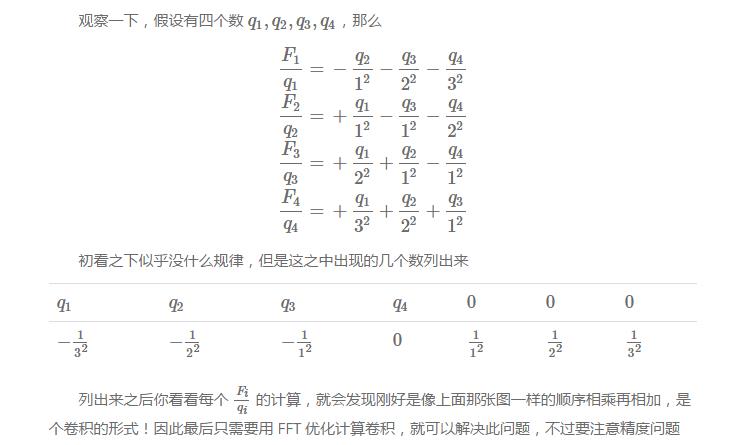
给出n个数qi,给出Fj的定义如下:

令Ei=Fi/qi,求Ei.
Input
第一行一个整数n。
接下来n行每行输入一个数,第i行表示qi。
n≤100000,0<qi<1000000000
Output
n行,第i行输出Ei。与标准答案误差不超过1e-2即可。
Sample Input
5
4006373.885184
15375036.435759
1717456.469144
8514941.004912
1410681.345880
4006373.885184
15375036.435759
1717456.469144
8514941.004912
1410681.345880
Sample Output
-16838672.693
3439.793
7509018.566
4595686.886
10903040.872
3439.793
7509018.566
4595686.886
10903040.872
HINT
Source
题解:
#include<bits/stdc++.h> using namespace std; #pragma comment(linker, "/STACK:102400000,102400000") #define ls i<<1 #define rs ls | 1 #define mid ((ll+rr)>>1) #define pii pair<int,int> #define MP make_pair typedef long long LL; const long long INF = 1e18+1LL; const double pi = acos(-1.0); const int N = 5e5+10, M = 1e3+20,inf = 2e9,mod = 1e9+7; struct Complex { double r , i ; Complex () {} Complex ( double r , double i ) : r ( r ) , i ( i ) {} Complex operator + ( const Complex& t ) const { return Complex ( r + t.r , i + t.i ) ; } Complex operator - ( const Complex& t ) const { return Complex ( r - t.r , i - t.i ) ; } Complex operator * ( const Complex& t ) const { return Complex ( r * t.r - i * t.i , r * t.i + i * t.r ) ; } } ; void FFT ( Complex y[] , int n , int rev ) { for ( int i = 1 , j , t , k ; i < n ; ++ i ) { for ( j = 0 , t = i , k = n >> 1 ; k ; k >>= 1 , t >>= 1 ) j = j << 1 | t & 1 ; if ( i < j ) swap ( y[i] , y[j] ) ; } for ( int s = 2 , ds = 1 ; s <= n ; ds = s , s <<= 1 ) { Complex wn = Complex ( cos ( rev * 2 * pi / s ) , sin ( rev * 2 * pi / s ) ) , w ( 1 , 0 ) , t ; for ( int k = 0 ; k < ds ; ++ k , w = w * wn ) { for ( int i = k ; i < n ; i += s ) { y[i + ds] = y[i] - ( t = w * y[i + ds] ) ; y[i] = y[i] + t ; } } } if ( rev == -1 ) for ( int i = 0 ; i < n ; ++ i ) y[i].r /= n ; } double q[N],num[N]; Complex s[N],t[N]; int n; int main() { scanf("%d",&n); for(int i = 1; i <= n; ++i) scanf("%lf",&q[i]); for(int i = 0; i < n-1; ++i) num[i] = (double)-1.0/(1.0*(n-i-1)*(n-i-1)); num[n-1] = 0; for(int i = n; i < 2*n-1; ++i) num[i] = (double)1.0/(1.0*(i-n+1)*(i-n+1)); int n1 = 1; for(n1=1;n1<2*n-1;n1<<=1); for(int i = 0; i < 2*n-1; ++i) s[i] = Complex(num[i],0); for(int i = 2*n-1; i < n1; ++i) s[i] = Complex(0,0); for(int i = 0; i < n; ++i)t[i] = Complex(q[i+1],0); for(int i = n; i < n1; ++i) t[i] = Complex(0,0); FFT(s,n1,1);FFT(t,n1,1); for(int i = 0; i < n1; ++i) t[i] = t[i]*s[i]; FFT(t,n1,-1); int cnt = 1; for(int i = n-1; i < 2*n-1; ++i) { printf("%.3f\\n",t[i].r); } return 0; }
以上是关于BZOJ 3527: [Zjoi2014]力 FFT的主要内容,如果未能解决你的问题,请参考以下文章