二叉查找树 Binary Serach Tree

Posted 2020-09-24

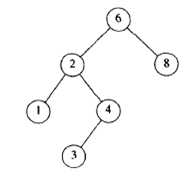
二叉查找树（Binary Serach Tree, BST）是一棵二叉树，树上每个节点存储着一个元素。对于树上每个节点X，它的左子树中所有元素均小于X，而它的右子树中所有元素均大于X。且树上不允许出现相同的节点。

这意味着只要对树做一遍中序遍历，就得到一个有序的序列。

   

屏幕剪辑的捕获时间: 2017/5/29 11:09

   

一、基本操作和实现

首先定义结点的结构。

为了避免访问NULL指针，定义一个nil节点作为哨兵节点。

constexpr int l = 0, r = 1; constexpr int inf = 0x7fffffff;

struct node; node *nil = 0, *root; struct node {     node *ch[2]; //ch[l]为左孩子, ch[r]为右孩子     int val, size, cnt; //值, 子树包含元素个数(包括重复), 结点代表元素的个数     node(int value) : val(value), size(1), cnt(1) { ch[l] = ch[r] = nil; }     void pull_up() { size = cnt + ch[l]->size + ch[r]->size; } //修正结点的size信息     int cmp(int v) { return (v < val) ? l : r; } //向左儿子走或是向右儿子走 };

void init() {     if (!nil) nil = new node(0);     nil->ch[l] = nil->ch[r] = nil;     nil->val = nil->size = nil->cnt = 0;     root = nil; }

为了方便说明，下面不区分节点和节点存储的元素。

   

查找操作

用关键字和根节点比较。当根节点存在时：

若小于根节点，则递归到左子树查找；

若大于根节点，则递归到右子树查找；

直到节点等于关键字。

若遍历到一个不存在节点的位置，则查找失败。

bool exist(int val, node *t = root) {     if (t == nil) return false;     else if (val == t->val) return true;     else return exist(val, t->ch[t->cmp(val)]); }

   

寻找最值

和查找操作类似。不过总是递归到左（或右）子树查找。当该节点不存在左（或右）儿子时，该节点就是要找的最值。

int min(node *t = root) {     if(t->ch[l] != nil) return max(t->ch[l]);     else return t->val; }

int max(node *t = root) {     if(t->ch[r] != nil) return max(t->ch[r]);     else return t->val; }

 

插入操作

和查找操作类似。

当遍历到一个不存在节点的位置时，在该节点的位置新建一个节点。

当该节点已经等于关键字时，意味着出现了重复，根据具体情况选择计数、套个另外的数据结构或者直接不处理。

注意修正size信息。

void insert(int val, node *&t = root) //传引用很重要 {     if (t == nil) t = new node(val); //找到目标位置     else if (val == t->val) t->cnt++; //重复     else insert(val, t->ch[t->cmp(val)]); //递归寻找目标     t->pull_up(); }

 

删除操作

基本上还是类似于查找操作。

找到相应结点时，先处理计数，若计数已经小于1，才需要删除。

若该节点为叶子，可以直接删除；

若只有一个儿子，可以用它的儿子代替该节点然后删除；

若有两个儿子，则用右子树中的最小节点的值代替该节点的值，这个最小节点必定没有左儿子（如果有左儿子，它的左儿子必定比它小，不符合最小节点的设定），然后通过上面两种情况删除这个最小节点。

注意修正size信息。

void remove(int val, node *&t = root) {     if (t == nil) return; //找不到目标结点     else if (val != t->val) remove(val, t->ch[t->cmp(val)]); //递归寻找结点     else if (--(t->cnt) < 1) //找到结点计数减一检查是否需要删除结点     {         if (t->ch[l] == nil || t->ch[r] == nil) //没有儿子或一个儿子         {             node *k = (t->ch[l] != nil) ? t->ch[l] : t->ch[r];             delete t;             t = k;         }         else         {             node *k = t->ch[r];             while (k->ch[l] != nil) k = k->ch[l];             t->val = k->val; t->cnt = k->cnt;             k->cnt = 1;             remove(k->val, t->ch[r]);         }     }     t->pull_up(); }

 

查找K大元素

和查找操作类似。不过是用K和左子树的秩+1比较。因为根节点就是中序遍历时的第"左子树的秩+1"个结点，也就是第"左子树的秩+1"大的结点。

若K < 左子树的秩+1，递归进入左子树查找；

若左子树的秩+1 <= K <= 左子树的秩+计数，第K大元素就是该节点；

否则递归进入右子树查找第K-(左子树的秩+计数)大结点。

注意处理K<1或k>该子树的秩的情况。

int kth(int k, node *t = root) {     if (k < 1 || k > t->size) return inf;     else if (k <= t->ch[l]->size) return kth(k, t->ch[l]); //在左子树     else if (k <= t->ch[l]->size + t->cnt) return t->val; //就是t     else return kth(k - t->ch[l]->size - t->cnt, t->ch[r]); //在右子树 }

 

统计小于X的元素个数

和查找操作类似，边查找边统计。

若该节点小于X，则给统计加上左子树的秩+计数，然后递归进入右子树；

若该节点等于X，则给统计加上左子树的秩，直接返回；

若该节点大于X，则递归进入左子树。

遍历至空节点，直接返回0。

int get_lower(int val, node *t = root) {     if (t == nil) return 0;     else if (val < t->val) return get_rank(val, t->ch[l]);     else if (val == t->val) return t->ch[l]->size;     else return t->ch[l]->size + t->cnt + get_rank(val, t->ch[r]); }

 

查询X的排名

小于X的元素个数+1

   

二、平衡二叉查找树

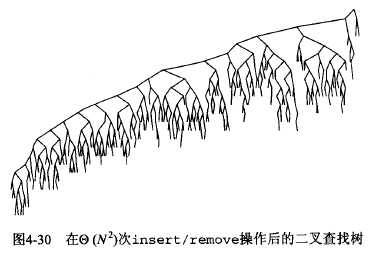
naive的BST最大的问题便是经过数次插入和删除操作后，树将会变得不平衡，甚至退化为一条链。

   

   

屏幕剪辑的捕获时间: 2017/5/29 11:34

   

为了解决这个问题，平衡二叉查找树（平衡树）应运而生。

   

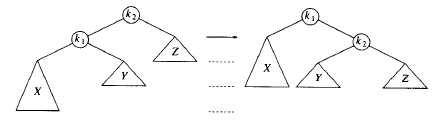
旋转操作

   

   

屏幕剪辑的捕获时间: 2017/5/29 11:48

   

旋转前，k2为父节点，k1为k2的子结点。旋转后，k1为父节点，k2为k1的子结点。旋转成功让k1上升了一层，k2下降了一层。

观察树，可以得到，旋转不破坏二叉查找树的性质。于是让k1的右儿子Y作为k2的左儿子，再让k2作为k1的右儿子，最后访问k2的父亲，让k1代替k2成为它的儿子。

几乎所有的平衡树都通过旋转操作调整树的形态使树保持平衡。

void rotate(node *&t, int d) {     node *k = t->ch[d ^ 1]; //找儿子     t->ch[d ^ 1] = k->ch[d]; //换儿子     k->ch[d] = t; //认儿子     t->pull_up(); k->pull_up();     t = k; //换父亲 }

 

常见的平衡树

现有的平衡树主要有两类：

一类要求每次插入、删除后，检查整棵树是否符合特定的平衡条件，如Treap、AVL树、红黑树、Size Balanced Tree。若不符合则通过旋转使得树重新平衡。

另一类平衡树并不强制要求树符合平衡条件，而是每次操作后都使用一次自调整操作改善平衡树，使得后面的操作效率更高。即Splay树。

   

树堆Treap

每次新建节点时给节点一个随机的优先级。从优先级的角度看时，要求树符合堆的性质，即每个节点的优先级都小于（或者都大于）两个儿子的优先级。每次插入和删除后，自底向上检查，将优先度较小的旋转到下方。

代码量小，效率高。功能简单。

   

伸展树Splay

每次访问树之后通过一系列的旋转（称为伸展）将最后一个访问的节点推上根节点的位置。

代码量较小，效率较高，支持快速合并和分裂。稍微改造可以用来维护数列（来自BST高于BST）。

   

非旋转树堆Treap

基于合并和分裂的Treap。

代码量较小，效率低，支持快速合并和分裂，同样可以用来维护数列。

   

替罪羊树Scapegoat Tree

每次插入节点后自底向上检查是否符合特定的平衡条件，以最上方的不符合条件的节点作为根，将整棵子树拆散，并重新组装成一棵平衡的二叉树。

代码量一般，平均意义下跑得飞快。

   

Size Balanced Tree

国内OI选手陈启峰发明，要求树的每个节点的一个儿子的秩（即以该节点为根节点的子树的节点数）分别大于或等于另一个儿子的两个儿子的秩。即对于节点X，满足(
。

代码量一般，效率高。

   

AVL树

要求树的每个节点的左右儿子的深度差不超过1。插入和删除后自底向上通过单旋转或双旋转调整。

代码量小，由于树趋于平衡，查找效率高，插入删除效率低。

   

红黑树

为2-3-4树的一种二叉树的实现。将2-3-4树的元素按照一定规则进行着色，按照在2-3-4树插入删除元素对应的方式维护红黑树。

代码量很大，插入效率高于AVL树，查找效率低于AVL树，综合性能最优。