素数相关？(有关素数的题持续更新中)x

Posted 云深不知处

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了素数相关？(有关素数的题持续更新中)x相关的知识，希望对你有一定的参考价值。

 素数栗子：

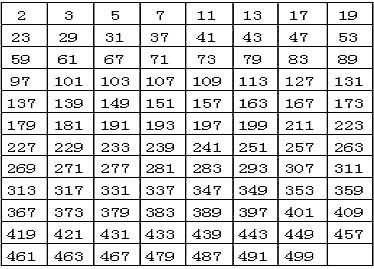
素数相关知识：

素数概念：

最大公约数只有1和它本身的数叫做质数（素数）

素数小性质：

1.大于一的整数必有素因数。

2.设p是素数，n是任意一个整数

能够推出p|n，(p,n)=1;

3.设p是素数，a，b为整数，若p|ab，则ab中至少有一个能被p整除

4.素数有无穷多个证明：

(素数与整数之间的关系：1整除2互素)

假定正整数中只有有限个素数

设p1，p2……pk为从小到大排列起来的数

且N=p1*p2*……pk

 设M=N+1

如果M为素数，那么M要大于p1，p2……pk，

所以它不在那些假设的素数集合中

若M为合数

∵任何一个合数都可以分解为几个素数的积，而N和M的最大公约数是1

∴p不可能被p1，p2……pk整除

∴该合数分解得到的素因数肯定不在假设的素数集合中。

∴无论M是素数还是合数，都意味着在假设的有限个素数之外还存在着其他素数。

∴原先的假设不成立，也就是说，素数有无穷多个。

5. 质数的个数公式 style=\'orphans: auto;text-align:start;widows: auto;-webkit-text-stroke-width: 0px; word-spacing:0px\' align=absmiddle title="" v:shapes="_x0000_i1025"> 是不减函数

6. 若n为正整数，在 align=absmiddle title="" v:shapes="_x0000_i1026"> 到  align=absmiddle title="" v:shapes="_x0000_i1027"> 之间至少有一个质数

7. 若n为大于或等于2的正整数，在n到 之间至少有一个质数

8. 若质数p为不超过n( )的最大质数，则

9. 所有大于10的质数中，个位数只有1,3,7,9

至今为止，没有任何人发现素数的分布规律，也没有人能用一个公式计算出所有的素数。

关于素数的很多的有趣的性质或者科学家的努力

1.高斯猜测，n以内的素数个数大约与n/ln(n)相当，或者说，当n很大时，两者数量级相同。这就是著名的素数定理。　　
2.十七世纪费马猜测，2的2^n次方+1，n=0，1，2…时是素数，这样的数叫费马素数，可惜当n=5时，2^32+1就不是素数，
  至今也没有找到第六个费马素数。
3.18世纪发现的最大素数是2^31-1，19世纪发现的最大素数是2^127-1，20世纪末人类已知的最大素数是2^859433-1，用十进制表示，这是一个258715位的数字。
4.孪生素数猜想：差为2的素数有无穷多对。目前知道的最大的孪生素数是1159142985×2^2304－1和1159142985×2^2304＋1。
5. 歌德巴赫猜想：大于2的所有偶数均是两个素数的和，大于5的所有奇数均是三个素数之和。其中第二个猜想是第一个的自然推论，因此歌德巴赫猜想又被称为1+ 1问题。我国数学家陈景润证明了1+2，即所有大于2的偶数都是一个素数和只有两个素数因数的合数的和。国际上称为陈氏定理。

合数概念： 

合数是除了1和它本身以外 还能被其他的正整数整除的正整数。 
除2之外的偶数都是合数。（除0以外） 
合数又名合成数，是满足以下任一（等价）条件的正整数，

　　性质 ：

　　1.是两个大于 1 的整数之乘积; 
　　2.拥有某大于 1 而小于自身的因数（因子）; 
　　3.拥有至少三个因数（因子）; 
　　4.不是 1 也不是素数(质数); 
　　5.有至少一个素因子的非素数。

筛法求素数：

若m是合数，p是m的最小正约数，所以p<=sqrt(m)；

证明：∵m为p的约数，

那么我们可以设 m=p*q；

          又∵p是最小的正约数；

          ∴q>=p;//p不等于=q且p是最小的正约数;

          ∴p*p<p*q=m;

          ∴p<=sqrt(m);

在1到m之间，运用筛法求素数：(floor为向下取整)

即在1到m中，把2到floor(sqrt(m))中素数的倍数(倍数>1)和1都去掉,其余的数就是素数；

但是有一点要注意的是：

运用筛法，只能求1到m之间的素数，但是不能求n到m之间的素数

基本判断思路：

①在一般领域，对正整数n，如果用2到sqrt(n)之间的所有整数去除，均无法整除，则n为质数。

②质数大于等于2

③不能被它本身和1以外的数整除

给出代码：

我自己胡乱搞的方法：

int pd(int x)
{
    if(x==2||x==3) return 1;
    if(x%2==0 || x==1) return 0;
    int j=3;
    while(j<=sqrt(x)&&x%j!=0) j+=2;
    if(x%j==0) return 0;
    else return 1;
}

普通方法直接来判断是否为素数：

#include <iostream>
#include <cmath>
using namespace std;

int main() {
    int b;
    while(cin>>b) {
        if(b<0) {
            cout<<"It\'s can\'t a prime! Because it\'s tan 90 ^_^, Don\'t ask me why!"<<endl;
            continue;
        }
        if(b<=1 && b>=0) {
            cout<<"It\'s not a prime! Because it\'s rules!"<<endl;
            continue;
        }
        bool ok=true;
        for(int i=2; i<=sqrt(b); ++i) {
            if(b%i==0) {
                ok=false;
                cout<<"It\'s not a prime, because of the smallest number "<<i<<endl;
                break;
            }
        }
        if(ok)
            cout<<"Yes, this is a prime!"<<endl;
    }
    return 0;
}

经典的Eraosthenes筛法：

#include <iostream>
#include <cmath>
using namespace std;

const int Maxn = 10000001;
int n,cnt; 
int prime[Maxn];
bool notprime[Maxn];

void Eraosthenes_pre() {
    for(int i=2; i<sqrt(n); ++i) {
        if(notprime[i])
            continue;
        for(int j=i; i*j<n; ++j)
            notprime[i*j]=true;
    }
    for(int i=2; i<n; ++i)
        if(!notprime[i])
            prime[cnt++]=i;
}

int main() {
    cin>>n;
    Eraosthenes_pre();
    for(int i=0; i<cnt; ++i) 
        cout<<prime[i]<<endl;
    return 0;
}

但是Eraosthenes筛法的速度并不快，原因在于对于一个合数，这种方法会重复的标记。

一种线性筛素数的方法有效的解决了这一点。

线性筛代码如下：

void get_prime() {
    notprime[0]=notprime[1]=true;
    for(int i=2; i<=n; ++i) {
        if(!notprime[i])
            prime[++cnt]=i;
        for(int j=1; j<=cnt && i*prime[j]<=n; ++j) {
            notprime[i*prime[j]]=true;
            if(i%prime[j]==0)
                break;
        }
    }
}

小知识点：

唯一分解定理定义：

任意大于1的整数，若不计因子排列顺序，都可以被唯一分解为素数(不会是只有2个素数的乘积，可能是多个)的乘积；

n=p1α1×p2α2×……×psαs

pi(i=1,2,……，s)为两两互不相等的素数，

αi(i=1,2,……，s)为正整数；

举个栗子：56=2^3*7；

C++代码实现：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#define maxn 10086

using namespace std;

bool ss[maxn];
int css[maxn],num;
int ans[maxn],times[maxn],cnt;
int n;

void zss()
{
    memset(ss,1,sizeof(ss));
    ss[1]=0;
    for(int i=2;i<=maxn;i++)
        if(ss[i])
        {
            css[++num]=i;
            for(int j=2;j*i<=maxn;j++)ss[i*j]=0;
        }
}
int main()
{
    scanf("%d",&n);
    printf("%d=",n);
    zss();
    int k=1;
    while(n!=1&&k<=num)
    {
        int p=0;
        if(n%css[k]==0)
        {
            while(n%css[k]==0)
            {
                n/=css[k];
                p++;
            }
            ans[++cnt]=css[k];
            times[cnt]=p;
        }
        k++;
    }
    for(int i=1;i<cnt;i++)
        if(times[i]!=1) printf("%d^%d*",ans[i],times[i]);
        else printf("%d*",ans[i]);
    if(times[cnt]==1) printf("%d",ans[cnt]);
    else printf("%d^%d",ans[cnt],times[cnt]);
    return 0;
}
View Code

例题 

例题1：质因数分解

总时间限制:
　　1000ms
内存限制: 
　　65536kB
描述

已知正整数 n 是两个不同的质数的乘积，试求出较大的那个质数。

输入
输入只有一行，包含一个正整数 n。

对于60%的数据，6 ≤ n ≤ 1000。
对于100%的数据，6 ≤ n ≤ 2*10^9。
输出
输出只有一行，包含一个正整数 p，即较大的那个质数。
样例输入
21
样例输出
　　　　7
思路:

　　根据唯一分解定理，若此题有答案，则输入数据满足有且只有一组质数相乘=n

　　所以，i从2循环到根号n，如果n%i==0，则n/i为答案

　　也就是说，n=质数a*质数b，n没有其他的分解

证明：

　　假设还有另外一组分解c*d

　　那么c*d分解质因数的结果与a*b相同

　　又因为a、b是质数

　　所以a*b分解质因数=a*b

　　所以c=a，d=b

　　即只有一种分解

 c++代码实现：

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;

int pd(int x) {
    if(x==2 || x==3) return 1;
    if(x%2==0 || x==1) return 0;
    int j=3;
    while(j<=sqrt(x) && x%j!=0) j+=2;
    if(x%j==0) return 0;
    else return 1;
}

int main() {
    int n;
    scanf("%d",&n);
    int t=sqrt(n); //i最大的范围
    for(int i=2; i<=t; i++) { //因为1不是质数，所以循环从2开始进行
        if(n%i==0) { //如果找到了能够进行整除的i
            //又因为样例说一定满足n 是两个不同的质数的乘积，所以直接输出另外一个数就行
            //if(pd(i)) {//所以由上得：不需要判断第一个数是否能够被模 ,即满足唯一分解定理
                printf("%d",n/i);
                return 0;
//            }
        }
    }
    return 0;
}
View Code

例题2：第n小质数

总时间限制:
 　　1000ms
内存限制: 
　　65536kB
描述

输入一个正整数n，求第n小的质数。

输入
一个不超过10000的正整数n。
输出
第n小的质数。
样例输入
10
样例输出
　　　　29
坑点:
一定要注意范围!!!!范围!!!!范围!!!!
c++代码实现
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
/*
#define M 10001这里！！数组开的不能太小!!!
上面跟下面选取一个进行改正
*/
#define M 10002
using namespace std;

struct Q {
    int top;
    Q() { top=0; }
    int s[M];
    void jiajia() { top++; }
    int add(int x) { s[top]=x; }
} q;

int pd(int x) {
    if(x==2 || x==3) return 1;
    if(x%2==0 || x==1) return 0;
    int j=3;
    while(j<=sqrt(x) && x%j!=0) j+=2;
    if(x%j==0) return 0;
    else return 1;
}

void Q_work() {
    q.jiajia();
    q.add(2);
    for(int i=3;; i++) {
        if(pd(i)) {
            q.jiajia();
            q.add(i);
        }
        if(q.top>10000) //因为结束条件是q.top>10000所以需要使用到10001个,所以数组需要开到10002
            //if(q.top>=10000) 或者上面不改,改这里
            break;
    }
}

int main() {
    int n;
    scanf("%d",&n);
    Q_work();
    printf("%d",q.s[n]);
    return 0;
}
View Code

例题3：1530 大质数 

题目描述 Description

小明因为没做作业而被数学老师罚站，之后数学老师要他回家把第n个质数找出来。（1<=n<=100000)

老师随机写了几个数，交给了小明。小明百度找了很久，都没能解决。现在交给聪明的你。请你帮忙！

—————————————————————————————————————————————

简单描述：把第n个质数找出来。

输入描述 Input Description

一个正整数n。

（1<=n<=100000)

输出描述 Output Description

第n个质数。

（第1个质数为2，第2个质数为3。）

样例输入 Sample Input

样例1

2

样例2

65

样例3

20133

样例输出 Sample Output

样例1

3

样例2

313

样例3

226381

c++代码实现

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;

int pd(int x) {
    if(x==2 || x==3) return 1;
    if(x%2==0 || x==1) return 0;
    int j=3;
    while(j<=sqrt(x)&&x%j!=0) j+=2;
    if(x%j==0) return 0;
    else return 1;
}

int n,ans,js;
void Q_work() {
    if(n==1) {
        cout<<"2";
        return;
    }
    js=1;
    for(int i=2; js!=n; i++) {
        if(pd(i)) {
            ans=i;
            js++;
        }
    }
    printf("%d",ans);
}

int main() {
    scanf("%d",&n);
    Q_work();
    return 0;
}
View Code 1
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#define M 100001
using namespace std;

struct Q {
    int top;
    Q() {
        top=0;
    }
    int s[M];
    void jiajia() {
        top++;
    }
    int add(int x) {
        s[top]=x;
    }
} q;

int pd(int x) {
    if(x==2 || x==3) return 1;
    if(x%2==0 || x==1) return 0;
    int j=3;
    while(j<=sqrt(x)&&x%j!=0) j+=2;
    if(x%j==0) return 0;
    else return 1;
}

int n;
void Q_work() {
    q.jiajia();
    q.add(2);
    for(int i=3;; i++) {
        if(pd(i)) {
            q.jiajia();
            q.add(i);
        }
        if(q.top>=n)
            break;
    }
}

int main() {
    scanf("%d",&n);
    Q_work();
    printf("%d",q.s[n]);
    return 0;
}
View Code 2

例题4：判决素数个数

总时间限制: 
1000ms
内存限制: 
65536kB
描述

输入两个整数X和Y，输出两者之间的素数个数（包括X和Y）。

输入
两个整数X和Y（1 <= X,Y <= 105）。
输出
输出一个整数，表示X，Y之间的素数个数（包括X和Y）。
样例输入
　　1 100
样例输出
　　25
思路:
　　这道题有个大坑!!!!给的数据有可能x>y!!!!
c++代码实现
#include<iostream>
#include<cstdio> 
using namespace std;

int main() {
    int x,y,n,t;
    cin>>x>>y;
    if(x>y) {//进行交换，使得小数在前
        t=x;x=y;y=t;
    }
    浅谈线性素数筛


 数论基础学习总结（持续补充中）


 欧拉函数（模板，相关问题持续更新中）


 求C语言中 判断素数的 代码!!!!!


 素数相关知识


 判断素数