常见算法

Posted 2020-09-21 小花猫

 

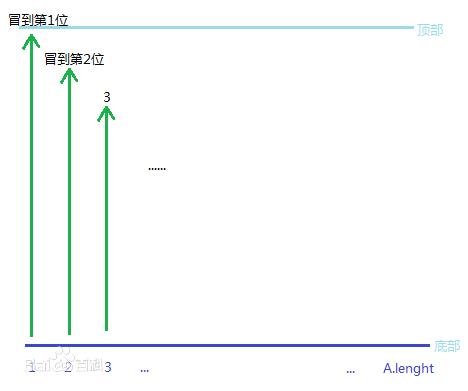
1 冒泡排序（Bubble Sort）

 

冒泡排序（Bubble Sort），是一种计算机科学领域的较简单的排序算法。

它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。

这个算法的名字由来是因为越大的元素会经由交换慢慢“浮”到数列的顶端，故名。

 1 # -*- coding:utf-8 -*-
 2 __author__ = \'liulin\'
 3 
 4 data_set = [ 9,1,22,31,45,3,6,2,11 ]
 5 
 6 loop_count = 0
 7 data_len = len(data_set)
 8 for i in range(len(data_set) -1):
 9     for j in range(len(data_set) - j- 1):
13         if data_set[j] > data_set[j+1]: 
14             data_set[j+1],data_set[j] = data_set[j],data_set[j+1]
15         loop_count +=1
16     print(data_set)
17 print(data_set)
18 print("loop times", loop_count)

 总结: 相邻的元素进行比较,大的往后走,就是前后交换,元素的间隔就是一次比较的次数,加深对for循环的理解,第一个for循环决定了大的循环走几轮,第二个for循环表示这个是否要交换,两层for循环分工合作,理解for循环的跳出　

 

2 插入排序(Insertion Sort)

 

有一个已经有序的数据序列，要求在这个已经排好的数据序列中插入一个数，但要求插入后此数据序列仍然有序，这个时候就要用到一种新的排序方法——插入排序法,插入排序的基本操作就是将一个数据插入到已经排好序的有序数据中，从而得到一个新的、个数加一的有序数据，算法适用于少量数据的排序，时间复杂度为O(n^2)。是稳定的排序方法。插入算法把要排序的数组分成两部分：第一部分包含了这个数组的所有元素，但将最后一个元素除外（让数组多一个空间才有插入的位置），而第二部分就只包含这一个元素（即待插入元素）。在第一部分排序完成后，再将这个最后元素插入到已排好序的第一部分中。

插入排序的基本思想是：每步将一个待排序的纪录，按其关键码值的大小插入前面已经排序的文件中适当位置上，直到全部插入完为止。

 

 

1 2 3 4 5 6 7 8 9 10 11 12 13

source = [92, 77, 67, 8, 6, 84, 55, 85, 43, 67]       for index in range(1,len(source)):     current_val = source[index] #先记下来每次大循环走到的第几个元素的值     position = index        while position > 0 and source[position-1] > current_val: #当前元素的左边的紧靠的元素比它大,要把左边的元素一个一个的往右移一位,给当前这个值插入到左边挪一个位置出来         source[position] = source[position-1] #把左边的一个元素往右移一位         position -= 1 #只一次左移只能把当前元素一个位置 ,还得继续左移只到此元素放到排序好的列表的适当位置 为止        source[position] = current_val #已经找到了左边排序好的列表里不小于current_val的元素的位置,把current_val放在这里     print(source)

结果：

[77, 92, 67, 8, 6, 84, 55, 85, 43, 67]
[67, 77, 92, 8, 6, 84, 55, 85, 43, 67]
[8, 67, 77, 92, 6, 84, 55, 85, 43, 67]
[6, 8, 67, 77, 92, 84, 55, 85, 43, 67]
[6, 8, 67, 77, 84, 92, 55, 85, 43, 67]
[6, 8, 55, 67, 77, 84, 92, 85, 43, 67]
[6, 8, 55, 67, 77, 84, 85, 92, 43, 67]
[6, 8, 43, 55, 67, 77, 84, 85, 92, 67]
[6, 8, 43, 55, 67, 67, 77, 84, 85, 92]

 

 

 

二分查找

 

　折半查找法也称为二分查找法，它充分利用了元素间的次序关系，采用分治策略，可在最坏的情况下用O(log n)完成搜索任务。它的基本思想是，将n个元素分成个数大致相同的两半，取a[n/2]与欲查找的x作比较，如果x=a[n/2]则找到x，算法终止。如 果x<a[n/2]，则我们只要在数组a的左半部继续搜索x（这里假设数组元素呈升序排列）。如果x>a[n/2]，则我们只要在数组a的右 半部继续搜索x

 1 def bin_search(data_list, val):    
 2     low = 0                         # 最小数下标    
 3     high = len(data_list) - 1       # 最大数下标    
 4     while low <= high:        
 5         mid = (low + high) // 2     # 中间数下标        
 6         if data_list[mid] == val:   # 如果中间数下标等于val, 返回            
 7             return mid        
 8         elif data_list[mid] > val:  # 如果val在中间数左边, 移动high下标            
 9             high = mid - 1        
10         else:                       # 如果val在中间数右边, 移动low下标            
11             low = mid + 1    
12      return # val不存在, 返回None
13 ret = bin_search(list(range(1, 10)), 3)
14 print(ret)

 

　

快速排序（quick sort）

 

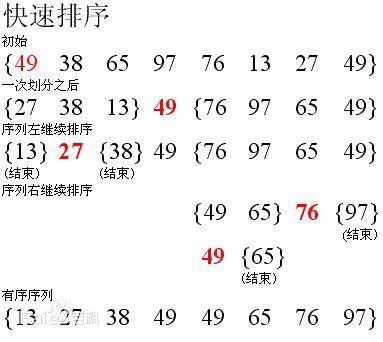
快速排序由C. A. R. Hoare在1962年提出。它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

def quick_sort(lists, left, right):

    # 快速排序

    if left >= right:

        return lists

    key = lists[left]

    low = left

    high = right

    while left < right:

        while left < right and lists[right] >= key:

            right -= 1

        lists[left] = lists[right]

        while left < right and lists[left] <= key:

            left += 1

        lists[right] = lists[left]

    lists[right] = key

    quick_sort(lists, low, left - 1)

    quick_sort(lists, left + 1, high)

    return lists

 

　

 1 void sort(int *a, int left, int right)
 2 {
 3     if(left >= right)/*如果左边索引大于或者等于右边的索引就代表已经整理完成一个组了*/
 4     {
 5         return ;
 6     }
 7     int i = left;
 8     int j = right;
 9     int key = a[left];
10       
11     while(i < j)                               /*控制在当组内寻找一遍*/
12     {
13         while(i < j && key <= a[j])
14         /*而寻找结束的条件就是，1，找到一个小于或者大于key的数（大于或小于取决于你想升
15         序还是降序）2，没有符合条件1的，并且i与j的大小没有反转*/ 
16         {
17             j--;/*向前寻找*/
18         }
19           
20         a[i] = a[j];
21         /*找到一个这样的数后就把它赋给前面的被拿走的i的值（如果第一次循环且key是
22         a[left]，那么就是给key）*/
23           
24         while(i < j && key >= a[i])
25         /*这是i在当组内向前寻找，同上，不过注意与key的大小关系停止循环和上面相反，
26         因为排序思想是把数往两边扔，所以左右两边的数大小与key的关系相反*/
27         {
28             i++;
29         }
30           
31         a[j] = a[i];
32     }
33       
34     a[i] = key;/*当在当组内找完一遍以后就把中间数key回归*/
35     sort(a, left, i - 1);/*最后用同样的方式对分出来的左边的小组进行同上的做法*/
36     sort(a, i + 1, right);/*用同样的方式对分出来的右边的小组进行同上的做法*/
37                        /*当然最后可能会出现很多分左右，直到每一组的i = j 为止*/
38 }

 

希尔排序（shell sort）

希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本,该方法的基本思想是：先将整个待排元素序列分割成若干个子序列（由相隔某个“增量”的元素组成的）分别进行直接插入排序，然后依次缩减增量再进行排序，待整个序列中的元素基本有序（增量足够小）时，再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下（接近最好情况），效率是很高的，因此希尔排序在时间效率比直接插入排序有较大提高

首先要明确一下增量的取法：

      第一次增量的取法为： d=count/2;

      第二次增量的取法为:  d=(count/2)/2;

      最后一直到: d=1;

看上图观测的现象为：

        d=3时：将40跟50比，因50大，不交换。

                   将20跟30比，因30大，不交换。

                   将80跟60比，因60小，交换。

        d=2时：将40跟60比，不交换，拿60跟30比交换，此时交换后的30又比前面的40小，又要将40和30交换，如上图。

                   将20跟50比，不交换，继续将50跟80比，不交换。

        d=1时：这时就是前面讲的插入排序了，不过此时的序列已经差不多有序了，所以给插入排序带来了很大的性能提高。

 

import time,random

#source = [8, 6, 4, 9, 7, 3, 2, -4, 0, -100, 99]
#source = [92, 77, 8,67, 6, 84, 55, 85, 43, 67]

source = [ random.randrange(10000+i) for i in range(10000)]
#print(source)



step = int(len(source)/2) #分组步长

t_start = time.time()


while step >0:
    print("---step ---", step)
    #对分组数据进行插入排序

    for index in range(0,len(source)):
        if index + step < len(source):
            current_val = source[index] #先记下来每次大循环走到的第几个元素的值
            if current_val > source[index+step]: #switch
                source[index], source[index+step] = source[index+step], source[index]

    step = int(step/2)
else: #把基本排序好的数据再进行一次插入排序就好了
    for index in range(1, len(source)):
        current_val = source[index]  # 先记下来每次大循环走到的第几个元素的值
        position = index

        while position > 0 and source[
                    position - 1] > current_val:  # 当前元素的左边的紧靠的元素比它大,要把左边的元素一个一个的往右移一位,给当前这个值插入到左边挪一个位置出来
            source[position] = source[position - 1]  # 把左边的一个元素往右移一位
            position -= 1  # 只一次左移只能把当前元素一个位置 ,还得继续左移只到此元素放到排序好的列表的适当位置 为止

        source[position] = current_val  # 已经找到了左边排序好的列表里不小于current_val的元素的位置,把current_val放在这里
    print(source)

t_end = time.time() - t_start

print("cost:",t_end)