MATLAB常微分方程的数值解法

Posted 2020-09-21 凯鲁嘎吉

MATLAB常微分方程的数值解法

作者：凯鲁嘎吉 - 博客园
http://www.cnblogs.com/kailugaji/

一、实验目的

科学技术中常常要求解常微分方程的定解问题，所谓数值解法就是求未知函数在一系列离散点处的近似值。

二、实验原理

三、实验程序

  1. 尤拉公式程序

四、实验内容

选一可求解的常微分方程的定解问题，分别用以上1, 4两种方法求出未知函数在

节点处的近似值，并对所求结果与分析解的（数值或图形）结果进行比较。

 

五、解答

1. 程序

求解初值问题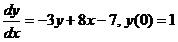

取n=10

源程序：

euler23.m:

function [A1,A2,B1,B2,C1,C2]=euler23(a,b,n,y0)
%欧拉法解一阶常微分方程
%初始条件y0
h = (b-a)/n; %步长h
%区域的左边界a
%区域的右边界b
x = a:h:b; 
m=length(x);
 
%前向欧拉法
y = y0;
for i=2:m
    y(i)=y(i-1)+h*oula(x(i-1),y(i-1));  
    A1(i)=x(i);
    A2(i)=y(i);
end
plot(x,y,\'r-\');
hold on;
 
%改进欧拉法
y = y0;
for i=2:m
    y(i)=y(i-1)+h/2*( oula(x(i-1),y(i-1))+oula(x(i),y(i-1))+h*(oula(x(i-1),x(i-1)))); 
    B1(i)=x(i);
    B2(i)=y(i);
end
plot(x,y,\'m-\');
hold on;
 
%欧拉两步公式
y=y0;
y(2)=y(1)+h*oula(x(1),y(1));  
for i=2:m-1
    y(i+1)=y(i-1)+2*h*oula(x(i),y(i));
    C1(i)=x(i);
    C2(i)=y(i);
end
plot(x,y,\'b-\');
hold on;
 
%精确解用作图
xx = x;
f = dsolve(\'Dy=-3*y+8*x-7\',\'y(0)=1\',\'x\');%求出解析解
y = subs(f,xx); %将xx代入解析解，得到解析解对应的数值
 
plot(xx,y,\'k--\');
legend(\'前向欧拉法\',\'改进欧拉法\',\'欧拉两步法\',\'解析解\');

oula.m:
function f=oula(x,y)
f=-3*y+8*x-7;

　　

2. 运算结果

    A1,A2为前向欧拉法在节点处的近似值，B1,B2为改进的欧拉法在节点处的近似值，C1,C2为欧拉公式法在节点处的近似值。

>> [A1,A2,B1,B2,C1,C2]=euler23(0,1,10,1)

A1 =

         0    0.1000    0.2000    0.3000    0.4000    0.5000    0.6000    0.7000    0.8000    0.9000    1.0000


A2 =

         0         0   -0.6200   -0.9740   -1.1418   -1.1793   -1.1255   -1.0078   -0.8455   -0.6518   -0.4363


B1 =

         0    0.1000    0.2000    0.3000    0.4000    0.5000    0.6000    0.7000    0.8000    0.9000    1.0000


B2 =

         0    0.0050   -0.6090   -0.9563   -1.1169   -1.1468   -1.0853   -0.9597   -0.7893   -0.5875   -0.3638


C1 =

         0    0.1000    0.2000    0.3000    0.4000    0.5000    0.6000    0.7000    0.8000    0.9000


C2 =

         0         0   -0.2400   -0.9360   -0.5984   -1.3370   -0.3962   -1.5392    0.2473   -1.8076

>> [A1,A2,B1,B2,C1,C2]=euler23(0,1,10,1)

A1 =

         0    0.1000    0.2000    0.3000    0.4000    0.5000    0.6000    0.7000    0.8000    0.9000    1.0000


A2 =

         0         0   -0.6200   -0.9740   -1.1418   -1.1793   -1.1255   -1.0078   -0.8455   -0.6518   -0.4363


B1 =

         0    0.1000    0.2000    0.3000    0.4000    0.5000    0.6000    0.7000    0.8000    0.9000    1.0000


B2 =

         0    0.0050   -0.6090   -0.9563   -1.1169   -1.1468   -1.0853   -0.9597   -0.7893   -0.5875   -0.3638


C1 =

         0    0.1000    0.2000    0.3000    0.4000    0.5000    0.6000    0.7000    0.8000    0.9000


C2 =

         0         0   -0.2400   -0.9360   -0.5984   -1.3370   -0.3962   -1.5392    0.2473   -1.8076

　　

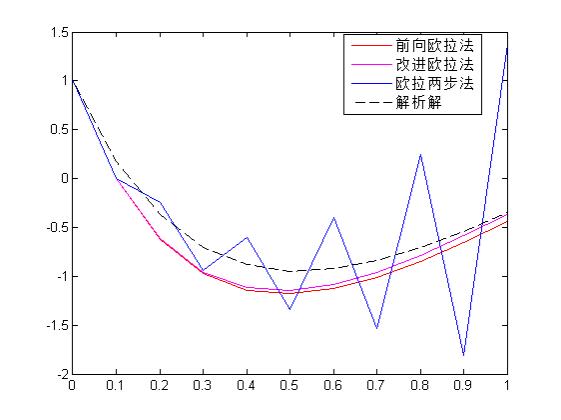
3. 拓展（方法改进、体会等）

从以上图形可以看出，在n=10时，改进的欧拉法精度更高，而欧拉两步法所求结果震荡不收敛，越接近1，震荡幅度越大，于是取n=100,时，结果如下所示：

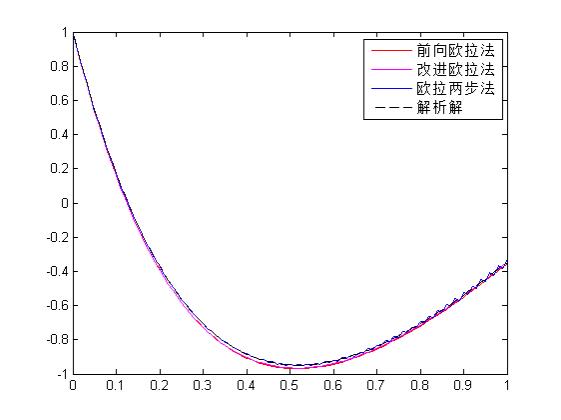
当n=1000时，结果如下图：

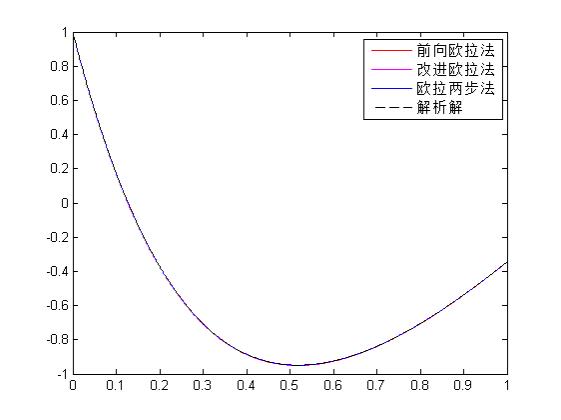
当n=100时，三种方法与解析解非常接近，当n=1000时，几乎四者位于一条线中，从实验结果看出，n越大时，结果越精确。