算法导论 practice3
Posted olive_gyr
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了算法导论 practice3相关的知识,希望对你有一定的参考价值。
1. 0-1 knapsack problem
Instance : weight capacity is 100
|
item |
weights |
values |
|
A |
50 |
200 |
|
B |
30 |
180 |
|
C |
45 |
225 |
|
D |
25 |
200 |
|
E |
5 |
50 |
0-1背包问题有最优子结构、重叠子问题————用动态规划。
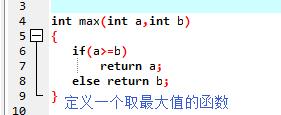
I的值是---装了几个物品
J的值是---现在背包的容量
存的元素---现在的价值
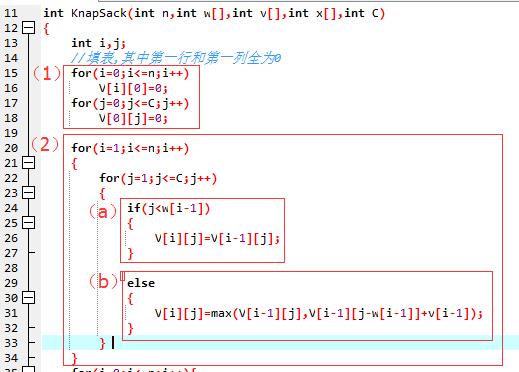
令V(i,j)表示在前i(1<=i<=n)个物品中能够装入容量为j(1<=j<=C)的背包中的物品的最大价值,则可以得到如下的动态规划函数:
(1) V(i,0)=V(0,j)=0
(2) V(i,j)=V(i-1,j) j<wi
V(i,j)=max{V(i-1,j) ,V(i-1,j-wi)+vi) } j>wi
(1)式表明:如果第i个物品的重量大于背包的容量,则装入前i个物品得到的最大价值和装入前i-1个物品得到的最大价是相同的,即物品i不能装入背包;
(2)式表明:如果第i个物品的重量小于背包的容量,则会有一下两种情况:
(a)如果第i个物品没有装入背包,则背包中物品价值就等于把前i-1个物品装入容量为j的背包中所取得的价值。
(b)如果把第i个物品装入背包,则背包物品的价值等于第i-1个物品装入容量位j-wi 的背包中的价值加上第i个物品的价值vi;
显然,取二者中价值最大的作为把前i个物品装入容量为j的背包中的最优解。
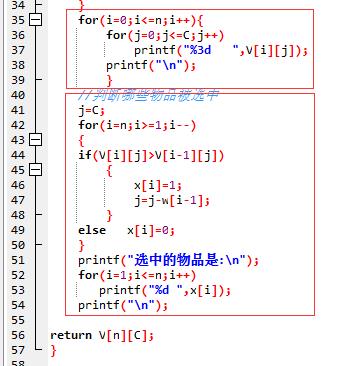
打印出当前的v数组和被选中物品的x数组:
在主函数中调用KnapSack函数:

运行结果如下:
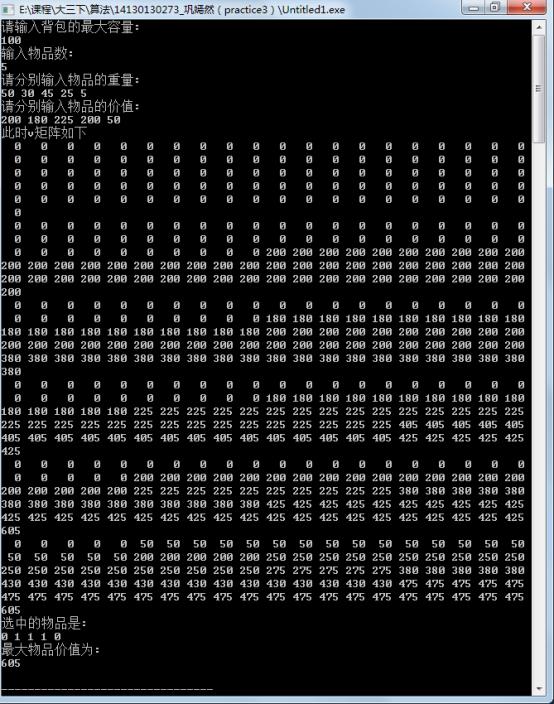
1 2 #include<stdio.h> 3 int V[200][200];//前i个物品装入容量为j的背包中获得的最大价值 4 5 int max(int a,int b) 6 { 7 if(a>=b) 8 return a; 9 else return b; 10 } 11 12 int KnapSack(int n,int w[],int v[],int x[],int C) 13 { 14 int i,j; 15 //填表,其中第一行和第一列全为0 16 for(i=0;i<=n;i++) 17 V[i][0]=0; 18 for(j=0;j<=C;j++) 19 V[0][j]=0; 20 21 for(i=1;i<=n;i++) 22 { 23 for(j=1;j<=C;j++) 24 { 25 if(j<w[i-1]) 26 { 27 V[i][j]=V[i-1][j]; 28 } 29 30 else 31 { 32 V[i][j]=max(V[i-1][j],V[i-1][j-w[i-1]]+v[i-1]); 33 } 34 } 35 } 36 for(i=0;i<=n;i++){ 37 for(j=0;j<=C;j++) 38 printf("%3d ",V[i][j]); 39 printf("\\n"); 40 } 41 //判断哪些物品被选中 42 j=C; 43 for(i=n;i>=1;i--) 44 { 45 if(V[i][j]>V[i-1][j]) 46 { 47 x[i]=1; 48 j=j-w[i-1]; 49 } 50 else x[i]=0; 51 } 52 printf("选中的物品是:\\n"); 53 for(i=1;i<=n;i++) 54 printf("%d ",x[i]); 55 printf("\\n"); 56 57 return V[n][C]; 58 } 59 60 int main() 61 { 62 int s;//获得的最大价值 63 int w[15];//物品的重量 64 int v[15];//物品的价值 65 int x[15];//物品的选取状态 66 int n,i; 67 int C;//背包最大容量 68 n=5; 69 printf("请输入背包的最大容量:\\n"); 70 scanf("%d",&C); 71 72 printf("输入物品数:\\n"); 73 scanf("%d",&n); 74 printf("请分别输入物品的重量:\\n"); 75 for(i=0;i<n;i++) 76 scanf("%d",&w[i]); 77 78 printf("请分别输入物品的价值:\\n"); 79 for(i=0;i<n;i++) 80 scanf("%d",&v[i]); 81 printf("此时v矩阵如下\\n"); 82 s=KnapSack(n,w,v,x,C); 83 84 printf("最大物品价值为:\\n"); 85 printf("%d\\n",s); 86 87 88 }
2. Fractional knapsack problem
Instance: same as 1
部分背包问题具有贪心性选择,最优子结构----用贪心算法
Part1:
(1)在主函数中输入已知信息(背包最大容量、物品数、物品重量、物品价值),根据已知计算出单位重量的价值,放在a数组。(2)调用快速排序算法,把单位重量的价值按增序排列放在aver数组中。(3)调用greedy函数。

Part2:
普通快速排序算法
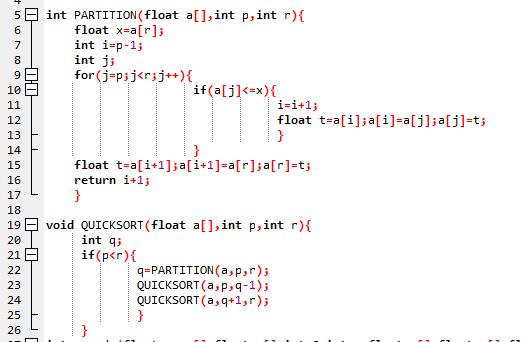
Part3:
(1)构造并输出二维数组b数组。第一行:单位重量的价值增序;第二行:对应的重量;第三行:对应的价值。(2)构造并输出x数组贪心性选择是单位重量的价值最大的。(3)根据b和x数组计算最大价值s并输出。
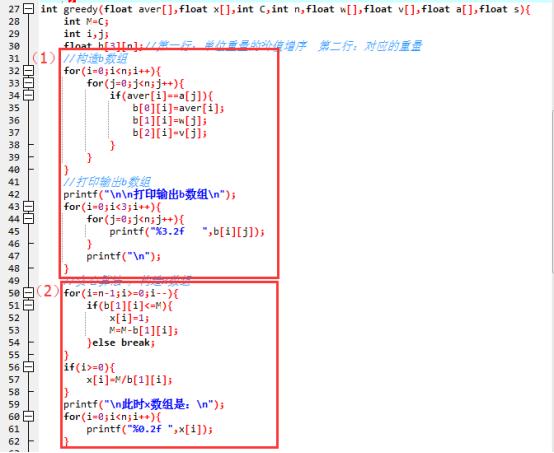

运行结果如下:
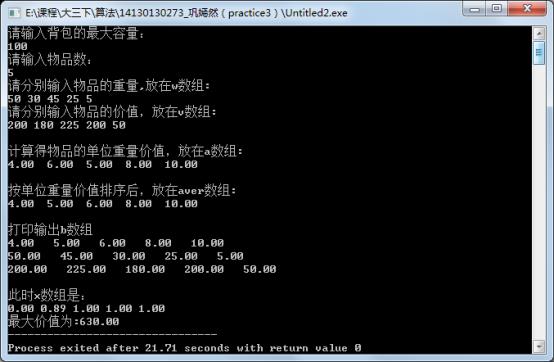
1 #include<stdio.h> 2 #include<stdlib.h> 3 4 int PARTITION(float a[],int p,int r){ 5 float x=a[r]; 6 int i=p-1; 7 int j; 8 for(j=p;j<r;j++){ 9 if(a[j]<=x){ 10 i=i+1; 11 float t=a[i];a[i]=a[j];a[j]=t; 12 } 13 } 14 float t=a[i+1];a[i+1]=a[r];a[r]=t; 15 return i+1; 16 } 17 18 void QUICKSORT(float a[],int p,int r){ 19 int q; 20 if(p<r){ 21 q=PARTITION(a,p,r); 22 QUICKSORT(a,p,q-1); 23 QUICKSORT(a,q+1,r); 24 } 25 } 26 int greedy(float aver[],float x[],int C,int n,float w[],float v[],float a[],float s){ 27 int M=C; 28 int i,j; 29 float b[3][n];//第一行:单位重量的价值增序 第二行:对应的重量 30 //构造b数组 31 for(i=0;i<n;i++){ 32 for(j=0;j<n;j++){ 33 if(aver[i]==a[j]){ 34 b[0][i]=aver[i]; 35 b[1][i]=w[j]; 36 b[2][i]=v[j]; 37 } 38 } 39 } 40 //打印输出b数组 41 printf("\\n\\n打印输出b数组\\n"); 42 for(i=0;i<3;i++){ 43 for(j=0;j<n;j++){ 44 printf("%3.2f ",b[i][j]); 45 } 46 printf("\\n"); 47 } 48 //贪心算法 ,构造x数组 49 for(i=n-1;i>=0;i--){ 50 if(b[1][i]<=M){ 51 x[i]=1; 52 M=M-b[1][i]; 53 }else break; 54 } 55 if(i>=0){ 56 x[i]=M/b[1][i]; 57 } 58 printf("\\n此时x数组是:\\n"); 59 for(i=0;i<n;i++){ 60 printf("%0.2f ",x[i]); 61 } 62 63 for(i=0;i<n;i++){ 64 s+=x[i]*b[2][i]; 65 } 66 printf("\\n最大价值为:%0.2f",s); 67 } 68 69 int main(){ 70 float s=0;//获得的最大价值 71 float w[15];//物品重量; 72 float v[15];//物品价值; 73 float a[15];//单位重量的价值 74 float aver[15];//寸排序后的 单位重量的价值 75 float x[15];//物品的选取状态 76 int C;//背包的最大容量 77 int n;//物品数 78 int i; 79 80 printf("请输入背包的最大容量:\\n"); 81 scanf("%d",&C); 82 printf("请输入物品数:\\n"); 83 scanf("%d",&n); 84 for(i=0;i<n;i++){//初始化x数组 85 x[i]=0; 86 } 87 printf("请分别输入物品的重量,放在w数组:\\n"); 88 for(i=0;i<n;i++) 89 scanf("%f",&w[i]); 90 printf("请分别输入物品的价值,放在v数组:\\n"); 91 for(i=0;i<n;i++) 92 scanf("%f",&v[i]); 93 printf("\\n计算得物品的单位重量价值,放在a数组:\\n"); 94 for(i=0;i<n;i++){ 95 a[i]=v[i]/w[i]; 96 aver[i]=v[i]/w[i]; 97 printf("%0.2f ",a[i]); 98 } 99 100 printf("\\n\\n按单位重量价值排序后,放在aver数组:\\n"); 101 QUICKSORT(aver,0,n-1); 102 for(i=0;i<n;i++){ 103 printf("%0.2f ",aver[i]); 104 } 105 106 greedy(aver,x,C,n,w,v,a,s); 107 }
3. A simple scheduling problem. We are given jobs j1, j2… jn, all with known running time t1, t2… tn, respectively. We have a single processor. What is the best way to schedule these jobs in order to minimize the average completion time. Assume that it is a non-preemptive scheduling: once a job is started, it must run to completion. The following are some instances:
(j1, j2, j3, j4) : (15,8,3,10)
我理解的completion time:finish time – arrive time
题目默认所有arrive time都是0 。
贪心性选择是:维持时间最短的作业。
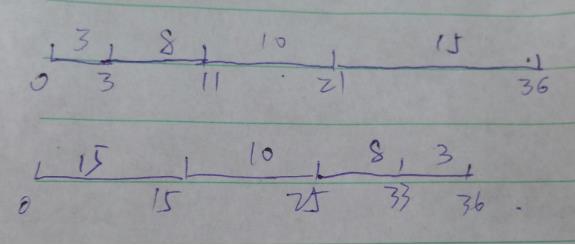
(1) 调用快速排序,将作业时间按增序排好在数组a中
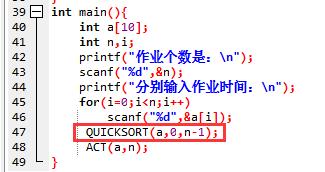
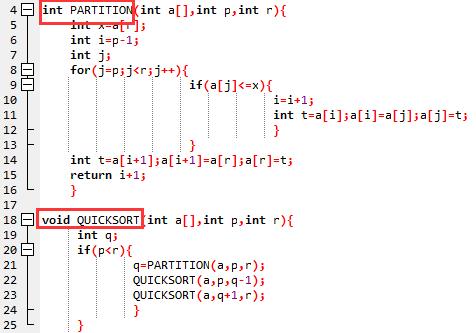
(2) 调用ACT函数:
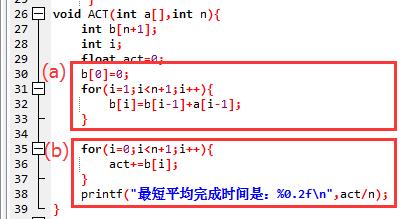
(a)创建数组b,存放按最短作业优先方案时,作业完成的时间。
(b)最短平均完成时间就是b数组的和除以个数。
运行结果是:
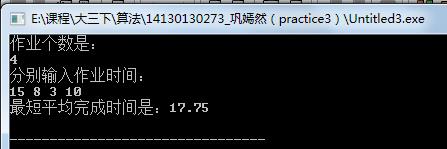
4. Bin Packing: We have a number of bins each with a capacity of 1, and we have a set of objects all with different seizes, s1,s2,…,sn between 0 and 1. What is the fewest number of bins that would be needed to store all of the objects?
Instance: 0.5,0.7,0.3,0.9,0.6,0.8,0.1,0.4,0.2,0.5
Part1:
(1)调用void QUICKSORT(float a[],int p,int r)将different seizes按增序排列,存在数组a中。
(2)求出最少需要的箱子数n(除不尽时用进一)。
(3)调用BinPacking。
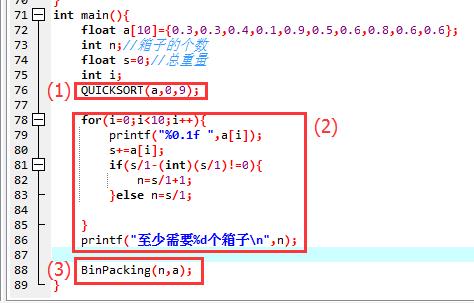
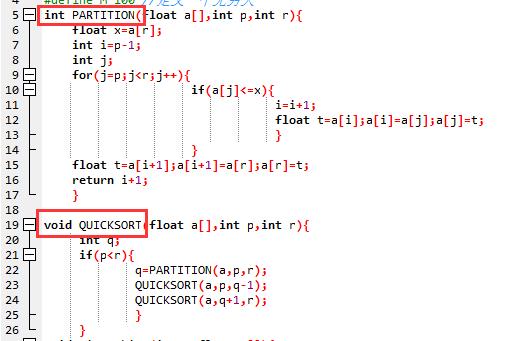
Part2:(写BinPacking函数)
(1)创建数组二维b,第i行表示第i个箱子装的size。创建数组free,第i个数据表示第i行还可以装多少。初始化数组free和b。
(2)从后向前遍历a数组,用k控制下标。用i,j控制下标,按行考虑能不能把a数组中的数字填进去(标准是free[i])。
(3)打印出遍历完的数组。
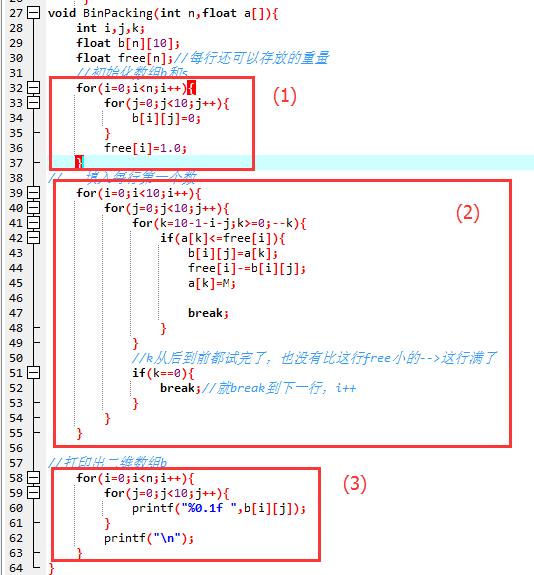
运行结果如下:
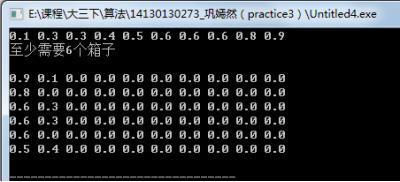
#include<stdio.h> #include<stdlib.h> #define M 100 //定义一个无穷大 int PARTITION(float a[],int p,int r){ float x=a[r]; int i=p-1; int j; for(j=p;j<r;j++){ if(a[j]<=x){ i=i+1; float t=a[i];a[i]=a[j];a[j]=t; } } float t=a[i+1];a[i+1]=a[r];a[r]=t; return i+1; } void QUICKSORT(float a[],int p,int r){ int q; if(p<r){ q=PARTITION(a,p,r); QUICKSORT(a,p,q-1); QUICKSORT(a,q+1,r); } } void BinPacking(int n,float a[]){ int i,j,k; float b[n][10]; float free[n];//每行还可以存放的重量 //初始化数组b和s for(i=0;i<n;i++){ for(j=0;j<10;j++){ b[i][j]=0; } free[i]=1.0; } // 填入每行第一个数 for(i=0;i<10;i++){ for(j=0;j<10;j++){ for(k=10-1-i-j;k>=0;--k){ if(a[k]<=free[i]){ b[i][j]=a[k]; free[i]-=b[i][j]; a[k]=M; break; } } //k从后到前都试完了,也没有比这行free小的-->这行满了 if(k==0){ break;//就break到下一行,i++ } } } //打印出二维数组b for(i=0;i<n;i++){ for(j=0;j<10;j++){ printf("%0.1f ",b[i][j]); } printf("\\n"); } } int main(){ float a[10]={0.3,0.3,0.4,0.1,0.9,0.5,0.6,0.8,0.6,0.6}; int n;//箱子的个数 float s=0;//总重量 int i; QUICKSORT(a,0,9); for(i=0;i<10;i++){ printf("%0.1f ",a[i]); s+=a[i]; if(s/1-(int)(s/1)!=0){ n=s/1+1; }else n=s/1; } printf("\\n至少需要%d个箱子\\n\\n",n); BinPacking(n,a); }
以上是关于算法导论 practice3的主要内容,如果未能解决你的问题,请参考以下文章