数据结构-图-经典算法

Posted 2020-06-21 LC凑热闹

参考资料

http://blog.csdn.net/weinierbian/article/details/8059129

http://www.cnblogs.com/biyeymyhjob/archive/2012/07/30/2615542.html

百度百科

一、最小生成树算法

给定一个带权的无向连通图,如何选取一棵生成树,使树上所有边上权的总和为最小,这叫最小生成树.

常见的两种算法是：Kruskal算法、Prim算法 

Kruskal算法简述

假设 WN=(V,{E}) 是一个含有 n 个顶点的连通网，则按照克鲁斯卡尔算法构造最小生成树的过程为：先构造一个只含 n 个顶点，而边集为空的子图，若将该子图中各个顶点看成是各棵树上的根结点，则它是一个含有 n 棵树的一个森林。之后，从网的边集 E 中选取一条权值最小的边，若该条边的两个顶点分属不同的树，则将其加入子图，也就是说，将这两个顶点分别所在的两棵树合成一棵树；反之，若该条边的两个顶点已落在同一棵树上，则不可取，而应该取下一条权值最小的边再试之。依次类推，直至森林中只有一棵树，也即子图中含有 n-1条边为止。

Prim算法简述

1).输入：一个加权连通图，其中顶点集合为V，边集合为E；

2).初始化：Vnew= {x}，其中x为集合V中的任一节点（起始点），Enew= {},为空；

3).重复下列操作，直到Vnew= V：

a.在集合E中选取权值最小的边<u, v>，其中u为集合Vnew中的元素，而v不在Vnew集合当中，并且v∈V（如果存在有多条满足前述条件即具有相同权值的边，则可任意选取其中之一）；

b.将v加入集合Vnew中，将<u, v>边加入集合Enew中；

4).输出：使用集合Vnew和Enew来描述所得到的最小生成树。

 

两种算法复杂度对比：

Kruskal：克鲁斯卡尔算法需要对图的边进行访问，所以克鲁斯卡尔算法的时间复杂度只和边又关系，可以证明其时间复杂度为O（eloge）。

Prim ：该算法的时间复杂度为O(n²)。与图中边数无关，该算法适合于稠密图

图例：

Kruskal算法

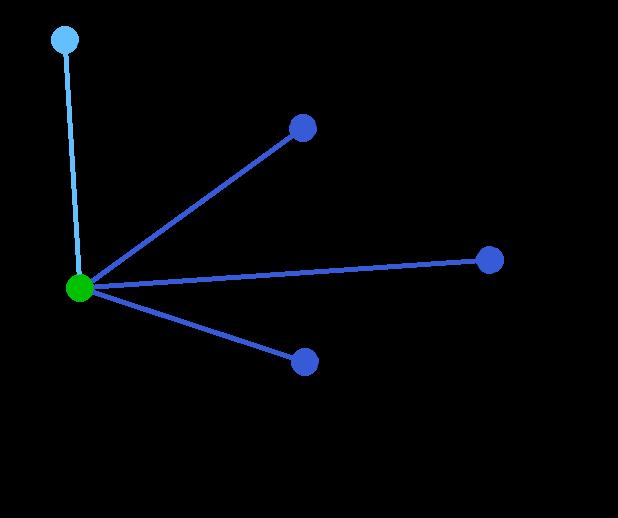
首先第一步，我们有一张图Graph，有若干点和边 

 

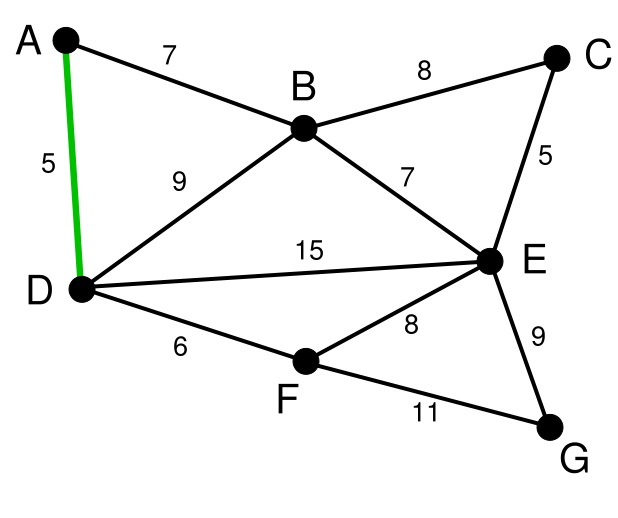
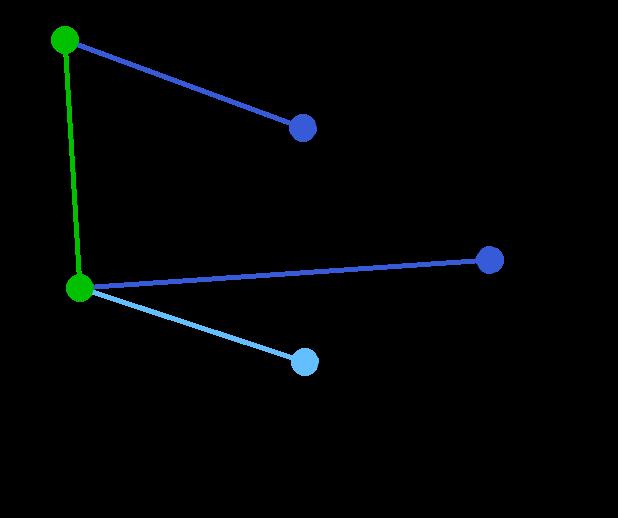
将所有的边的长度排序，用排序的结果作为我们选择边的依据。这里再次体现了贪心算法的思想。资源排序，对局部最优的资源进行选择，排序完成后，我们率先选择了边AD。这样我们的图就变成了右图

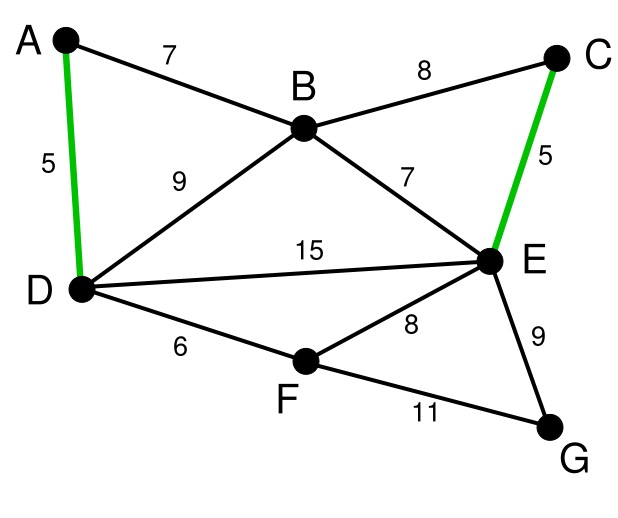
在剩下的变中寻找。我们找到了CE。这里边的权重也是5

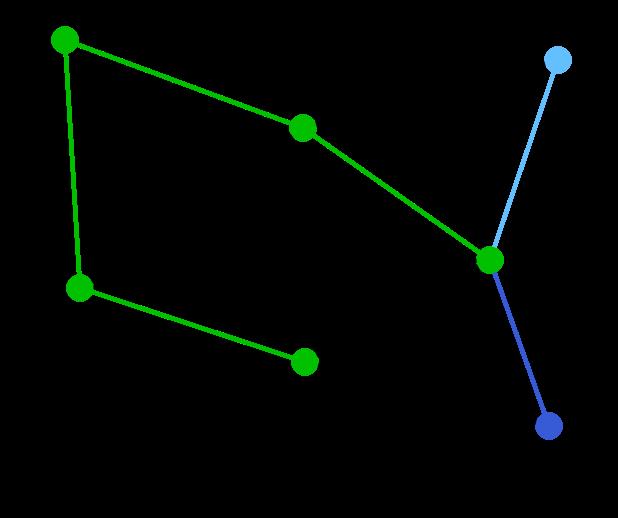
依次类推我们找到了6,7,7，即DF，AB，BE。

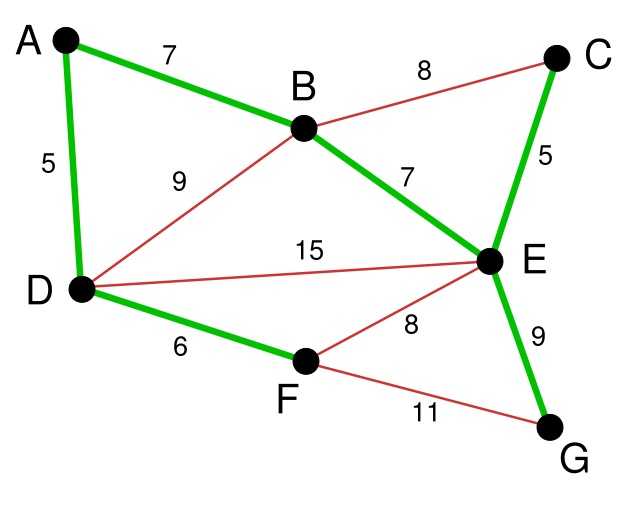
下面继续选择， BC或者EF尽管现在长度为8的边是最小的未选择的边。但是现在他们已经连通了（对于BC可以通过CE,EB来连接，类似的EF可以通过EB,BA,AD,DF来接连）。所以不需要选择他们。类似的BD也已经连通了（这里上图的连通线用红色表示了）。

最后就剩下EG和FG了。当然我们选择了EG。

 

Prim算法：

图例	说明	不可选	可选	已选（Vnew）
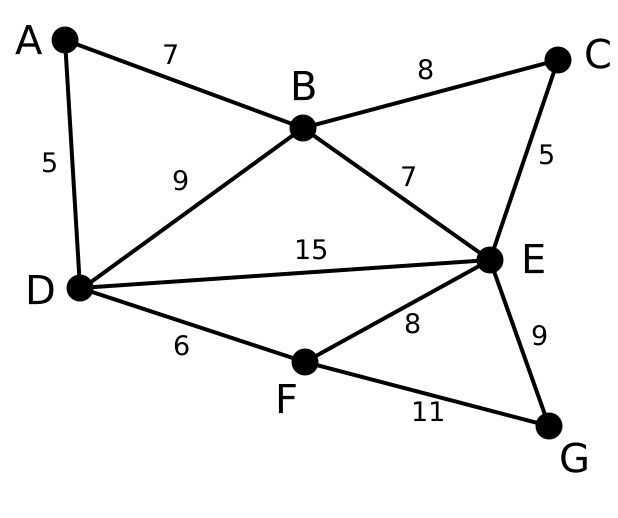
	此为原始的加权连通图。每条边一侧的数字代表其权值。	-	-	-
	顶点D被任意选为起始点。顶点A、B、E和F通过单条边与D相连。A是距离D最近的顶点，因此将A及对应边AD以高亮表示。	C, G	A, B, E, F	D
	下一个顶点为距离D或A最近的顶点。B距D为9，距A为7，E为15，F为6。因此，F距D或A最近，因此将顶点F与相应边DF以高亮表示。	C, G	B, E, F	A, D
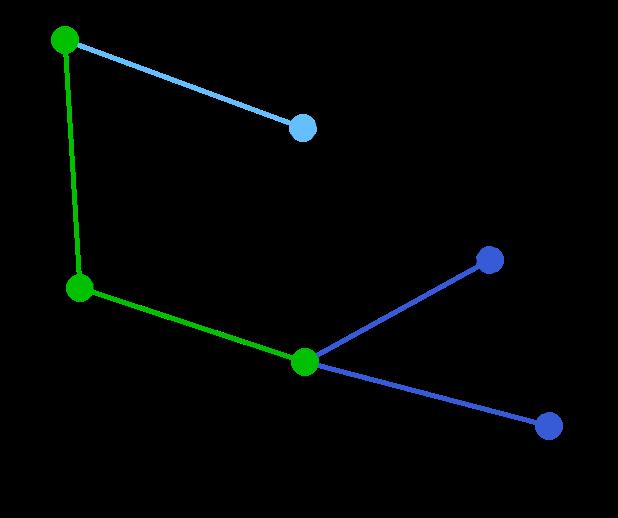	算法继续重复上面的步骤。距离A为7的顶点B被高亮表示。	C	B, E, G	A, D, F
	在当前情况下，可以在C、E与G间进行选择。C距B为8，E距B为7，G距F为11。E最近，因此将顶点E与相应边BE高亮表示。	无	C, E, G	A, D, F, B
	这里，可供选择的顶点只有C和G。C距E为5，G距E为9，故选取C，并与边EC一同高亮表示。	无	C, G	A, D, F, B, E
	顶点G是唯一剩下的顶点，它距F为11，距E为9，E最近，故高亮表示G及相应边EG。	无	G	A, D, F, B, E, C
	现在，所有顶点均已被选取，图中绿色部分即为连通图的最小生成树。在此例中，最小生成树的权值之和为39。	无	无	A, D, F, B, E, C, G

 

实现代码：

Kruskal

 1 typedef struct          
 2 {        
 3     char vertex[VertexNum];                                //顶点表         
 4     int edges[VertexNum][VertexNum];                       //邻接矩阵,可看做边表         
 5     int n,e;                                               //图中当前的顶点数和边数         
 6 }MGraph; 
 7  
 8 typedef struct node  
 9 {  
10     int u;                                                 //边的起始顶点   
11     int v;                                                 //边的终止顶点   
12     int w;                                                 //边的权值   
13 }Edge; 
14 
15 void kruskal(MGraph G)  
16 {  
17     int i,j,u1,v1,sn1,sn2,k;  
18     int vset[VertexNum];                                    //辅助数组，判定两个顶点是否连通   
19     int E[EdgeNum];                                         //存放所有的边   
20     k=0;                                                    //E数组的下标从0开始   
21     for (i=0;i<G.n;i++)  
22     {  
23         for (j=0;j<G.n;j++)  
24         {  
25             if (G.edges[i][j]!=0 && G.edges[i][j]!=INF)  
26             {  
27                 E[k].u=i;  
28                 E[k].v=j;  
29                 E[k].w=G.edges[i][j];  
30                 k++;  
31             }  
32         }  
33     }     
34     heapsort(E,k,sizeof(E[0]));                            //堆排序，按权值从小到大排列       
35     for (i=0;i<G.n;i++)                                    //初始化辅助数组   
36     {  
37         vset[i]=i;  
38     }  
39     k=1;                                                   //生成的边数，最后要刚好为总边数   
40     j=0;                                                   //E中的下标   
41     while (k<G.n)  
42     {   
43         sn1=vset[E[j].u];  
44         sn2=vset[E[j].v];                                  //得到两顶点属于的集合编号   
45         if (sn1!=sn2)                                      //不在同一集合编号内的话，把边加入最小生成树   
46         {
47             printf("%d ---> %d, %d",E[j].u,E[j].v,E[j].w);       
48             k++;  
49             for (i=0;i<G.n;i++)  
50             {  
51                 if (vset[i]==sn2)  
52                 {  
53                     vset[i]=sn1;  
54                 }  
55             }             
56         }  
57         j++;  
58     }  
59 }