Your current task is to make a ground plan for a residential building located in HZXJHS. So you must determine a way to split the floor building with walls to make apartments in the shape of a rectangle. Each built wall must be paralled to the building‘s sides.
The floor is represented in the ground plan as a large rectangle with dimensions
,
where each apartment is a smaller rectangle with dimensions
located
inside. For each apartment, its dimensions can be different from each other. The number
and
must
be integers.
Additionally, the apartments must completely cover the floor without one
square
located on
.
The apartments must not intersect, but they can touch.
For this example, this is a sample of
.
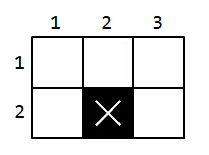
To prevent darkness indoors, the apartments must have windows. Therefore, each apartment must share its at least one side with the edge of the rectangle representing the floor so it is possible to place a window.
Your boss XXY wants to minimize the maximum areas of all apartments, now it‘s your turn to tell him the answer.
For each testcase, print only one interger, representing the answer.
1
2
Hint
Case 1 :
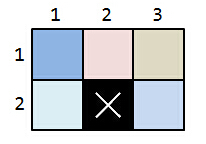
You can split the floor into five
apartments. The answer is 1.
Case 2:
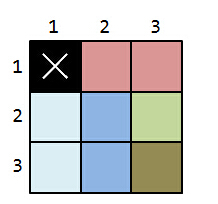
You can split the floor into three
apartments and two
apartments. The answer is 2.
If you want to split the floor into eight
apartments, it will be unacceptable because the apartment located on (2,2) can‘t have windows.
解题思路:
假设没有不合法的块,那结果就是长和宽中最小值的一半,而,不合法的块所影响的仅仅有它周围的四块,计算出这四块距离四个边的距离的最小值,就是加入上不合法块之后该块所须要的最长距离。
须要注意特判一中情况。即不合法块在正中间的时候,并不造成影响。
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <algorithm>
using namespace std;
int n, m, x, y;
int main()
{
while(scanf("%d%d%d%d", &n, &m, &x, &y)!=EOF)
{
if(n == m && (n % 2 == 1 && m % 2 == 1) && (x == y && x == (n+1)/2))
{
cout << (n -1) / 2 << endl;
continue;
}
int Min = min(n, m); int ans;
if(Min & 1) ans = (Min + 1) / 2;
else ans = Min / 2;
int res = -10;
int xx = x - 1, yy = y;
if(xx >= 1 && yy >= 1) res = max(res, min(xx-1,min(yy-1,m-yy)));
xx = x, yy = y-1;
if(xx >= 1 && yy >= 1) res = max(res, min(min(xx-1,n-xx),yy-1));
xx = x + 1, yy = y;
if(xx <=n && yy >= 1) res = max(res, min(n-xx,min(yy-1,m-yy)));
xx = x, yy = y+1;
if(xx >= 1 && yy <= m) res = max(res, min(min(xx-1,n-xx),m-yy));
res += 1;
ans = max(ans, res);
printf("%d\n", ans);
}
return 0;
}