[noip 2015]运输计划 [LCA][树链剖分]

Posted 2020-09-19 ZYBGMZL

用了luogu上的题目描述

题目背景

公元 2044 年,人类进入了宇宙纪元。

题目描述

L 国有 n 个星球,还有 n-1 条双向航道,每条航道建立在两个星球之间,这 n-1 条航道连通了 L 国的所有星球。

小 P 掌管一家物流公司,该公司有很多个运输计划,每个运输计划形如:有一艘物

流飞船需要从 ui 号星球沿最快的宇航路径飞行到 vi 号星球去。显然,飞船驶过一条航道 是需要时间的,对于航道 j,任意飞船驶过它所花费的时间为 tj,并且任意两艘飞船之 间不会产生任何干扰。

为了鼓励科技创新,L 国国王同意小 P 的物流公司参与 L 国的航道建设,即允许小 P 把某一条航道改造成虫洞,飞船驶过虫洞不消耗时间。

在虫洞的建设完成前小 P 的物流公司就预接了 m 个运输计划。在虫洞建设完成后, 这 m 个运输计划会同时开始,所有飞船一起出发。当这 m 个运输计划都完成时,小 P 的 物流公司的阶段性工作就完成了。

如果小 P 可以自由选择将哪一条航道改造成虫洞,试求出小 P 的物流公司完成阶段 性工作所需要的最短时间是多少?

输入输出格式

输入格式：

输入文件名为 transport.in。

第一行包括两个正整数 n、m,表示 L 国中星球的数量及小 P 公司预接的运输计划的数量,星球从 1 到 n 编号。

接下来 n-1 行描述航道的建设情况,其中第 i 行包含三个整数 ai, bi 和 ti,表示第

i 条双向航道修建在 ai 与 bi 两个星球之间,任意飞船驶过它所花费的时间为 ti。

接下来 m 行描述运输计划的情况,其中第 j 行包含两个正整数 uj 和 vj,表示第 j个 运输计划是从 uj 号星球飞往 vj 号星球。

输出格式：

输出 共1行,包含1个整数,表示小P的物流公司完成阶段性工作所需要的最短时间。

输入输出样例

输入样例#1：

6 3 
1 2 3 
1 6 4 
3 1 7 
4 3 6 
3 5 5 
3 6 
2 5 
4 5

输出样例#1：

11

说明

 

---

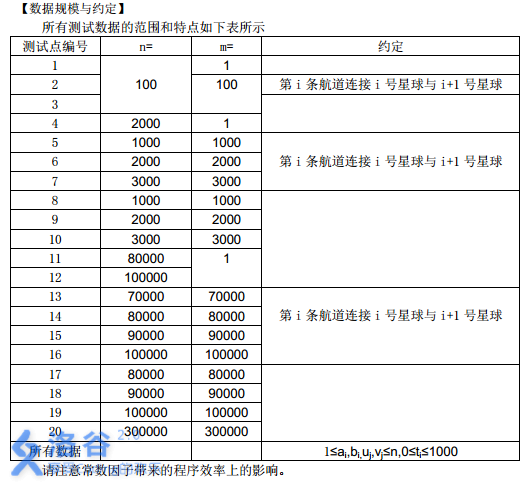
  1 #include<cstdio>
  2 #include<algorithm>
  3 #include<cstring>
  4 using namespace std;
  5 
  6 struct range {
  7     int x,y,len;
  8     bool operator < (const range &n1) const {
  9         return len>n1.len;
 10     }
 11 };
 12 
 13 const int maxn=300001;
 14 
 15 int root,n,m,x,y,tot,next[maxn],last[maxn],e[maxn],dep[maxn],fa[maxn],size[maxn],son[maxn],top[maxn],pos[maxn];
 16 int pos2[maxn],val[maxn],cost[maxn],MAX[maxn],dist[maxn],s[maxn],node,ans,q[maxn];
 17 range d[maxn];
 18 
 19 inline int read()
 20 {
 21     char ch;
 22     int re=0;
 23     bool flag=0;
 24     while((ch=getchar())!=‘-‘&&(ch<‘0‘||ch>‘9‘));
 25     ch==‘-‘?flag=1:re=ch-‘0‘;
 26     while((ch=getchar())>=‘0‘&&ch<=‘9‘)  re=(re<<1)+(re<<3)+ch-‘0‘;
 27     return flag?-re:re;
 28 }
 29 
 30 void add(int x,int y,int v)
 31 {
 32     next[++tot]=last[x];
 33     last[x]=tot;
 34     val[tot]=v;
 35     e[tot]=y;
 36 }
 37 
 38 void dfs1(int x)
 39 {
 40     dep[x]=dep[fa[x]]+1;
 41     size[x]=1;
 42     for (int i=last[x];i;i=next[i])
 43     {
 44         int v=e[i];
 45         if (v==fa[x])continue;
 46         fa[v]=x;
 47         dist[v]=dist[x]+val[i];
 48         cost[v]=val[i];
 49         dfs1(v);
 50         size[x]+=size[v];
 51         if (size[v]>size[son[x]])son[x]=v;
 52     }
 53 }
 54 
 55 void dfs2(int x,int tp)
 56 {
 57     top[x]=tp;pos[x]=++node;pos2[node]=cost[x];
 58     if (son[x]==0)return;
 59     dfs2(son[x],tp);
 60     for (int i=last[x];i;i=next[i])
 61     {
 62         int v=e[i];
 63         if (v==fa[x]||v==son[x])continue;
 64         dfs2(v,v);
 65     }
 66 }
 67 
 68 int query(int x,int y)
 69 {
 70     int a=x,b=y;
 71     while (top[a]!=top[b])
 72     {
 73         if (dep[top[a]]<dep[top[b]])std::swap(a,b);
 74         a=fa[top[a]];
 75     }
 76     if (dep[a]<dep[b])return a;else return b;
 77 } 
 78 
 79 void work(int x,int y)
 80 {
 81     int a=x,b=y;
 82     while (top[a]!=top[b])
 83     {
 84         if (dep[top[a]]<dep[top[b]])std::swap(a,b);
 85         s[pos[top[a]]]+=1;s[pos[a]+1]-=1;
 86         a=fa[top[a]];
 87     }
 88     if (a==b)return;
 89     if (dep[a]>dep[b]) std::swap(a,b);
 90     s[pos[a]+1]+=1;s[pos[b]+1]-=1;;
 91 } 
 92 
 93 int check(int mid)
 94 {
 95     int sz=0;
 96     while (d[sz+1].len>mid)sz++;
 97     if (q[sz]!=0)  return q[sz];
 98     std::memset(s,0,sizeof(s));
 99     for (int i=1;i<=sz;i++)work(d[i].x,d[i].y);
100     int Maxx=0,tott=0;
101     for (int i=1;i<=n;i++)  {tott+=s[i];if (tott==(sz))Maxx=std::max(Maxx,pos2[i]);}
102     q[sz]=Maxx;
103     return Maxx;
104 }
105 
106 int main()
107 {
108     //freopen("temp.in","r",stdin);
109     n=read();m=read();
110     for (int i=1;i<n;i++){
111         int v;
112         x=read();y=read();v=read();
113         add(y,x,v);add(x,y,v);
114     }
115     dfs1(1);
116     dfs2(1,1);
117     
118     for (int i=1;i<=m;i++){
119         d[i].x=read();d[i].y=read();
120         d[i].len=dist[d[i].x]+dist[d[i].y]-2*dist[query(d[i].x,d[i].y)];
121     }
122     
123     sort(d+1,d+1+m);
124     
125     int l=0,r=d[1].len;
126     while (l<=r)
127     {
128         int mid=(l+r)>>1;
129         if (d[1].len-check(mid)>mid)
130         {
131             l=mid+1;
132         }else r=mid-1,ans=mid;
133     }
134     
135     printf("%d\n",ans);
136     
137     return 0;    
138 }

萎靡不振

---

你说害怕别人看见它 应该把它们撕碎吧