查找算法

Posted 2020-09-19 段子手实习生

讲解之前我们先讲一个概念——符号表

符号表的最主要作用就是把一个键和一个值联系起来。

我们会使用符号表这个词来描述一张抽象的表格。我们会将信息（值）存在其中，然后按照指定的键来搜索并获取这些信息。

符号表有时被称为字典。就像是一步字典，键是词，值是释义。

符号表有时又叫索引。数组就是索引结构，键即索引，值即数组中的元素。

所有的实现要遵循以下规则：

　　1.每个键只对应一个值（表中不允许存在重复的键）。

　　2.当用例代码向表中存入的键值对和表中已有的键（及关联值）冲突时，新的值会替代旧的值。

1.无序链表查找

我们把所有的元素用一个无序的链表进行存储起来。每一个节点记录key值，value值以及指向下一个记录的对象。

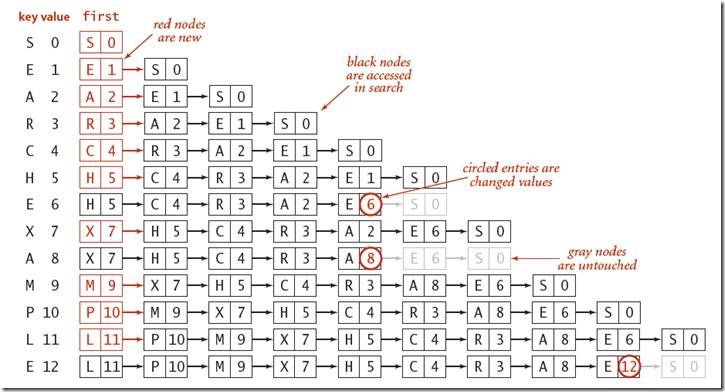
如图，当我们往链表中插入元素的时候，从表头开始查找，如果找到，则更新value，否则，在表头插入新的节点元素。

无序链表的插入和查找的*均时间复杂度均为O(n)。

2.二分查找

和采用无序链表实现不同，二分查找的思想是在内部维护一个按照key排好序的二维数组，每一次查找的时候，跟中间元素进行比较，如果该元素小，则继续左半部分递归查找，否则继续右半部分递归查找。

 

采用二分查找只需要最多lgN+1次的比较即可找到对应元素，所以查找效率比较高。

但是对于插入元素来说，每一次插入不存在的元素，需要将该元素放到指定的位置，然后，将他后面的元素依次后移，所以*均时间复杂度O(n)，对于插入来说效率仍然比较低。

3.二叉查找树

 

二叉查找树（Binary Search Tree），也称有序二叉树（ordered binary tree）,排序二叉树（sorted binary tree），是指一棵空树或者具有下列性质的二叉树：

1. 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

2. 若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

3. 任意节点的左、右子树也分别为二叉查找树。

4. 没有键值相等的节点（no duplicate nodes）。

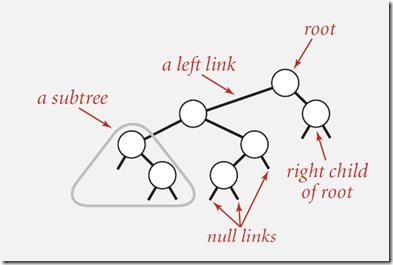
如下图，这个是普通的二叉树：

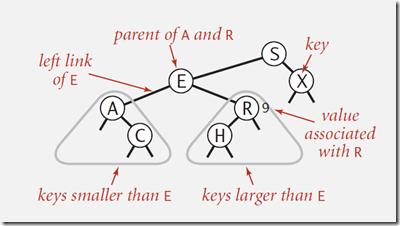
在此基础上，加上节点之间的大小关系，就是二叉查找树：

数据表示：一个键，一个值，一个左链接，一个右链接，一个节点计数器。

使用二叉查找树的算法的运行时间取决于树的形状，而树的形状又取决于键被插入的先后顺序。在最好的情况下，一颗含有N个节点的树是完全*衡的。我们假设我们的键都是（均匀）随机的。对这个模型来说，二叉查找树和快速排序几乎就是“双胞胎”。树的根节点就是快速排序中的第一个切分元素（左侧的键都 比它小，右侧的键都比它大），而这对于所有的子树都同样适用。这和快速排序中对子数组的递归排序完全一对应。

二叉树的增加、修改和查找操作都比较容易，比较难的是二叉树的删除操作。删除操作要保证树的有序性。

T.Hibbard在1962年提出第一个方法：在删除节点x后用它的后继节点填补它的位置。

删除步骤

　　1. 保存带删除的节点到临时变量t

　　2. 将t的右节点的最小节点min(t.right)保存到临时节点x

　　3. 将x的右节点设置为deleteMin(t.right)，该右节点是删除后，所有比x.key最大的节点。

　　4. 将x的左节点设置为t的左节点。

 

范围查找:

　　要实现能够返回给定范围内键的keys()方法，我们首先需要一个遍历二叉树的基本方法——中序遍历——将所有所在给定范围以内的键都加入一个队列中，并跳过那些不可能含有所查找键的子树。

4.*衡二叉树

因为二叉查找树的形状依赖于输入顺序，当树的深度过大的时候，会造成性能的降低，极端情况下，树就变成了链表。为了避免树的高度增长过快，我们规定在插入和删除二叉树节点时，要保证任一节点的左右子树的高度差的绝对值不能超过1，讲这样的二叉树叫做*衡二叉树（AVL树）。定义节点的左子树和右子树的高度差为该节点的*衡因子，则*衡二叉树的*衡因子只有-1,1和0。

算法思想：

　　每当在二叉排序树中插入（或删除）一个节点时，首先要检查其插入路径上的节点是否因为此次操作而导致了不*衡。如果导致了不*衡，则先找到插入路径上离插入节点最*的*衡因子绝对值大于1的节点A，然后对A为根的子树金习性调整，来达到*衡。——每次调整的都是最小不*衡子树。

具体可以分为四种情况：LL*衡旋转，RR*衡旋转，LR*衡旋转，RL*衡旋转。（具体的可以参考《王道》）

5.*衡查找树

对于*衡二叉查找树，在动态插入中要保持树的完美*衡的代价实在太高了。这里我们稍稍放松完美*衡的要求。

5.1 2-3查找树

和二叉树不一样，2-3树运行每个节点保存1个或者两个的值。对于普通的2节点(2-node)，他保存1个key和左右两个子节点的指针。对应3节点(3-node)，保存两个Key，2-3查找树的定义如下：

1. 要么为空，要么：

2. 对于2节点，该节点保存一个key及对应value，以及两个指向左右节点的节点，左节点也是一个2-3节点，所有的值都比key小，右节点也是一个2-3节点，所有的值比key要大。

3. 对于3节点，该节点保存两个key及对应value，以及三个指向左中右的节点。左节点也是一个2-3节点，所有的值均比两个key中的最小的key还要小；中间节点也是一个2-3节点，中间节点的key值在两个跟节点key值之间；右节点也是一个2-3节点，节点的所有key值比两个key中的最大的key还要大。

如果中序遍历2-3查找树，就可以得到排好序的序列。在一个完全*衡的2-3查找树中，根节点到每一个为空节点的距离都相同。

插入节点：

　　2-3查找树和二叉树不同，它的生长方式是从下往上增长的，插入节点的时候要插入到底部节点内，如果底部节点时2-node则不变，如果是3-node，则表示里边有两个节点，这时插入后，把中间节点提升到父节点中，左右节点分别作为它的左右节点。如果父节点是2-node则不变，如果是3-node的话， 需要继续往上传递，直到最后，如果根节点也往上传递了，则此时树的高度增加1。

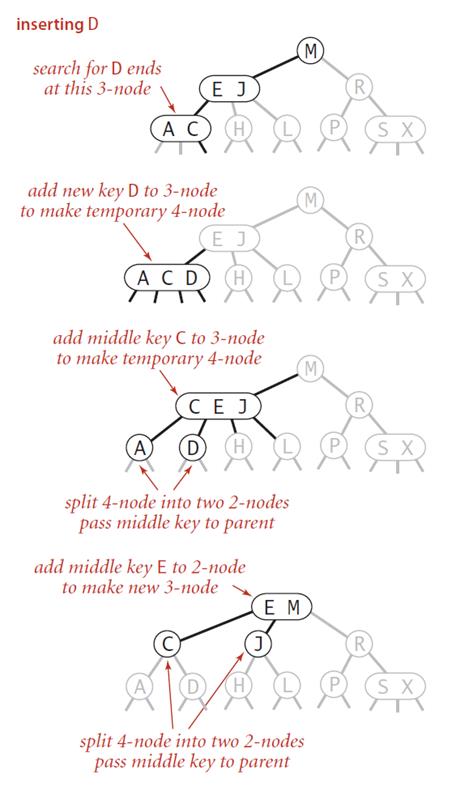
2-3查找树在最坏的情况下依然可以保持很好的性能。每个操作中处理每个节点的时间都不会超过一个很小的常数。在含有10亿个节点的一颗2-3查找树的高度仅在19到30之间。我们最多只需要访问30个节点就可以在10亿个键中进行任意查找插入操作。

但是2-3查找树实现起来很麻烦：

1. 需要处理不同的节点类型，非常繁琐
2. 需要多次比较操作来将节点下移
3. 需要上移来拆分4-node节点
4. 拆分4-node节点的情况有很多种

2-3查找树实现起来比较复杂，在某些情况插入后的*衡操作可能会使得效率降低。在2-3查找树基础上改进的红黑树不仅具有较高的效率，并且实现起来较2-3查找树简单。

5.2 红黑树

直接实现2-3查找树比较麻烦，我们选择使用红黑树来实现2-3查找树。

红黑二叉树背后的基本思想是用标准二叉查找树（完全由2-节点构成）和一些额外的信息（替换3-节点）来表示2-3树。我们将树中的链接分为两种类型：红链接将两个2-节点连起来构成一个3-节点，黑链接则是2-3树中的普通链接。确切的说，我们将3-节点表示为一条左斜的红色链接（两个2-节点其中之一是另一个的左节点）相连的两个2-节点。我们这样做的优点是：我们无需修改就可以直接使用标准二叉查找树的查找方法。

对于任意2-3查找树，只要对节点进行转换，我们都可以立即派生出一颗对应的二叉查找树，我们称之为红黑二叉查找树。

根据以上描述，红黑树定义如下：

红黑树是一种具有红色和黑色链接的*衡查找树，同时满足：

• 红色节点向左倾斜
• 一个节点不可能有两个红色链接
• 整个书完全黑色*衡，即从根节点到所以叶子结点的路径上，黑色链接的个数都相同。

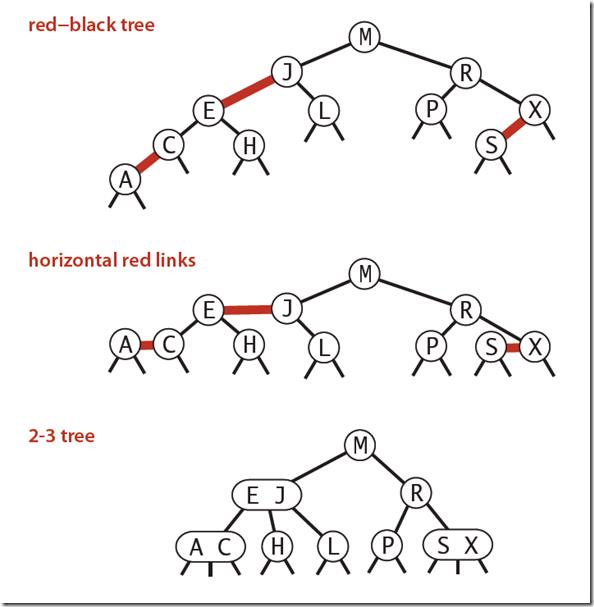
下图可以看到红黑树其实是2-3树的另外一种表现形式：如果我们将红色的连线水*绘制，那么他链接的两个2-node节点就是2-3树中的一个3-node节点了。

 

红黑树的插入和删除操作依然比较复杂，具体的可以参考其他的博客和课本。

在最坏的情况下，红黑树的高度不超过2lgN

最坏的情况就是，红黑树中除了最左侧路径全部是由3-node节点组成，即红黑相间的路径长度是全黑路径长度的2倍。

下图是一个典型的红黑树，从中可以看到最长的路径(红黑相间的路径)是最短路径的2倍：

红黑树的*均高度大约为lgN

红黑树接*完美*衡的，它能够保证对数级别的查找和插入操作。

6.B/B+树

1970年，R.Bayer和E.mccreight提出了一种适用于外查找的树，它是一种*衡的多叉树，称为B树（或B-树、B_树）。

B/B+树是为了磁盘或其它存储设备而设计的一种*衡多路查找树(相对于二叉,B树每个内节点有多个分支),与红黑树相比,在相同的的节点的情况下,一颗B/B+树的高度远远小于红黑树的高度。B/B+树上操作的时间通常由存取磁盘的时间和CPU计算时间这两部分构成,而CPU的速度非常快,所以B树的操作效率取决于访问磁盘的次数,关键字总数相同的情况下B树的高度越小，磁盘I/O所花的时间越少。

 

B树的性质

 

• 定义任意非叶子结点最多只有M个儿子；且M>2；
• 根结点的儿子数为[2, M]；
• 除根结点以外的非叶子结点的儿子数为[M/2, M]；
• 每个结点存放至少M/2-1（取上整）和至多M-1个关键字；（至少2个关键字）
• 非叶子结点的关键字个数=指向儿子的指针个数-1；
• 非叶子结点的关键字：K[1], K[2], …, K[M-1]；且K[i] < K[i+1]；
• 非叶子结点的指针：P[1], P[2], …, P[M]；其中P[1]指向关键字小于K[1]的子树，P[M]指向关键字大于K[M-1]的子树，其它P[i]指向关键字属于(K[i-1], K[i])的子树；
• 所有叶子结点位于同一层； 
  
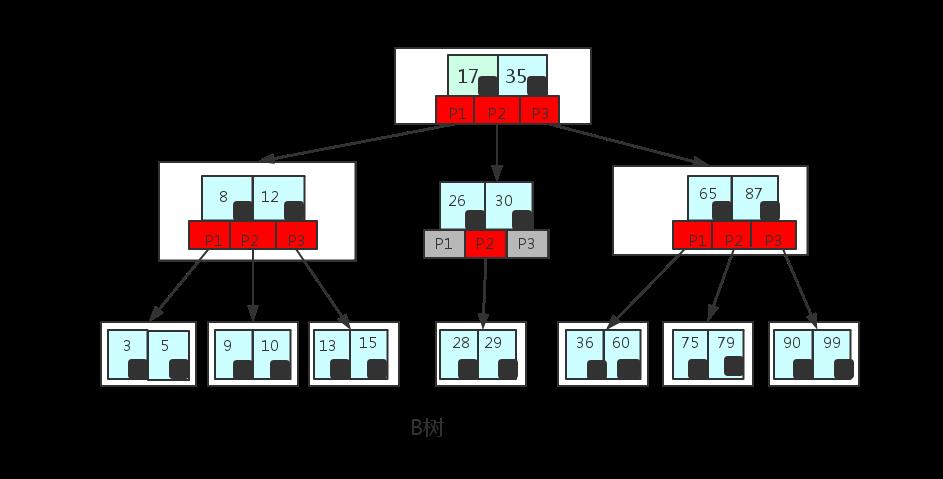
  这里只是一个简单的B树,在实际中B树节点中关键字很多的.上面的图中比如35节点,35代表一个key(索引)，而小黑块代表的是这个key所指向的内容在内存中实际的存储位置.是一个指针.

B+树

B+树是应文件系统所需而产生的一种B树的变形树(文件的目录一级一级索引,只有最底层的叶子节点(文件)保存数据.),非叶子节点只保存索引,不保存实际的数据,数据都保存在叶子节点中.这不就是文件系统文件的查找吗?我们就举个文件查找的例子:有3个文件夹,a,b,c, a包含b,b包含c,一个文件yang.c, a,b,c就是索引(存储在非叶子节点), a,b,c只是要找到的yang.c的key,而实际的数据yang.c存储在叶子节点上. 
所有的非叶子节点都可以看成索引部分

B+树的性质(下面提到的都是和B树不相同的性质)

• 非叶子节点的子树指针与关键字个数相同;
• 非叶子节点的子树指针p[i],指向关键字值属于[k[i],k[i+1]]的子树.(B树是开区间,也就是说B树不允许关键字重复,B+树允许重复)；
• 为所有叶子节点增加一个链指针.
• 所有关键字都在叶子节点出现(稠密索引). (且链表中的关键字恰好是有序的);
• 非叶子节点相当于是叶子节点的索引(稀疏索引),叶子节点相当于是存储(关键字)数据的数据层.
• 更适合于文件系统; 
  看下图: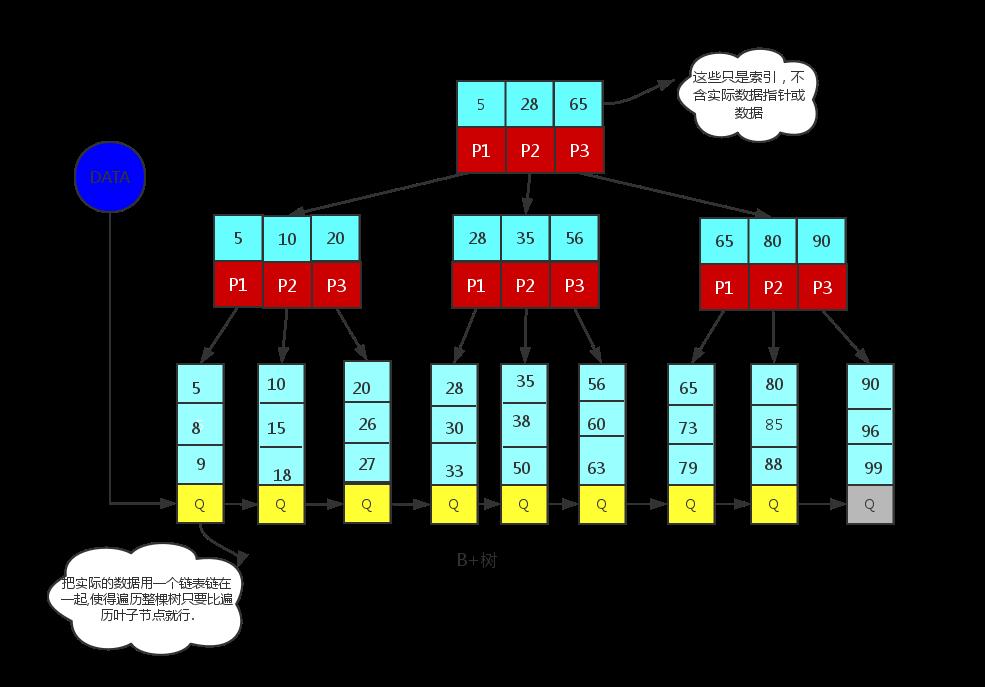 
   
  非叶子节点(比如5,28,65)只是一个key(索引),实际的数据存在叶子节点上(5,8,9)才是真正的数据或指向真实数据的指针.

应用　　

B和B+树主要用在文件系统以及数据库做索引.比如mysql;

B/B+树性能分析　

• n个节点的*衡二叉树的高度为H(即logn),而n个节点的B/B+树的高度为logt((n+1)/2)+1; 　　
• 若要作为内存中的查找表,B树却不一定比*衡二叉树好,尤其当m较大时更是如此.因为查找操作CPU的时间在B-树上是O(mlogtn)=O(lgn(m/lgt)),而m/lgt>1;所以m较大时O(mlogtn)比*衡二叉树的操作时间大得多. 因此在内存中使用B树必须取较小的m.（通常取最小值m=3，此时B-树中每个内部结点可以有2或3个孩子，这种3阶的B-树称为2-3树）。

为什么说B+tree比B树更适合实际应用中操作系统的文件索引和数据索引？　

• B+-tree的内部节点并没有指向关键字具体信息的指针,因此其内部节点相对B树更小,如果把所有同一内部节点的关键字存放在同一盘块中,那么盘块所能容纳的关键字数量也越多,一次性读入内存的需要查找的关键字也就越多,相对IO读写次数就降低了.
• 由于非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。 
  ps:我在知乎上看到有人是这样说的,我感觉说的也挺有道理的: 
  他们认为数据库索引采用B+树的主要原因是:B树在提高了IO性能的同时并没有解决元素遍历的我效率低下的问题,正是为了解决这个问题,B+树应用而生.B+树只需要去遍历叶子节点就可以实现整棵树的遍历.而且在数据库中基于范围的查询是非常频繁的，而B树不支持这样的操作（或者说效率太低）.　

 

 

7.散列表

 如果所有的键都是小整数，我们可用一个数组来实现无序的符号表，将键作为数组的索引而数组中键i处存储的就是它对应的值。这样我们就可以快速访问任意键的值。

但是这个方法有局限性：当键的范围特别的广，数组会很稀疏，造成浪费。而且只适合处理整数。

这里我们将这个方法扩展成能够处理更加复杂的类型的键——散列表

 

散列表连个步骤：

　　1.用散列函数将被查找的键转化为数组的一个索引。理想情况下，不同的键都能转换成不同的索引值。

　　2.处理碰撞冲突（拉链法和线性探测法）

散列函数和键的类型有关。严格的说，对于每种类型的键我们都需要一个与之对应的散列函数。如果是一个数，比如社会保险号，我们就可以直接使用这个数；如果键是一个字符串，比如一个人的名字，我们就需要将这个字符串转化成一个数；如果键包含很多部分，比如邮件地址，我们需要使用某些方法将这些部分组合起来。

正整数使用最常见的是除留余数法。我们选择大小为素数M的数组，对于任意正整数K，计算K除以M的余数。

为什么要选择素数？

　　如果M不是素数，我们可能无法利用键中包含的所有信息，这可能导致我们无法均匀的散列散列值。例如键是十进制而M为10的幂，那么我们只能利用键的后k位，这可能会导致一些问题。如下图所示：

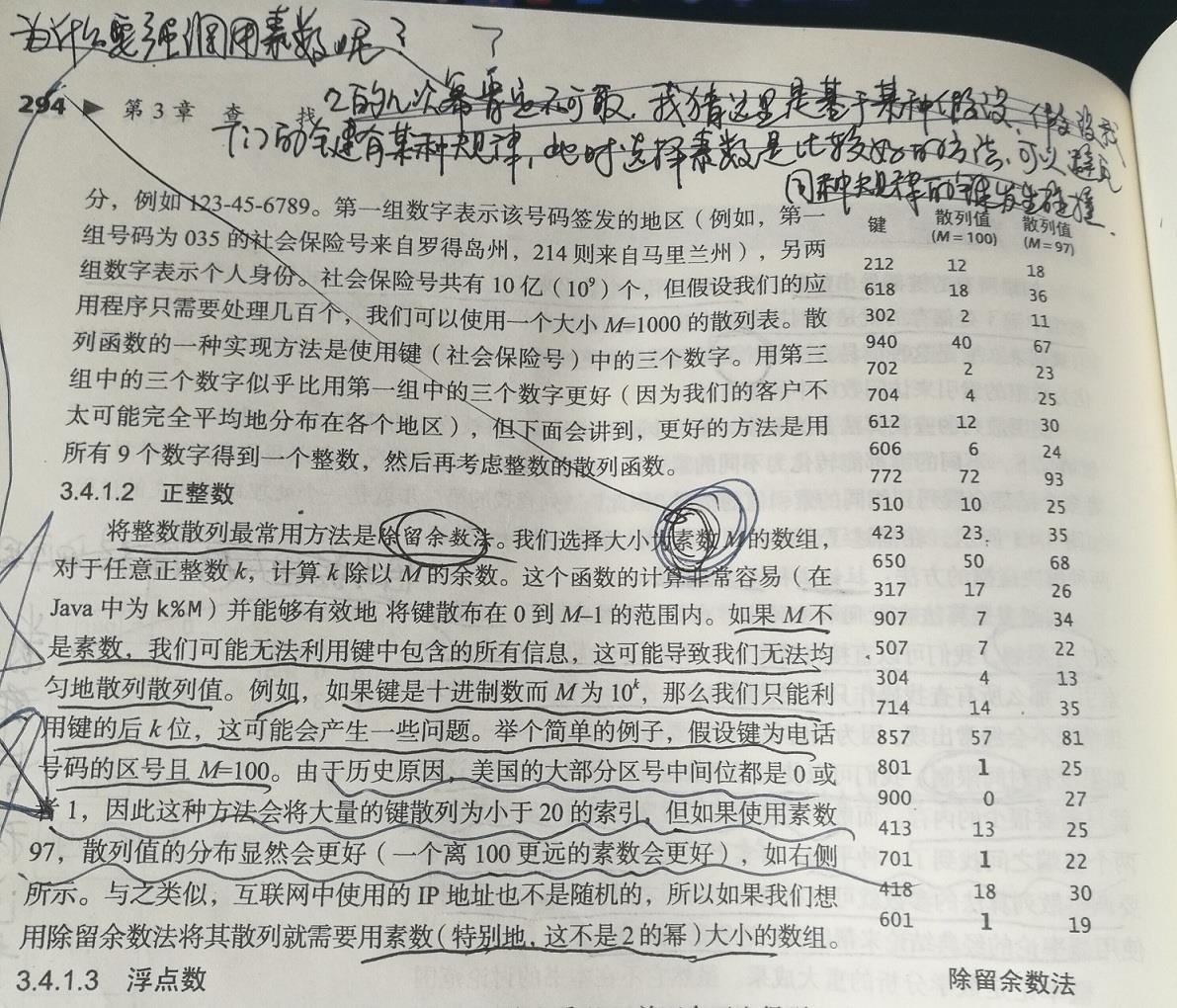
我们是基于某种假设——我们的键具有某种规律，而不是随机的，此时选择素数是规避风险的一种好的方法。

 

基于拉链法的散列表的实现简单。在键的顺序并不重要的应用中，它可能是最快的（也是使用最广泛的）符号表实现。

基于拉链的散列表可以直接删除元素，而基于线性探测的散列表删除元素后，要将簇中被删除键的右侧的所有键都重新插入散列表。

线性探测的性能取决于元素在插入数组后聚集成的一组连续的条目，也叫键簇。短小键簇才能保证较高的效率。

符号表的缺陷：

1.每种类型的键都需要一个优秀的散列函数；

2.性能保证来自于散列函数的质量；

3.散列函数的计算可能复杂而且昂贵；

4.难以支持有序性相关的符号表操作。

 

总结：

猜测：

2-3查找树是B树的一种特殊形式吗？

题

　　1.海量数据——给定a，b两个文件，各存放了50亿个url，每个url各占64字节，内存限制是4G，让你找出a，b文件共同的url？

解：可以估计每个文件的大小为5G*64=320G，远远大于内存限制的4G，所以不可能将其完全加载到内存中处理，考虑采取分而治之的办法。

　　①hash映射：遍历文件a，对每一个url求取，然后根据所得的值将url分别存储到1000个小文件中，这样每个小文件大小为300M，遍历文件b，采取a相同的方式将url分别存储到1000个小文件中，这样处理之后，所有可能的url都在对应的小文件中，我们只要求出1000对小文件中相同的url即可。

　　②hash_set统计：求每队小文件中相同的url时，可以把其中一个小文件存储到hash_set中，然后遍历另一个小文件的每个url，看其中是否存在刚才构建的hash_set中，然后遍历另一个小文件中的每个url，看其是否存在刚才构建的hash_set中，如果是，那么就是共同的url。

 

 

参考：http://m.blog.csdn.net/article/details?id=51926985

　　　http://www.cnblogs.com/yangecnu/p/Introduce-Symbol-Table-and-Elementary-Implementations.html

　　　《算法 第四版》

　　　《王道 联考复习指导》