数据结构与算法系列研究四——数组和广义表
Posted 精心出精品
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构与算法系列研究四——数组和广义表相关的知识,希望对你有一定的参考价值。
稀疏矩阵的十字链表实现和转置
一、数组和广义表的定义
数组的定义1:一个 N 维数组是受 N 组线性关系约束的线性表。
二维数组的逻辑结构可形式地描述为:
2_ARRAY(D,R)
其中 D={aij} | i=0,1,...,b1-1; j=0,1,...,b2-1;aij∈D0}
R={Row,Col}
Row={<aij,ai,j+1>|0<=i<=b1-1;0<=j<=b2-2;aij,ai,j+1∈D0}
ai,j+1是aij在行关系中的后继元素。
Col={<aij,ai+1,j>|0<=i<=b1-2;0<=j<=b2-1;aij,ai+1,j∈D0}
ai+1,j是aij在列关系中的后继元素。
①每一个数组元素a[i][j]都受两个关系Row和Col的约束:
ROW(行关系):ai,j+1 是aij在行关系中的直接后继。
COL(列关系):ai+1,j是aij在列关系中的后继元素。
②每个数组元素属于同一数据类型。
③每个数组元素由下标(i,j)唯一确定其位置。
④每个下标i由bi限定其范围,0≤i≤bi-1
n维数组的逻辑结构可描述为:
n_ARRAY(D,R)
D---数组的元素
R---定义为数组元素间的关系
R=(R1,R2,...,Rn)
数组的定义2 :一维数组是定长线性表; 二维数组是一个定长线性表,它的每个元素是一个一维数组;n维数组是线性表,它的每个元素是n-1维数组。
数组是线性结构,基于两点:
1、一个 n维数组被定义为一个线性表,它的元素是一个 n-1维数组。
2、一个 n维数组的数据元素受n个关系的约束,且每个关系都是线性的。


![]()

![]()
其中: cn =L, ci-1= bi × ci, 1<i ≤ n ; ci 为常数
上式称为n维数组的存储映象函数
数组的基本操作:
1、数组初始化:确定数组维数、长度,分配存储空间。
initarray(&A,n,bound[ ]);
bound[ ]= b1,b2......bn
2、撤消数组
destroyarray (&A);
3、求数组元素值
value(A,&e,index[ ]);
index[ ]= i1,i2,......in
4、为数组元素赋值
assign(&A,e,index[ ]);
数组的顺序表示及实现:
用一遍地址连续的存储单元依次存放数据元素。
1、数据类型描述
#define MAX_ARRAY_DIM 8
typedef struct {
ElemType *base; //数组元素空间
int dim; //数组维数
int *bounds; //数组维长
int *constant; //常数因子
}ARRAY;
矩阵的压缩存储:
1、矩阵压缩存储的概念
特殊矩阵:值相同元素或0元素在矩阵中分布有一定规律。
⒈对称矩阵:矩阵中的元素满足
aij=aji 1≤i,j≤n
⒉三角矩阵:上(下)三角矩阵指矩阵的下(上)三角(不包括对角线)中的元素均为常数c或0的n阶矩阵。
⒊对角矩阵(带状矩阵):矩阵中所有非0元素集中在以主对角线为中心的区域中。
稀疏矩阵:非0元素很少( ≤ 5%)且分布无规律。
2、矩阵的压缩存储
为多个相同值的元分配一个存储单元;对零元不分配空间。
对称矩阵的压缩存储
存储分配策略: 每一对对称元只分配一个存储单元,即只存储下三角(包括对角线)的元, 所需空间数为:
n×(n+1)/2。
存储分配方法: 用一维数组sa[n(n+1)/2]作为存储结构。
sa[k]与aij之间的对应关系为:
稀疏矩阵存储分配策略
只存储稀疏矩阵的非0元素。
矩阵中的一个元素可以用行列下标和其值来唯一表示,因此可以用一个三元组(i,j,aij) 唯一确定一个非0元素。
逻辑上,用三元组表来表示稀疏矩阵的非0元
广义表的定义
广义表又称为列表(lists),是n≥0个元素a1,a2,...,an的有限序列,记为:
A=( a1,a2,...,an)
其中:
A是广义表的表名,n是广义表的长度
ai 是单个元素或广义表,
若ai是单个元素,则称为广义表的单元素(或原子)。
若是广义表,则称ai是广义表的子表。所以广义表又称为列表。
即 ai ∈D0 或 ai ∈lists
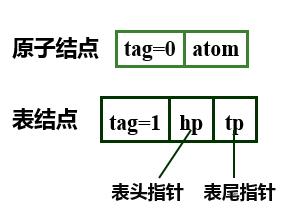
广义表的表头(Head):非空表A 的第一个元素 a1。
广义表的头与a1具有相同的表示形式。
广义表的表尾(Tail):除其头之外的其余元素( a2,...,an)组成的表。
广义表的尾一定是一个广义表。
特点:广义表的定义是一个递归的定义。

二、稀疏矩阵的十字链表实现
2.1.实验内容
编程实现稀疏矩阵的十字链表实现
1.用txt文件录入稀疏矩阵数组,格式如下:
m n t //表示行号,列号和总数
i j value
..................
2.读文件建立十字链表
3.输出建立后的链表,格式为;
行号1 列号11 值** 列号12 值*** 。。。。。
行号2 列号21 值** 列号22 值*** 。。。。。
。。。。。。。。。
4.实现矩阵的转置
5.输出转置后的矩阵,格式为矩阵形式。
2.2.输入和输出
输入:本程序采取文件读写形式,文件中数值格式详见实验内容
输出:本程序有两种输出形式分别为按行输出和按矩阵形式输出
2.3.关键数据结构与算法描述
数据结构:建立十字链表需要知道行列号i,j和链表的right,down指针,以及节点的数值,于是数据结构呼之欲出,又因过程中读文件时需要先建立一个缓冲器存储节点的信息, 则两个结构具体如下:

/***********以下构建数据结构************/
typedef struct OLink{
int i,j;
ElemType value;
struct OLink *right,*down;
}*LinkList,OLink;
/************构建存储结构*************/
typedef struct record{
int i;
int j;
int value;
}RECORD;
/**************构建完毕**************/
算法描述:
建立十字链表,
1.首先要知道链表的头节点,因每行,每列都需要一个循环链表,则共需要m+n+1个头指针,m个行指针,n个列指针,1个总头指针。
2.建立完两个指针链表之后(注意:此处链表的每一个元素都是附加头节点),就要对矩阵的元素进行插入,当插入元素时要注意和对应行,对应列都建立联系,构成网状结构,当插入完元素之后,十字链表也就建立完毕了。
3.余下的就是输出元素了,根据头节点共有两种输出方法,一种按行输出,一种按列输出。当然也可以把非零元素放到二维数组中,通过二维数组进行输出。
4.最后,就是矩阵的转置,只需将a[i][j]与a[j][i]交换即可,再重新建立十字链表,修改初始化和i,j指向即可。其中最核心的算法就是头节点的构建和元素的插入了,具体代码如下:

/*************创建行,列头节点*****************/
void CreateHead(LinkList *head, int m, int n)
{
//以下建立列头结点
LinkList p = *head,q;
//构建列头节点
for(int i=0; i<n; i++)
{
q = (LinkList)malloc(sizeof(OLink));
q->i = -1; //注意在矩阵的外面,也可以不赋值
q->j = i; //代表矩阵的列号,从0开始
q->down = q; //构建循环链表的标志
p->right = q; //链接
p = q; //继续向前推进
}
p->right = (*head);//循环链表的标志
//以下建立行头结点,基本原理同上
p = (*head);
for(i=0; i<m; i++)
{
q = (LinkList)malloc(sizeof(OLink));
q->i = i;
q->j = -1;
q->right = q;
p->down = q;
p = q;
}
p->down = (*head);
}
/************各个头节点构建完毕,共m+n+1个************/
/***************插入节点的算法************************/
bool InsertNode(LinkList *head, int i, int j, ElemType e)
{
LinkList p = *head,q;
if(i < 0||j < 0||i >= (*head)->i||j >= (*head)->j)
return false;
/********构建节点********/
q = (LinkList)malloc(sizeof(OLink));
q->i = i;
q->j = j;
q->value = e;
/*******完毕***********/
for(int k=0; k<=i; k++)
{
p = p->down;//注意此处等于i截至
}
//产生定位指针
LinkList sr = p,s = p->right;
/******若不满足s==p,或者插入元素大于后面元素,继续推进********/
while(s!=p && q->j>s->j)
{
sr = s;
s=s -> right;
}
/*******推进完毕,有可能有三种情况*************/
q->right = s;
sr->right = q;
/**********行链接处理完毕*********************/
/******以下链接列链表,方法同上**********************/
p = *head;
for( k=0; k<=j; k++)
{
p = p->right;
}
sr = p;
s = p->down;
while(s!=p && q->j>s->j)
{
sr = s;
s = s->down;
}
q->down = s;
sr->down = q;
/**********列链接处理完毕*********************/
return true;
}
2.4.测试与理论
1.在文件操作中输入如下文本: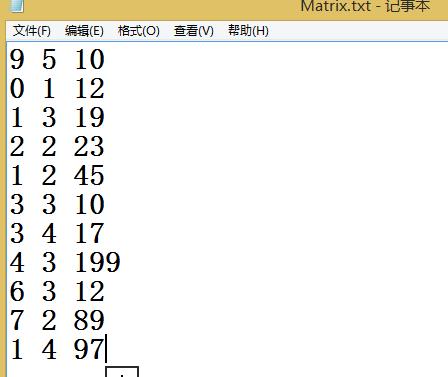
2.程序运行后应产生9*5的矩阵,具体输出形式应与要求一致,如图;

3.转置后变成5*9的矩阵,具体显示如下
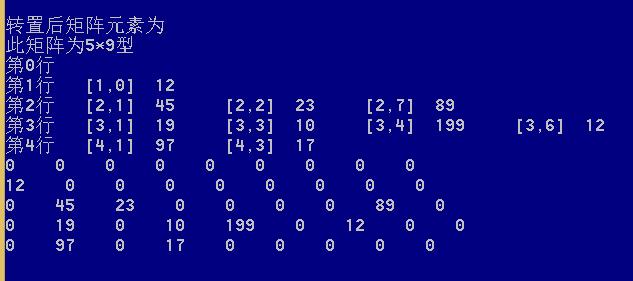
2.5、所有程序

1 #include "stdlib.h"
2 #include "conio.h"
3 #include "iostream"
4 using namespace std;
5
6 typedef int ElemType;//设置元素类型
7
8 /***********以下构建数据结构************/
9 typedef struct OLink{
10 int i,j;
11 ElemType value;
12 struct OLink *right,*down;
13 }*LinkList,OLink;
14 /************构建存储结构*************/
15 typedef struct record{
16 int i;
17 int j;
18 int value;
19 }RECORD;
20 /**************构建完毕**************/
21
22 /**************进行初始化操作********************/
23 void InitArray(LinkList *head, int m, int n)
24 {
25 *head = (LinkList)malloc(sizeof(OLink));
26 (*head)->i=m; //行长度
27 (*head)->j=n; //列长度
28 }
29 /***************初始化完毕*********************/
30
31 /*************创建行,列头节点*****************/
32 void CreateHead(LinkList *head, int m, int n)
33 {
34 //以下建立列头结点
35 LinkList p = *head,q;
36 //构建列头节点
37 for(int i=0; i<n; i++)
38 {
39 q = (LinkList)malloc(sizeof(OLink));
40 q->i = -1; //注意在矩阵的外面,也可以不赋值
41 q->j = i; //代表矩阵的列号,从0开始
42
43 q->down = q; //构建循环链表的标志
44 p->right = q; //链接
45 p = q; //继续向前推进
46 }
47 p->right = (*head);//循环链表的标志
48
49 //以下建立行头结点,基本原理同上
50 p = (*head);
51 for(i=0; i<m; i++)
52 {
53 q = (LinkList)malloc(sizeof(OLink));
54 q->i = i;
55 q->j = -1;
56
57 q->right = q;
58 p->down = q;
59 p = q;
60 }
61 p->down = (*head);
62 }
63 /************各个头指针构建完毕,共m+n+1个************/
64
65 /***************插入节点的算法************************/
66 bool InsertNode(LinkList *head, int i, int j, ElemType e)
67 {
68 LinkList p = *head,q;
69 if(i < 0||j < 0||i >= (*head)->i||j >= (*head)->j)
70 return false;
71
72 /********构建节点********/
73 q = (LinkList)malloc(sizeof(OLink));
74 q->i = i;
75 q->j = j;
76 q->value = e;
77 /*******完毕***********/
78
79
80 for(int k=0; k<=i; k++)
81 {
82 p = p->down;//注意此处等于i截至
83 }
84 //产生定位指针
85 LinkList sr = p,s = p->right;
86 /******若不满足s==p,或者插入元素大于后面元素,继续推进********/
87 while(s!=p && q->j>s->j)
88 {
89 sr = s;
90 s=s -> right;
91 }
92 /*******推进完毕,有可能有三种情况*************/
93 q->right = s;
94 sr->right = q;
95 /**********行链接处理完毕*********************/
96
97
98 /******以下链接列链表,方法同上**********************/
99 p = *head;
100 for( k=0; k<=j; k++)
101 {
102 p = p->right;
103 }
104 sr = p;
105 s = p->down;
106 while(s!=p && q->j>s->j)
107 {
108 sr = s;
109 s = s->down;
110 }
111 q->down = s;
112 sr->down = q;
113 /**********列链接处理完毕*********************/
114
115 return true;
116 }
117
118 /**********关于矩阵转置的算法,即a[i][j]<->a[j][i]******************/
119 LinkList MatrixTransposition(LinkList head, int m, int n)
120 {
121 LinkList THead = head,p,q,h;
122 int temp;
123 //重新构造十字矩阵,列换行,行换列
124 InitArray(&h,n,m);
125 CreateHead(&h,n,m);
126 for(p = THead->down; p!=THead; p = p->down)
127 {
128
129 for(q = p->right; q!=p; q = q->right)
130 {
131 //j变i,i变j,值不变
132 if(!InsertNode(&h, q->j, q->i, q->value))
133 return NULL;
134 }
135
136 }
137 return h;
138
139 }
140 /*******销毁链表操作******************/
141 void DestroyMatrix(LinkList *head)
142 {
143 LinkList p,q,r;
144 for(p = (*head)->down; p!=*head; p = p->down)
145 {
146
147 for(q = p->right; q!=p;)
148 {
149 r = q->right;
150 free(q);
151 q=r;
152 }
153
154 }
155 }
156 /*************打印矩阵算法*********************/
157 void PrintMatrix(LinkList head,int m,int n)
158 {
159 LinkList p,q;
160
161 cout<<"此矩阵为"<<m<<"*"<<n<<"型"<<endl;
162 //向下推进,按行输出
163 for(p = head->down; p!=head; p = p->down)
164 {
165 cout<<"第"<<p->i<<"行 ";
166 for(q = p->right; q!=p; q = q->right)
167 {
168
169 cout<<" "<<"["<<q->i<<","<<q->j<<"] "<<q->value<<" ";
170 }
171 cout<<endl;
172 }
173 }
174 //以矩阵形式输出
175 void MatrixPrint(LinkList head,int m,int n)
176 {
177 int a[100][100];
178 LinkList p,q;
179 memset(a,0,sizeof(a));//置零
180 for(p = head->down; p!=head; p = p->down)
181 {
182 for(q = p->right; q!=p; q = q->right)
183 {
184 a[q->i][q->j]=q->value;//赋值
185 }
186 }
187 for(int i=0;i<m;i++)
188 {
189 for(int j=0;j<n;j++)
190 {
191 cout<<a[i][j]<<" ";
192 }
193 cout<<endl;
194 }
195 }
196
197 void MainMenu()
198 {
199 LinkList head,h;
200 int m,n,total;//total为矩阵中非零数值个数
201 RECORD RecordMatrix[1000];
202 FILE *fp;
203
204 if((fp = fopen("F:Matrix.txt","r"))==NULL)
205 {
206 cout<<"cannot open the file"<<endl;
207 exit(-1);
208 }
209 //找到矩阵的基本框架
210 fscanf(fp,"%d%d%d",&m,&n,&total);
211 //缓存器record
212 for(int i=0;i<total;i++)
213 {
214 fscanf(fp,"以上是关于数据结构与算法系列研究四——数组和广义表的主要内容,如果未能解决你的问题,请参考以下文章
