数据结构与算法学习笔记 串,数组和广义表
Posted 临风而眠
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构与算法学习笔记 串,数组和广义表相关的知识,希望对你有一定的参考价值。
数据结构与算法学习笔记(6) 串、数组和广义表
截图、笔记来自: 王卓 数据结构与算法
文章目录
一.串
1.串的定义
-
串:零个或多个任意字符组成的有限序列
-

-
几个术语
- 子串:串中任意个连续字符组成的子序列称为该串的子串
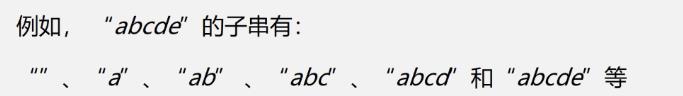
- 真子串是不包含自身的所有子串
- 主串: 包含子串的串相应地称为主串
- 字符位置:字符在序列中的序号为该字符在串中的位置
- 子串位置: 子串第一个字符在主串中的位置
- 空格串:由一个或多个空格组成的串,与空串不同

- 串相等: 当且仅当两个串的长度相等且在各对应位置上字符都相同时,这两个串才相等
- 注意所有空串都相等
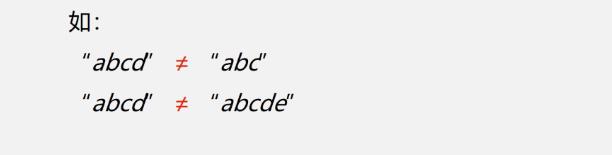
- 子串:串中任意个连续字符组成的子序列称为该串的子串
2.串的类型定义、存储结构及其运算
串的类型定义
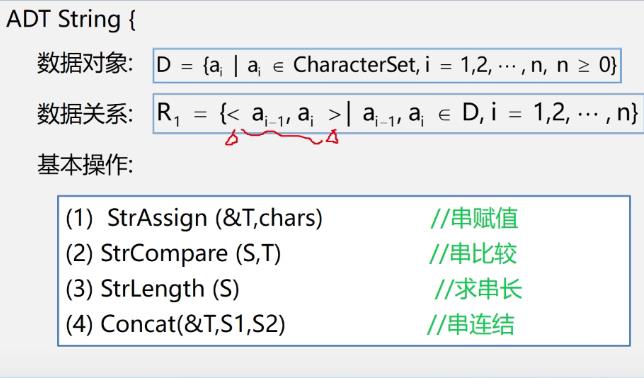

串的存储
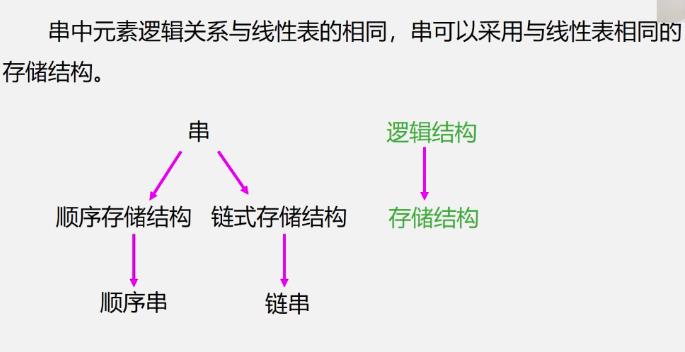
串的顺序存储结构
#define MAXLEN 255
typedef struct{
char ch[MAXLEN+1]; //存储串的一维数组
// 0号单元存放串的长度
int length; //串的当前长度
}SString;
串的链式存储结构

根据需要选择单链表/双向链表/循环链表等
-
优点:操作方便
-
缺点:存储密度低
-

-
解决办法
将多个字符放在一个结点中,以克服其缺点

块链结构
上述解决办法就是块链结构
#define CHUNKSIZE 80 //块的大小可自定义
typedef struct Chunk{
char ch[CHUNKSIZE];
struct Chunk *next;
}Chunk;
typedef struct{
Chunk *head,*tail; //串的头尾指针
int curlen; //串的当前长度
}LString; //字符串的块链结构
顺序存储结构用的更多,因为匹配查找运算用的多,删除插入用的少
3.串的模式匹配算法
-
算法目的:
确定主串中所含子串(模式串)第一次出现的位置(定位)
-
算法应用
搜索引擎、拼写检查、语言翻译、数据压缩
-
算法种类
- BF算法(Brute-force,古典的、经典的、朴素的、穷举的)
- KMP算法(速度快)
①BF算法
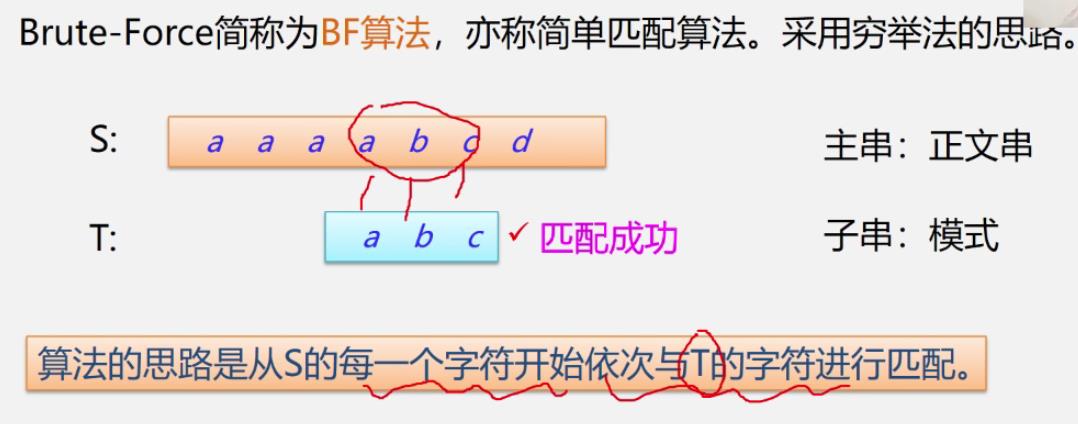
-
例子引入

-
对i-j+2的理解
T从1位置移动到j,移动了j-1个长度,则S也移动了j-1
S现在的位置是i,移动的长度也是j-1,用现在的位置i减去移动的长度i-(j-1),再加1就是下一个位置,所以是i-j+2
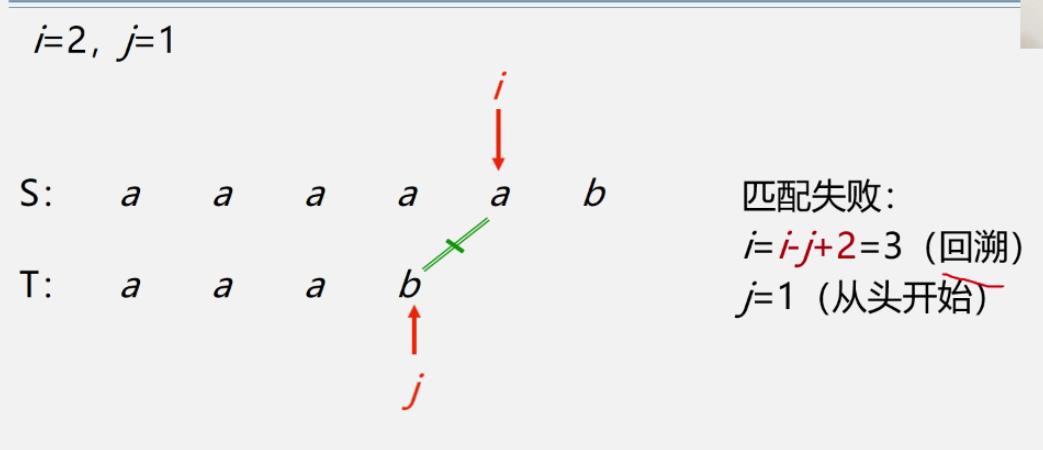

-
-
算法思想

-
算法描述
int Index_BF(SString S,SString T){ int i=1,j=1; while(i<=S.length && j<=T.length){ //j>T.length时说明j的每个字符都匹配成功了,就不用继续匹配了 if(S.ch[i]==t.ch[j]) { ++i; ++j; //主串和子串依次匹配下一个字符 } else { i=i-j+2; j=1; //主串、子串指针回溯重新开始下一次匹配 } } if(j>T.length) return i-T.length; //返回匹配的第一个字符的下标 else return 0; //模式匹配不成功 }or
int Index(SString S, SString T, int pos) { i = pos; j = 1; while (i <= S[0] && j <= T[0]) { if (S[i] == T[j]) { ++i; ++j; } // 继续比较后继字符 else { i = i-j+2; j = 1; } // 指针后退重新开始匹配 } if (j > T[0]) return i-T[0]; else return 0; } // Index -
算法时间复杂度分析
-
最坏时间复杂度:
在最坏情况下,每趟不成功的匹配都发生在模式串T的最后一个字符
那么前n-m趟不成功的匹配比较了(n-m)*m次,最后一趟匹配成功比较了m次,则总共匹配了
(n-m)*m+m次

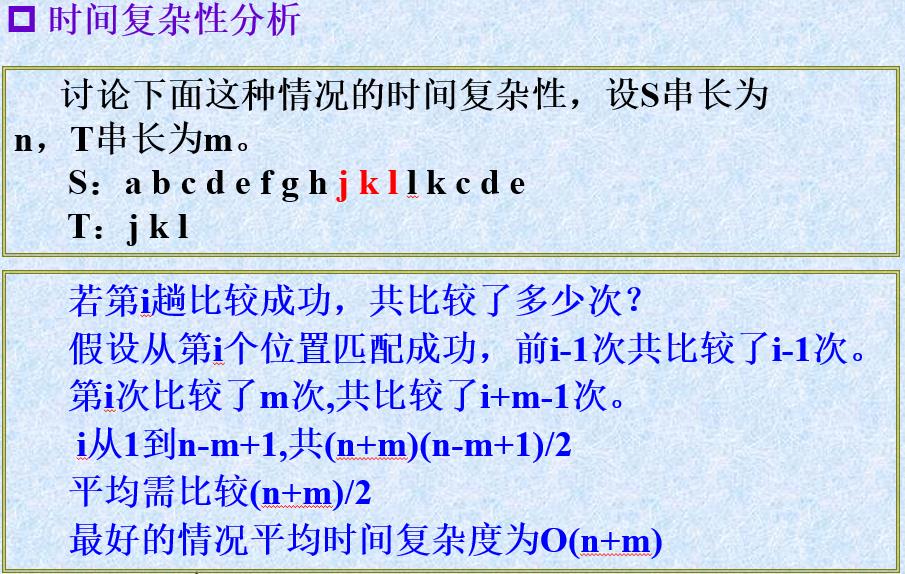

-
②KMP算法
这里听了一遍没理解,去搜了搜别的教程,推荐几个:
👉有个哈工大师兄在B站发的视频讲的挺好


-
小例
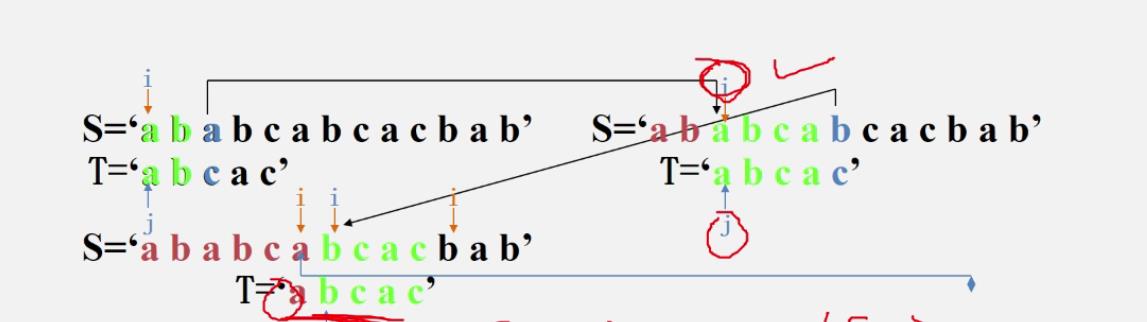
-
算法思想

- 例
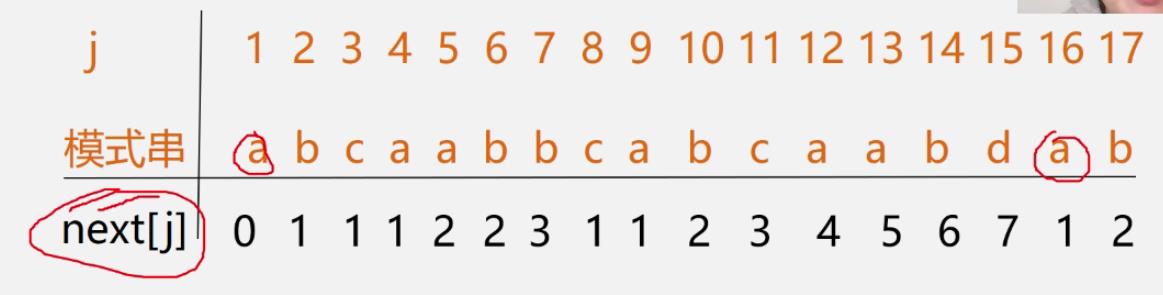
-
算法描述
int index_KMP(SString S,SString T,int pos){ i = pos, j = 1; while(i<S.length && j<T.length){ if(j==0 || S.ch[i]==T.ch[j]){ i++; j++;} else j=next[j]; // i不变,j后退 } if(j>T.length) return i - T.length; //匹配成功 else return 0; //返回不匹配标志 } -
求next数组的函数
void get_next(SString T,int &next[]){ i = 1; next[1]=0; j=0; while(i<T.length){ if(j==0||T.ch[i]==T.ch[j]){ ++i;++j; next[i]=j; } else j = next[j]; } }
二.数组
1.数组的定义及特点
-
数组:按一定格式排列起来的具有相同类型的数据元素的集合
-
一维数组:线性表中的数据元素为非结构的简单元素,则称为一维数组
- 一维数组的逻辑结构:线性结构
- 是定长的线性表
- 声明格式
数据类型 变量名称[长度]; - 一维数组的逻辑结构:线性结构
-
二维数组


二维数组既可以看成线性结构,也可以看成非线性结构
-
声明格式
数据类型 变量名称[行数][列数]; -

array1是有n个元素的一维数组
-
-
三维数组

-
数组特点:结构固定
定义后,维数和维界不再改变
-
数组基本操作

插入删除等操作会破坏数组结构
2.数组的抽象数据类型定义
-
n维数组的抽象数据类型

n n n为数组的维数, b i b_i bi为数组第i维的长度, j i j_i ji为数组元素第i维的下标

3.数组的顺序存储结构

-
一维数组
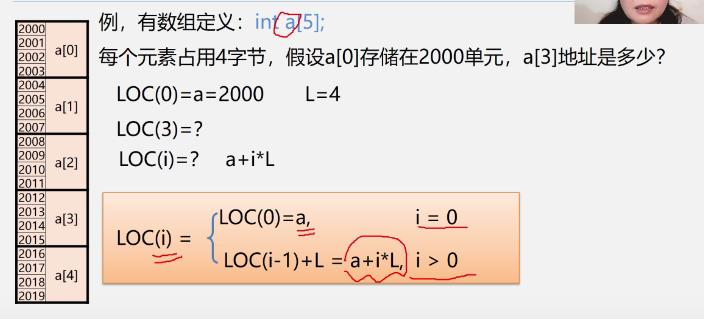
-
二维数组
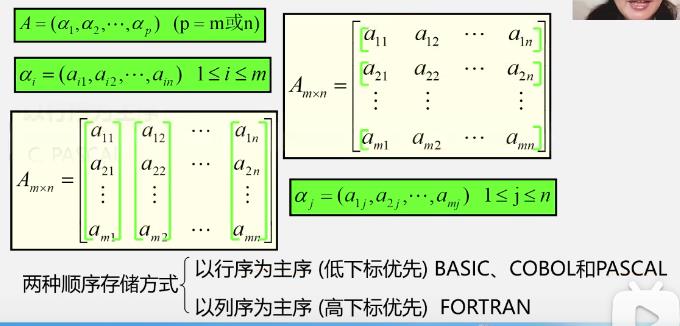

-
以行序为主序
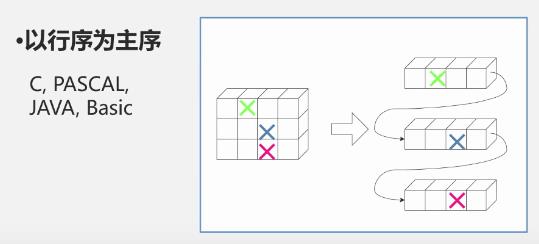
-
以列序为主序
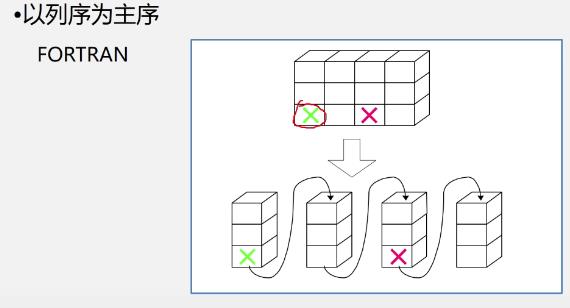

-
二维数组的行序优先表示

-
-
-
三维数组
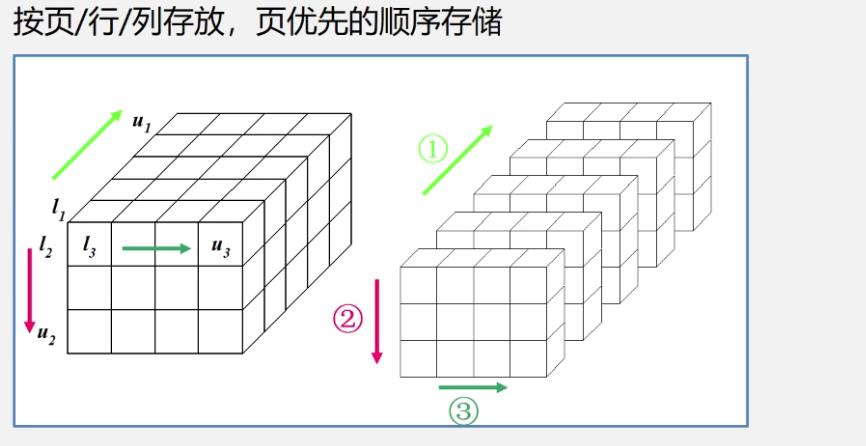

-
n维数组

-
例

4.特殊矩阵的压缩存储


①对称矩阵的压缩存储

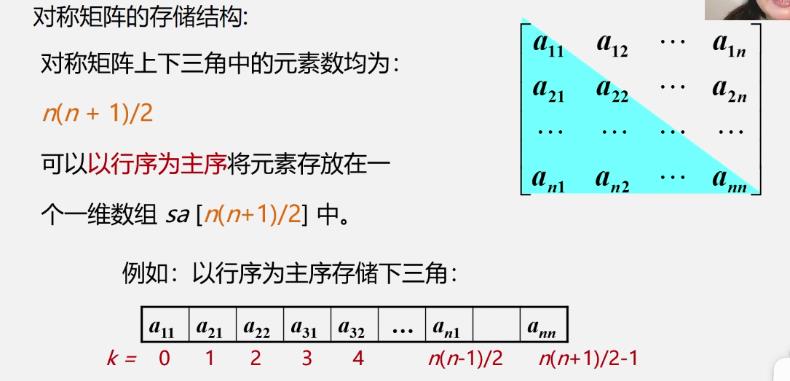
②三角矩阵、对角矩阵的压缩存储
- 三角矩阵

空间里面那个+1是用来存储常数c
- 对角矩阵

③稀疏矩阵的压缩存储
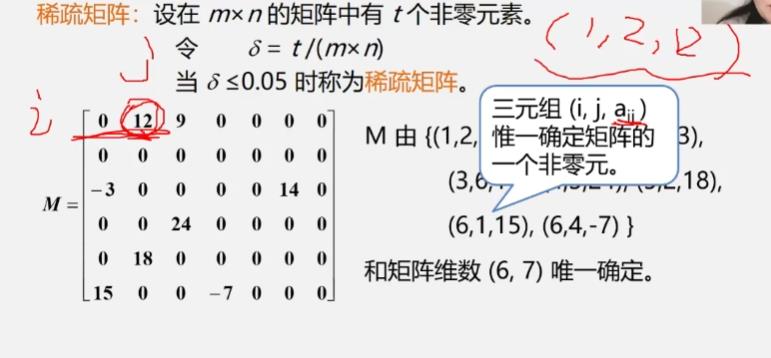
-
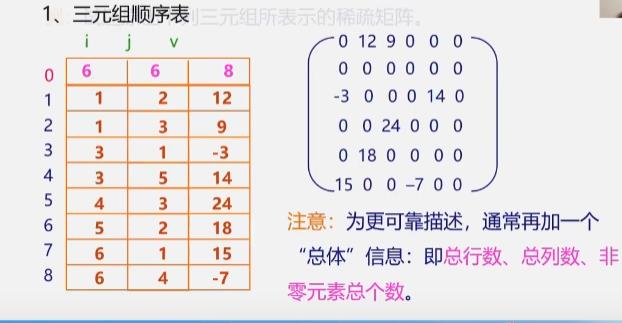
压缩存储原则: 存各非零元的值、行列位置和矩阵的行列数
- 三元组的不同表示方法可决定稀疏矩阵不同的压缩存储方法
三元组顺序表

-
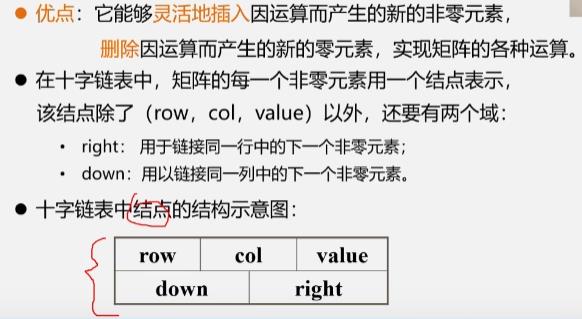
优缺点

下面的十字链表可以克服三元组顺序表的缺点
稀疏矩阵的链式存储结构:十字链表

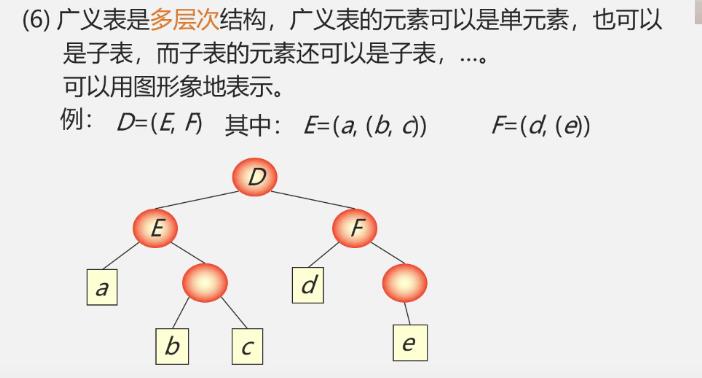
三.广义表
广义表也是递归定义

线性表中的元素是同类型的单一元素
上面说的原子就是指单一元素
-
广义表的一些基本概念


-
广义表的性质

-
广义表和线性表的区别

-
广义表的基本运算

以上是关于数据结构与算法学习笔记 串,数组和广义表的主要内容,如果未能解决你的问题,请参考以下文章

