概率矩阵分解的损失函数为多少比较正常

Posted 2023-04-25

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了概率矩阵分解的损失函数为多少比较正常相关的知识，希望对你有一定的参考价值。

参考技术A 概率矩阵分解的损失函数一般为交叉熵损失、平方损失和KL散度损失，其中KL散度损失是最小化KL散度作为优化目标，因此效果最好，而交叉熵损失和平方损失之间的差异不大，但是从计算效率上来说，交叉熵损失有优势。

基于矩阵分解的协同过滤算法

基于矩阵分解的CF算法实现（一）：LFM

LFM也就是前面提到的Funk SVD矩阵分解

LFM原理解析

LFM(latent factor model)隐语义模型核心思想是通过隐含特征联系用户和物品，如下图：

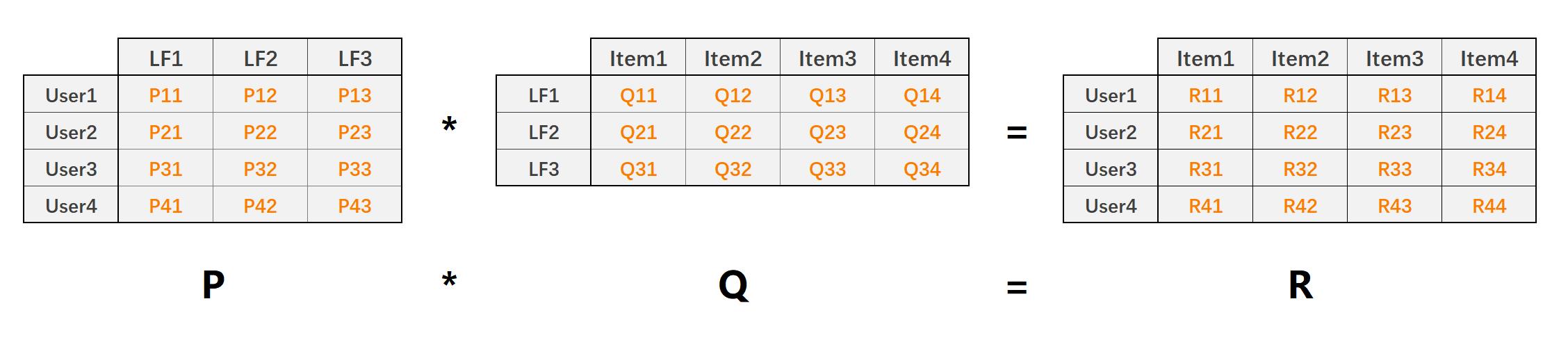
P矩阵是User-LF矩阵，即用户和隐含特征矩阵。LF有三个，表示共总有三个隐含特征。
Q矩阵是LF-Item矩阵，即隐含特征和物品的矩阵
R矩阵是User-Item矩阵，有P*Q得来
能处理稀疏评分矩阵

利用矩阵分解技术，将原始User-Item的评分矩阵（稠密/稀疏）分解为P和Q矩阵，然后利用 $P * Q$ 还原出User-Item评分矩阵 $R$ 。整个过程相当于降维处理，其中：

矩阵值 $P_{11}$ 表示用户1对隐含特征1的权重值
矩阵值 $Q_{11}$ 表示隐含特征1在物品1上的权重值
矩阵值 $R_{11}$ 就表示预测的用户1对物品1的评分，且 $R_{11}=\\vec{P_{1,k}}\\cdot \\vec{Q_{k,1}}$

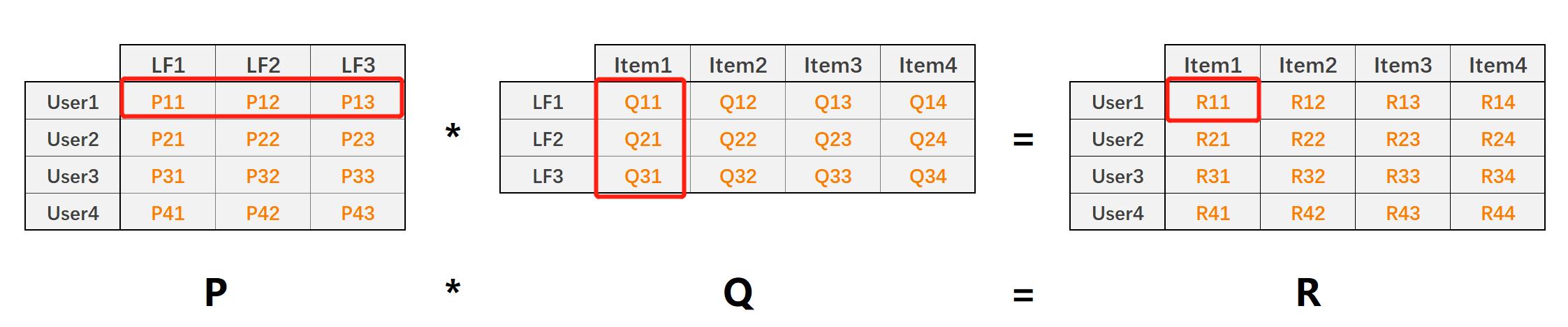
利用LFM预测用户对物品的评分， $k$ 表示隐含特征数量：

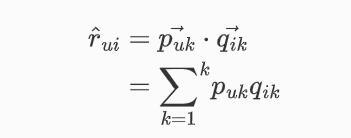
因此最终，我们的目标也就是要求出P矩阵和Q矩阵及其当中的每一个值，然后再对用户-物品的评分进行预测。

损失函数

同样对于评分预测我们利用平方差来构建损失函数：

加入L2正则化：
$\\sum_{u,i\\in R} (r_{ui}-{\\sum_{k=1}}^k p_{uk}q_{ik})^2 + \\lambda(\\sum_U{p_{uk}}^2+\\sum_I{q_{ik}}^2)$
对损失函数求偏导：

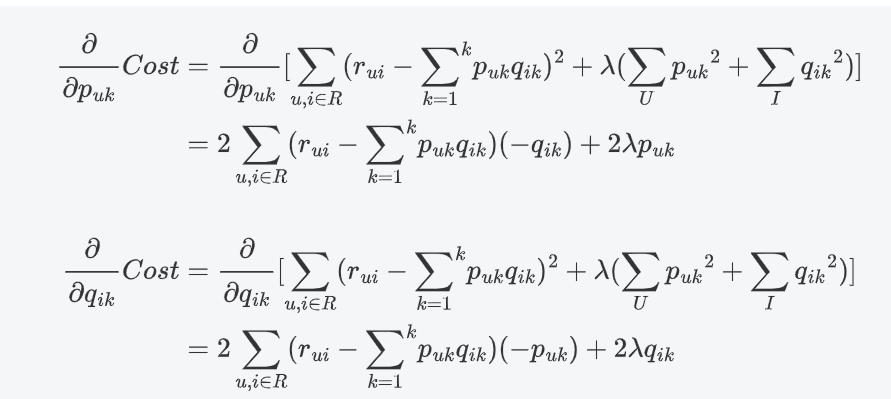
随机梯度下降法优化

梯度下降更新参数 $p_{uk}$ ：

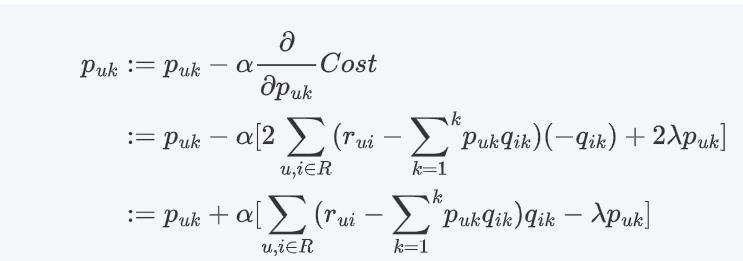
同理：

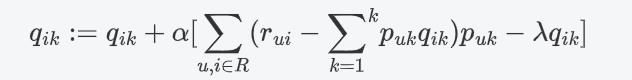
随机梯度下降： 向量乘法每一个分量相乘求和

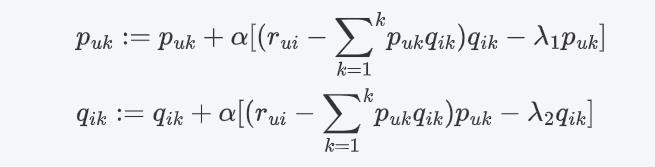
由于P矩阵和Q矩阵是两个不同的矩阵，通常分别采取不同的正则参数，如 $\\lambda_1$ 和 $\\lambda_2$

算法实现

'''
LFM Model
'''
import pandas as pd
import numpy as np

# 评分预测    1-5
class LFM(object):

    def __init__(self, alpha, reg_p, reg_q, number_LatentFactors=10, number_epochs=10, columns=["uid", "iid", "rating"]):
        self.alpha = alpha # 学习率
        self.reg_p = reg_p    # P矩阵正则
        self.reg_q = reg_q    # Q矩阵正则
        self.number_LatentFactors = number_LatentFactors  # 隐式类别数量
        self.number_epochs = number_epochs    # 最大迭代次数
        self.columns = columns

    def fit(self, dataset):
        '''
        fit dataset
        :param dataset: uid, iid, rating
        :return:
        '''

        self.dataset = pd.DataFrame(dataset)

        self.users_ratings = dataset.groupby(self.columns[0]).agg([list])[[self.columns[1], self.columns[2]]]
        self.items_ratings = dataset.groupby(self.columns[1]).agg([list])[[self.columns[0], self.columns[2]]]

        self.globalMean = self.dataset[self.columns[2]].mean()

        self.P, self.Q = self.sgd()

    def _init_matrix(self):
        '''
        初始化P和Q矩阵，同时为设置0，1之间的随机值作为初始值
        :return:
        '''
        # User-LF
        P = dict(zip(
            self.users_ratings.index,
            np.random.rand(len(self.users_ratings), self.number_LatentFactors).astype(np.float32)
        ))
        # Item-LF
        Q = dict(zip(
            self.items_ratings.index,
            np.random.rand(len(self.items_ratings), self.number_LatentFactors).astype(np.float32)
        ))
        return P, Q

    def sgd(self):
        '''
        使用随机梯度下降，优化结果
        :return:
        '''
        P, Q = self._init_matrix()

        for i in range(self.number_epochs):
            print("iter%d"%i)
            error_list = []
            for uid, iid, r_ui in self.dataset.itertuples(index=False):
                # User-LF P
                ## Item-LF Q
                v_pu = P[uid] #用户向量
                v_qi = Q[iid] #物品向量
                err = np.float32(r_ui - np.dot(v_pu, v_qi))

                v_pu += self.alpha * (err * v_qi - self.reg_p * v_pu)
                v_qi += self.alpha * (err * v_pu - self.reg_q * v_qi)
                
                P[uid] = v_pu 
                Q[iid] = v_qi

                # for k in range(self.number_of_LatentFactors):
                #     v_pu[k] += self.alpha*(err*v_qi[k] - self.reg_p*v_pu[k])
                #     v_qi[k] += self.alpha*(err*v_pu[k] - self.reg_q*v_qi[k])

                error_list.append(err ** 2)
            print(np.sqrt(np.mean(error_list)))
        return P, Q

    def predict(self, uid, iid):
        # 如果uid或iid不在，我们使用全剧平均分作为预测结果返回
        if uid not in self.users_ratings.index or iid not in self.items_ratings.index:
            return self.globalMean

        p_u = self.P[uid]
        q_i = self.Q[iid]

        return np.dot(p_u, q_i)

    def test(self,testset):
        '''预测测试集数据'''
        for uid, iid, real_rating in testset.itertuples(index=False):
            try:
                pred_rating = self.predict(uid, iid)
            except Exception as e:
                print(e)
            else:
                yield uid, iid, real_rating, pred_rating

if __name__ == '__main__':
    dtype = [("userId", np.int32), ("movieId", np.int32), ("rating", np.float32)]
    dataset = pd.read_csv("datasets/ml-latest-small/ratings.csv", usecols=range(3), dtype=dict(dtype))

    lfm = LFM(0.02, 0.01, 0.01, 10, 100, ["userId", "movieId", "rating"])
    lfm.fit(dataset)

    while True:
        uid = input("uid: ")
        iid = input("iid: ")
        print(lfm.predict(int(uid), int(iid)))

基于矩阵分解的CF算法实现（二）：BiasSvd

BiasSvd其实就是前面提到的Funk SVD矩阵分解基础上加上了偏置项。

BiasSvd

利用BiasSvd预测用户对物品的评分， $k$ 表示隐含特征数量：

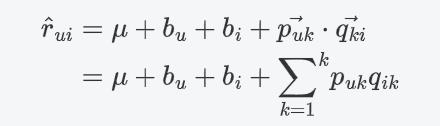
损失函数

同样对于评分预测我们利用平方差来构建损失函数：

加入L2正则化：
$\\sum_{u,i\\in R} (r_{ui}-\\mu - b_u - b_i-{\\sum_{k=1}}^k p_{uk}q_{ik})^2 + \\lambda(\\sum_U{b_u}^2+\\sum_I{b_i}^2+\\sum_U{p_{uk}}^2+\\sum_I{q_{ik}}^2)$