损失函数的概率验证及性质

Posted 2020-10-09 迈克老狼2012

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了损失函数的概率验证及性质相关的知识，希望对你有一定的参考价值。

从http://www.cnblogs.com/mikewolf2002/p/7560748.html这篇文章中，我们知道损失函数为下面的形式：

\\[J(\\theta_0, \\theta_1..., \\theta_n) = \\frac{1}{2m}\\sum\\limits_{i=0}^{m}(h_\\theta(x_0^{(i)}, x_1^{(i)}, ...,x_n^{(i)})- y^{(i)})^2\\]

或者

\\[J(\\mathbf\\theta) = \\frac{1}{2}(\\mathbf{X\\theta} - \\mathbf{Y})^T(\\mathbf{X\\theta} - \\mathbf{Y})\\]

为什么选这个函数为损失函数呢？也就是说为什么选择最小二乘作为指标来计算回归方程参数？这个可以用概率论的方法进行证明。

首先我们提供一组假设，依据这些假设，来证明选择最小二乘是合理的。

（1）假设1：

假设输入与输出为线性函数关系，表示为：\\(y^{(i)}=\\theta^Tx^{(i)}+\\epsilon^{(i)}\\)

其中\\(\\epsilon^{(i)}\\)为误差项，这个参数可以理解为对未建模效应的捕获，如果还有其他特征，这个误差项表示了一种我们没有捕获的特征，或者看成一种随机的噪声。

假设\\(\\epsilon^{(i)}\\)服从高斯分布（正态分布）\\(\\epsilon^{(i)} \\sim N(0,\\sigma^2)\\)，表示一个均值是0，方差是\\(\\sigma^2\\)的高斯分布,且每个误差项彼此之间是独立的，并且他们服从均值和方差相同的高斯分布(IID independently and identically distributed,独立同分布)。

那么高斯分布的概率密度函数：

\\[p(\\epsilon^{(i)})=\\frac{1}{\\sqrt{2\\pi}\\sigma}exp\\big(-\\frac{(\\epsilon^{(i)})^2}{2\\sigma^2}\\big)\\]

根据上述两式可得：

\\[p(y^{(i)}|x^{(i)};\\theta)=\\frac{1}{\\sqrt{2\\pi}\\sigma}exp\\big(-\\frac{(y^{(i)}-\\theta^Tx^{(i)})^2}{2\\sigma^2}\\big)\\]

注意： \\(\\theta\\)并不是一个随机变量，而是一个尝试估计的值，就是说它本身是一个常量，只不过我们不知道它的值，所以上式中用分号表示。分号应读作“以…作为参数”，上式读作“给定\\(x^{(i)}\\)以\\(\\theta\\)为参数的\\(y^{(i)}\\)的概率服从高斯分布”。

即在给定了特征与参数之后，输出是一个服从高斯分布的随机变量,可描述为：\\(y^{(i)}|x^{(i)};\\theta \\sim N(\\theta^Tx^{(i)},\\sigma^2)\\)，

为什么选取高斯分布？

1) 便于数学处理。

2) 对绝大多数问题，如果使用了线性回归模型，然后测量误差分布，通常会发现误差是高斯分布的。

3) 中心极限定律：若干独立的随机变量之和趋向于服从高斯分布。若误差有多个因素导致，这些因素造成的效应的总和接近服从高斯分布。

（2）假设2：

给定\\(X\\)（特征矩阵，包含所有的\\(x^{(i)}\\))和\\(\\theta\\),如何描述\\(y^{(i)}\\)的概率呢？首先我们可以把\\(y^{(i)}\\)的概率写成\\(p(\\overrightarrow{y}|X;\\theta)\\)。这个概率可以把\\(\\theta\\)看成为固定值，\\(\\overrightarrow{y}\\)或\\(X\\)的函数。我们称这个函数为\\(\\theta\\)的似然函数。

\\[L(\\theta)=L(\\theta;X,\\overrightarrow{y})=p(\\overrightarrow{y}|X;\\theta)\\]

由于\\(\\epsilon^{(i)}\\)是独立同分布，所以给定\\(x^{(i)}\\)情况下\\(y^{(i)}\\)也是独立同分布，则上式可写成所有分布的乘积：

\\[\\begin{align*} L(\\theta) &=\\prod_{i=1}^{m}p(y^{(i)}|x^{(i)};\\theta) \\\\
&=\\prod_{i=1}^{m}\\frac{1}{\\sqrt{2\\pi}\\sigma}exp\\big(-\\frac{(y^{(i)}-\\theta^Tx^{(i)})^2}{2\\sigma^2}\\big) \\end{align*}\\]

（3）假设3：

极大似然估计：选取\\(\\theta\\)使似然性\\(L(\\theta)\\)最大化（数据出现的可能性尽可能大）

定义\\(L(\\theta)\\)对数似然函数为：

\\begin{align*}l(\\theta) &= logL(\\theta) \\\\ &=log\\prod_{i=1}^{m}\\frac{1}{\\sqrt{2\\pi}\\sigma}exp\\big(-\\frac{(y^{(i)}-\\theta^Tx^{(i)})^2}{2\\sigma^2}\\big) \\\\ &=\\sum\\limits_{i=1}^{m}log\\frac{1}{\\sqrt{2\\pi}\\sigma}exp\\big(-\\frac{(y^{(i)}-\\theta^Tx^{(i)})^2}{2\\sigma^2}\\big) \\\\ &=mlog\\frac{1}{\\sqrt{2\\pi}\\sigma}-\\frac{1}{\\sigma^2}*\\frac{1}{2}\\sum\\limits_{i=1}^m(y^{(i)}-\\theta^Tx^{(i)})^2\\end{align*}

上式两个加项，前一项为常数。所以，使似然函数最大，就是使后一项最小，即：\\(\\frac{1}{2}\\sum\\limits_{i=1}^m(y^{(i)}-\\theta^Tx^{(i)})^2\\)

这一项就是之前的\\(J(\\theta)\\)，由此得证，之前的最小二乘法计算参数，实际上是假设了误差项满足高斯分布，且独立同分布的情况，使\\(\\theta\\)似然最大化来计算参数。

注意：高斯分布的方差对最终结果没有影响，由于方差一定为正数，所以无论取什么值，最后结果都相同。

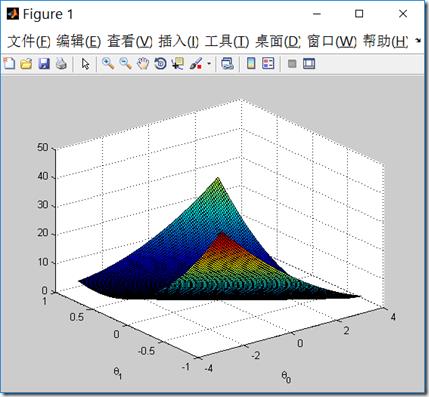
假设\\(h_{\\theta}(x)=\\theta_{0}+\\theta_{1}x\\),下面在matlib中画出损失函数\\(J(\\theta)\\)。

样本文件下载：ex2Data.zip

代码如下：

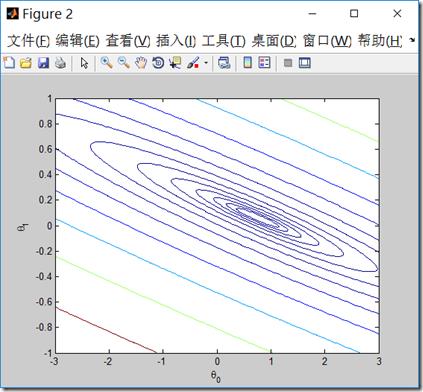
clear all; close all; clc;
J_vals = zeros(100, 100);   % 初始化损失函数参数矩阵，假设只有theta_0, theta_1
theta0_vals = linspace(-3, 3, 100); %范围-3,3,100个值
theta1_vals = linspace(-1, 1, 100); %范围-1,1,100个值
x = load(\'ex2x.dat\');
y = load(\'ex2y.dat\');
m = length(x);
x = [ones(m, 1) x];
%循环theta0,theta1
for i = 1:length(theta0_vals)
	  for j = 1:length(theta1_vals)
	      t = [theta0_vals(i); theta1_vals(j)];
	      J_vals(i,j) = 0;
          for k = 1:m
             J_vals(i,j) = J_vals(i,j)+(x(k,:)*t-y(k))^2;
          end
          J_vals(i,j) = J_vals(i,j)/(2*m);
    end
end

% 用surf函数来画损失函数
J_vals = J_vals\'
figure;
surf(theta0_vals, theta1_vals, J_vals)
xlabel(\'\\theta_0\'); ylabel(\'\\theta_1\')
figure;
% 画损失函数的轮廓，注意范围是0.01 - 100,总共15个轮廓
contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 2, 15))
xlabel(\'\\theta_0\'); ylabel(\'\\theta_1\')