哈密尔顿环 dfs
Posted 橘生淮南终洛枳
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了哈密尔顿环 dfs相关的知识，希望对你有一定的参考价值。
1.哈密尔顿环
( ⊙ o ⊙ ) 题目：
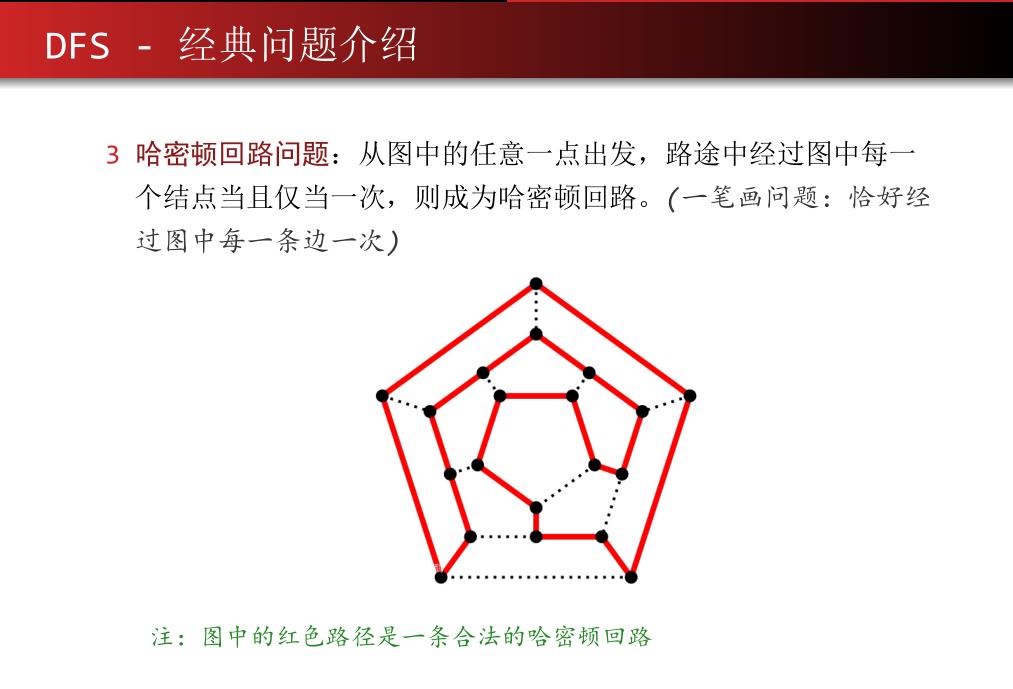
(⊙v⊙)嗯，代码：
#include <cstdio> #include <algorithm> using namespace std; const int N = 25; int n, cnt; int a[N][N]; int v[N], p[N]; void print() { printf("Route #%d: ", ++cnt);//路径条数 for(int i=1; i<=p[0]; i++) printf("%d - ", p[i]); printf("1\\n"); } void dfs(int x) { v[x] = 1, p[++p[0]] = x; if(p[0] == n) { if(a[p[0]][1]) print(); } else for(int i=1; i<=n; i++) if(a[x][i] && !v[i]) dfs(i); v[x] = 0, p[p[0]] = 0, --p[0];//回溯过程 } int main() { scanf("%d", &n); for(int i=1; i<=n; i++) for(int j=1; j<=n; j++) scanf("%d", &a[i][j]);//输入一个表示i，j之间是否有边的矩阵 dfs(1); return 0; }
2.数独
@_@ 题目：
思路 就是纯粹的dfs，类似于八皇后的问题
#include<iostream> #include<cstdio> using namespace std; const int N = 9; const int Group[9][9] = { 0, 0, 0, 1, 1, 1, 2, 2, 2, 0, 0, 0, 1, 1, 1, 2, 2, 2, 0, 0, 0, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5, 3, 3, 3, 4, 4, 4, 5, 5, 5, 3, 3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 6, 7, 7, 7, 8, 8, 8, 6, 6, 6, 7, 7, 7, 8, 8, 8, 6, 6, 6, 7, 7, 7, 8, 8, 8 }; int a[N][N],Line[N][N],Column[N][N],group[N][N]; int print() { for(int i=0; i<N; i++) { for(int j=0; j<N; j++) cout<<a[i][j]+1<<" "; cout<<endl; } } void dfs(int x,int y) { if(x == N) { print(); return ; } int nxt_x = x,nxt_y = y + 1; if(nxt_y == N) nxt_x = x + 1,nxt_y = 0; if(a[x][y] >= 0) dfs(nxt_x,nxt_y); else { for(int i=0; i<N; i++) { if(!Line[x][i] && !Column[y][i] && !group[Group[x][y]][i]) { Line[x][i] = Column[y][i] = group[Group[x][y]][i] = 1; a[x][y] = i; dfs(nxt_x,nxt_y); a[x][y] = -1; Line[x][i] = Column[y][i] = group[Group[x][y]][i] = 0; } } } } int main() { for(int i=0; i<N; i++) for(int j=0; j<N; j++) cin>>a[i][j], a[i][j]--; for(int i=0; i<N; i++) for(int j=0; j<N; j++) if(a[i][j] >= 0) { Line[i][a[i][j]] = 1, Column[j][a[i][j]] = 1, group[Group[i][j]][a[i][j]] = 1; } dfs(0,0); return 0; }
3.倒水问题： Pots
| Time Limit: 1000MS | Memory Limit: 65536K | |||
| Total Submissions: 19116 | Accepted: 8074 | Special Judge | ||
Description
You are given two pots, having the volume of A and B liters respectively. The following operations can be performed:
- FILL(i) fill the pot i (1 ≤ i ≤ 2) from the tap;
- DROP(i) empty the pot i to the drain;
- POUR(i,j) pour from pot i to pot j; after this operation either the pot j is full (and there may be some water left in the pot i), or the pot i is empty (and all its contents have been moved to the pot j).
Write a program to find the shortest possible sequence of these operations that will yield exactly C liters of water in one of the pots.
Input
On the first and only line are the numbers A, B, and C. These are all integers in the range from 1 to 100 and C≤max(A,B).
Output
The first line of the output must contain the length of the sequence of operations K. The following K lines must each describe one operation. If there are several sequences of minimal length, output any one of them. If the desired result can’t be achieved, the first and only line of the file must contain the word ‘impossible’.
Sample Input
3 5 4
Sample Output
6 FILL(2) POUR(2,1) DROP(1) POUR(2,1) FILL(2) POUR(2,1)
Source
Northeastern Europe 2002, Western Subregion
思路：
此题分为6种情况，分别为第一个倒空，第二个倒空，第一个倒满，第二个倒满，第一个给第二个，第二个给第一个，那么就依次判断这几种情况，注意判重情况就行。具体细节全在代码里，直接看代码！！
(⊙v⊙)嗯~ 代码：
#include<cstdio> #include<queue> #include<cstdlib> #include<cstring> using namespace std; int a,b,z,xu; bool v[1000000]; int solution[1000000],cnt,pre[1000000]; struct node { int x,y,s,id; } cur,nxt; queue<node>p; void output(int w) { if(!w) return; else output(pre[w]); switch(solution[w]) { case 1: printf("FILL(1)\\n"); break; case 2: printf("FILL(2)\\n"); break; case 3: printf("DROP(1)\\n"); break; case 4: printf("DROP(2)\\n"); break; case 5: printf("POUR(2,1)\\n"); break; case 6: printf("POUR(1,2)\\n"); } } void pan(int i,int j,int w) { if(i==z||j==z) { printf("%d\\n",nxt.s); output(w); exit(0); } } int main() { while(scanf("%d%d%d",&a,&b,&z)==3) {//多组数据输入 if(a==z) {//如果A杯、B杯直接是满的，直接输出就行了 printf("1\\n"); printf("FILL(1)\\n"); return 0; } else if(b==z) { printf("1\\n"); printf("FILL(2)\\n"); return 0; } while(!p.empty()) p.pop(); cnt=0;//多组数据输入要初始化 memset(v,0,sizeof(v)); memset(solution,0,sizeof(solution)); //bfs 基本流程让初始元素入队 //代码展示的是让一空一满入队的情况（所以入队两个），还有就是让两个空杯子入队的情况（同时入队） cur.x=a; cur.y=0; cur.s=1; cur.id=++cnt; solution[cnt]=1; p.push(cur); cur.x=0; cur.y=b; cur.s=1; cur.id=++cnt; solution[cnt]=2; p.push(cur); while(!p.empty()) { cur=p.front();//取队头元素 if(!cur.x) { //A杯子为空 //当A杯子为空时就只能对它进行一种操作，就是将它填满，B杯子不变，步数+1 nxt.x=a; nxt.y=cur.y; nxt.s=cur.s+1; nxt.id=++cnt; pre[cnt]=cur.id; solution[cnt]=1;//id记录位于队列中的什么位置 pan(nxt.x,nxt.y,cnt);//判断元素是否为最后的元素 //可以开一个二维数组来判断，（更好理解），代码展示的是*1000 //因为数据范围是100的，所以*1000后补三个0，保证了如果输入的不同那么，这个数不会相同 if(!v[nxt.x*1000+nxt.y]) { //判重 v[nxt.x*1000+nxt.y]=true; p.push(nxt); } } if(!cur.y) { //第二个杯子为空 //同上 nxt.x=cur.x; nxt.y=b; nxt.s=cur.s+1; nxt.id=++cnt; pre[cnt]=cur.id; solution[cnt]=2; pan(nxt.x,nxt.y,cnt); if(!v[nxt.x*1000+nxt.y]) { v[nxt.x*1000+nxt.y]=true; p.push(nxt); } } if(cur.x) { //当A不为空时 nxt.x=0; nxt.y=cur.y; nxt.s=cur.s+1; nxt.id=++cnt; pre[cnt]=cur.id; solution[cnt]=3; if(!v[nxt.x*1000+nxt.y]) { v[nxt.x*1000+nxt.y]=true; p.push(nxt); } } if(cur.y) { nxt.x=cur.x; nxt.y=0; nxt.s=cur.s+1; nxt.id=++cnt; pre[cnt]=cur.id; solution[cnt]=4; if(!v[nxt.x*1000+nxt.y]) { v[nxt.x*1000+nxt.y]=true; p.push(nxt); } } if(cur.x||cur.y) { //两个杯子互倒 //B往A中倒 xu=a-cur.x;//计算出倒满A杯子需要的水的体积 if(cur.y>xu) {//如果B杯中水的体积比需要的水的体积大 nxt.x=a; nxt.y=cur.y-xu; } //A杯满了，B杯还有剩余 else {//如果B杯中水的体积比需要的水的体积小 nxt.x=cur.x+cur.y; nxt.y=0; }//A杯等于两者之和，B杯空了 nxt.s=cur.s+1;//步数+1 nxt.id=++cnt; pre[cnt]=cur.id; solution[cnt]=5; pan(nxt.x,nxt.y,cnt); if(!v[nxt.x*1000+nxt.y]) { v[nxt.x*1000+nxt.y]=true; p.push(nxt); } //A往B中倒 xu=b-cur.y;//同上 if(cur.x>xu) { nxt.y=b; nxt.x=cur.x-xu; } else { nxt.y=cur.x+cur.y; nxt.x=0; } nxt.s=cur.s+1; nxt.id=++cnt; pre[cnt]=cur.id; solution[cnt]=6; pan(nxt.x,nxt.y,cnt); if(!v[nxt.x*1000+nxt.y]) { v[nxt.x*1000+nxt.y]=true; p.push(nxt); } } p.pop();//执行完任一操作后出队 } printf("impossible\\n"); } }
自己选的路，跪着也要走完！！！
以上是关于哈密尔顿环 dfs的主要内容，如果未能解决你的问题，请参考以下文章