动态规划初探 -- 背包问题

Posted 2020-06-08

在为期一个星期的ACM集训之后，我就这样做了一个逃兵hhhh

在这一个星期里面，学长讲了快速排序，二分三分搜索，矩阵快速幂，线段树，BFS（广度优先搜索）和DFS（深度优先搜索），邻接表和哈希表，结构体和优先队列，背包问题和动态规划。

其中讲快速排序那天我还在考试，就没有去听，第二天找学长的时候也听得似懂非懂。

学长讲矩阵快速幂的时候爸妈来找我，也没有听。其中基本都学的不扎实。

所以都要后期重新再学一遍，巩固扎实。估计学长还会讲并查集和最小生成树，我就自己看看书吧~

 

=========================================

以上就是背景，下面今天我重新看了看动态规划。动态规划的入门基本逃不出 01背包问题。

可能这是一个基本的必经问题：

有一个包和n个物品，包的容量为m，每个物品都有各自的体积和价值，问当从这n个物品中选择多个物品放在包里而物品体积总数不超过包的容量m时，能够得到的最大价值是多少？

这个问题，学长当时给了几个例子：有三个背包，分别重3，3，5.他们的价值分别是6，6，9.背包的最大的载重量为10.问该怎么选择背包。

我因为比较贪婪，肯定选择价值大的，先选择9。其实这就体现了贪心算法，先只顾眼前的利益。

但是学长说，有些人会先看价值利益的量，比如前两个的背包的价值量是2，第三个背包的价值量是9/5。明显人们应该喜欢小而精美的物品，应该选择前两个的才能更能拿到有价值的东西。

我顿时想想觉得非常有道理。但是如果你仔细想想，如果我选择了前两个，他们的总价值为12，但是他们的总质量是6，不能把第三个物品再装到包里，这就造成了包的浪费。

而如果我选择重量分别为3，5的物品，我的价值总共能够拿到6+9= 15 的物品！

所以我们在选物品的时候要多次比较，一直选一种方案比较到底，然后再进行下一条方案，这里就要用到DFS。

 比如选了物品A，然后选择物品B，或者选择物品C。然后选择物品B的接着选择物品C，而选择物品C的选择物品B。

有点累死二叉树的感觉，但是子节点要比二叉树多。二叉树的基础题可以做一下我们学校的OJ里面的一个基础题：数字三角形 

这道题目我刚开始做得时候其实用了动态规划，但是当时我还是不懂动态规划的思想。

这道题目当时的代码：

#include <stdio.h>

int main(){
    int n=0;
    while(scanf("%d",&n)!=EOF){
        if(n==0){
            break;
        }
        int num[255][255]={};
        int output[255][255]={};
        for(int i=1;i<=n;i++){
            for(int j=1;j<=i;j++){
                scanf("%d",&num[i][j]);
             }
         }
         for(int i=1;i<=n;i++){
            output[n][i]=num[n][i];
          }
          for(int i=n-1;i>=1;i--){
            for(int j=1;j<=i;j++){
                if(output[i+1][j+1]>output[i+1][j]){
                    output[i][j]=output[i+1][j+1]+num[i][j];
                }
                else{
                    output[i][j]=output[i+1][j]+num[i][j];
                }
            }
          }
          printf("%d\n",output[1][1]);
    }
 }

　　这个是练手，其实就是从最上面开始看起，先比较下面两个，选择比较大的那一个。这就用到了贪心算法的思想。

咳咳，好像有点跑题了，继续回到背包问题。

用我们学长的话来概括好了：

当我们在考虑第i个物品的时候，实际上我们只需要关心前i-1个物品能组合出什么样的体积，我们并不关心每一种组合到底是什么样的。 因为组合数量实在太多了，我们需要抓住这些组合的“共性”。从来抽象出可以承受的状态数

 

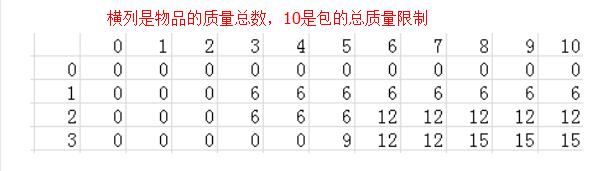
#include <cstdio>
#include <iostream>
#include <cstring>
#include <cmath>
#include <queue>
#include <vector>

using namespace std;

const int N = 100;
int dp[N][N] = {};
int n,m;

struct node{
    int w;
    int v;
    node(int a = 0,int b = 0){
        w = a;
        v = b;
    }
}bags[N];

int main(){
    while(~scanf("%d%d",&n,&m)){
        for(int i = 1;i <= n;i++){
            scanf("%d%d",&bags[i].w,&bags[i].v);
        }
        memset(dp,0,sizeof(dp));
        for(int i = 1;i <= n;i++){
            for(int j = m;j >= 0;j--){
               dp[i][j] = dp[i-1][j];
                if(j >=bags[i].w) dp[i][j] = max(dp[i-1][j],dp[i-1][j-bags[i].w]+bags[i].v);
            }
        }

        for(int i = 1;i <= n;i++){
            for(int j = 0;j <= m;j++){
                printf("%+d ",dp[i][j]);
            }puts("");
        }
        printf("%d",dp[n][m]);
    }    
}

/*
NOTE:
With three bags weight 3,3,5.And the values are 6,6,9
 */

　　昨天在杭电的BestCoder来了一发，只能怪自己基础薄弱，只做出第一题，第二题就因为自己考虑非常多就卡住了，然后在那边写了一个多小时还没有写出来。

但正是因为想得非常多，到hack时间的时候就hack掉了一个人，第一次hack成功哈哈

第一次参加BestCoder名字就这么顺利地变绿了^_^而且接近变蓝。我要继续努力，早日变蓝