数据结构之树

Posted 2020-09-15 Tan

数据结构之树

平均操作时间O(log N).

定义

定义树的一种自然方式是递归方法。
一棵树是一些节点的集合。这个集合可以是空集；若非空，则这一颗树由称做根的节点r以及0个或多个非空的树T1,T2,…..Tk组成，这些子树中每一棵的根都被来自根r的一条有向的边所连接。
一棵树是N个节点和N-1条边的集合，其中的一个节点叫做根。
在一棵树中从根到每个节点恰好存在一条路径。
对任意节点Ni，Ni的深度为从根到Ni的唯一路径的厂。因此，根的深度为0。
Ni的高是从Ni到一片树叶的最长路径的长。因此，所有树叶的高都是0。
一棵树的高等于它根的高。
一棵树的所有节点的深度称为内部路径长

二叉树

二叉树是一颗树，其中每个节点都不能多余二个儿子。
二叉树的一个性质是平均二叉树的深度要比N小得多。

实现

因为一颗二叉树最多可以有两个儿子，所以可以用指针指向它们。

表达式树例子

 

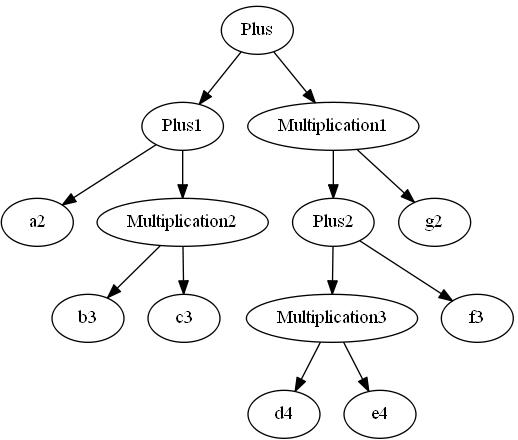
中序遍历：(a+b*c)+((d*e+f)*g)
后序遍历：abc*+de*f+g*+
先序遍历:++a*bc*+*defg

查找树ADT-二叉查找树

  1 #include <stdio.h>
  2 #include <stdlib.h>
  3 #include <vcruntime.h>
  4 
  5 struct TreeNode;
  6 typedef  struct TreeNode *Position;
  7 typedef  struct TreeNode *SearchTree;
  8 
  9 struct TreeNode
 10 {
 11     int Element;
 12     SearchTree Left;
 13     SearchTree Right;
 14 };
 15 
 16 SearchTree CreateTree(SearchTree T) 
 17 {
 18     SearchTree R=malloc(sizeof(struct TreeNode));
 19     T->Element=6;
 20     //T->Left=malloc(sizeof(struct TreeNode));
 21     //T->Right=malloc(sizeof(struct TreeNode));
 22     return T;
 23 }
 24 
 25 //初始化
 26 SearchTree MakeEmpty(SearchTree T)
 27 {
 28     if (T != NULL)
 29     {
 30         MakeEmpty(T->Left);
 31         MakeEmpty(T->Right);
 32         free(T);
 33     }
 34     return NULL;
 35 }
 36 
 37 Position Find(int X, SearchTree T)
 38 {
 39     if (T == NULL)
 40     {
 41         return NULL;
 42     }
 43     if (X < T->Element)
 44     {
 45         return Find(X, T->Left);
 46     }
 47     else if (X > T->Element)
 48     {
 49         return Find(X, T->Right);
 50     }
 51     else
 52     {
 53         return T;
 54     }
 55 }
 56 
 57 //递归
 58 Position FindMin(SearchTree T)
 59 {
 60     if (T == NULL)
 61     {
 62         return NULL;
 63     }
 64     else if (T->Left == NULL)
 65     {
 66         return T;
 67     }
 68     else
 69     {
 70         return FindMin(T->Left);
 71     }
 72 }
 73 
 74 //循环
 75 Position FindMax(SearchTree T)
 76 {
 77     if (T != NULL)
 78     {
 79         while (T->Right != NULL)
 80         {
 81             T = T->Right;
 82         }
 83 
 84     }
 85     return T;
 86 }
 87 
 88 //插入
 89 SearchTree Insert(int X, SearchTree T)
 90 {
 91     if (T == NULL)
 92     {
 93         T = malloc(sizeof(struct TreeNode));
 94         if (T == NULL)
 95         {
 96             printf("Error");
 97         }
 98         else
 99         {
100             T->Element = X;
101             T->Left = T->Right = NULL;
102         }
103     }
104     else
105     {
106         if (X < T->Element)
107         {
108             T->Left = Insert(X, T->Left);
109         }
110         else if (X > T->Element)
111         {
112             T->Right = Insert(X, T->Right);
113         }
114     }
115     return   T;
116 }
117 
118 //删除
119 SearchTree Delete(int X, SearchTree T)
120 {
121     Position TmpCell;
122     if (T == NULL)
123     {
124         printf("Error");
125     }
126     else if (X < T->Element)
127     {
128         T->Left = Delete(X, T->Left);//向左查找
129     }
130     else if (X > T->Element)
131     {
132         T->Right = Delete(X, T->Right);//向右查找
133     }
134     else if (T->Left&&T->Right)//找到右子树最小值替换
135     {
136         TmpCell = FindMin(T->Right);
137         T->Element = TmpCell->Element;
138         T->Right = Delete(T->Element, T->Right);
139     }
140     else
141     {
142         TmpCell = T;
143         if (T->Left == NULL)
144         {
145             T = T->Right;
146         }
147         else if (T->Right == NULL)
148         {
149             T = T->Left;
150         }
151         free(TmpCell);
152     }
153     return  T;
154 }
155 
156 void main()
157 {
158     SearchTree T=NULL;
159     T = Insert(5, T);
160     T = Insert(2, T);
161     T = Insert(1, T);
162     T = Insert(8, T);
163     
164     printf("%d", T->Left->Element);
165     printf("%d", T->Right->Element);
166     printf("%d",FindMax(T)->Element);
167     char i;
168     scanf("%c", &i);
169 }

AVL树

AVL树是带有平衡条件的二叉查找树。这个平衡条件必须要容易保持，而且必须保证树的深度O(logN)。最简单的想法是要求左右子树具有相同高度。 
另一种平衡条件是要求每个节点都必须有相同高度的左子树和右子树。 
下面的例子中，是左右每个节点的左子树和右子树最多差1的AVL树。 
不平衡可能出现在下面四种情况：（a为节点）

• 对a的左儿子的左子树进行一次插入
• 对a的左儿子的右子树进行一次插入
• 对a的右儿子的左子树进行一次插入
• 对a的右儿子的右子树进行一次插入 
  1，4通过一次单旋转可以完成调整 
  2，3通过一次双旋转可以完成调整 
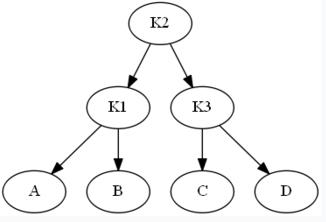
  单旋转调整过程如下图：

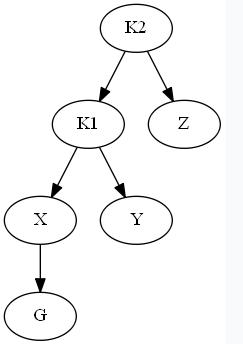
此时，K2的左子树深度为3，右子树深度为1 
下图为调整后图：

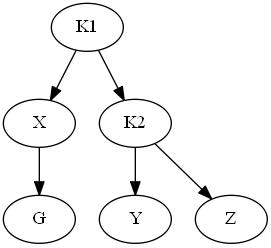
双旋转调整过程如下图：

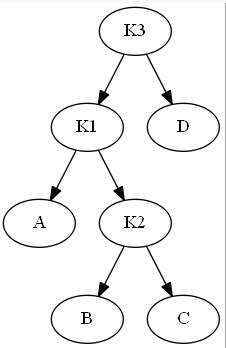
调整后：

  1 #include <stdio.h>
  2 #include <windef.h>
  3 struct AvlNode;
  4 
  5 typedef  struct  AvlNode *Position;
  6 typedef  struct  AvlNode *AvlTree;
  7 
  8 struct AvlNode
  9 {
 10     int Element;
 11     AvlTree Left;
 12     AvlTree Right;
 13     int Height;
 14 };
 15 
 16 static int Max(int x,int y)
 17 {
 18     if (x>y)
 19     {
 20         return x;
 21     }
 22     else
 23     {
 24         return y;
 25     }
 26 }
 27 
 28 static int Height(Position P)
 29 {
 30     if (P==NULL)
 31     {
 32         return -1;
 33     }
 34     else
 35     {
 36         return P->Height;
 37     }
 38 }
 39 
 40 //左旋转（单）
 41 static Position SingleRotateWithLeft(Position K2)
 42 {
 43     Position K1;
 44 
 45     K1 = K2->Left;
 46     K2->Left = K1->Right;
 47     K1->Right = K2;
 48 
 49     K2->Height = Max(Height(K2->Left), Height(K2->Right)) + 1;
 50 
 51     K1->Height = Max(Height(K1->Left), K2->Height) + 1;
 52 
 53     return K1;
 54 }
 55 
 56 //左旋转（双）
 57 static Position DoubleRotateWithLeft(Position K3)
 58 {
 59     K3->Left = SingleRotateWithRight(K3->Left);
 60     return SingleRotateWithLeft(K3);
 61 }
 62 
 63 
 64 //插入
 65 AvlTree Insert(int X, AvlTree T)
 66 {
 67     if (T == NULL) {
 68         T = malloc(sizeof(struct AvlNode));
 69         if (T == NULL)
 70         {
 71             FatalError("Error");
 72         }
 73         else
 74         {
 75             T->Element = X;
 76             T->Height = 0;
 77             T->Left = T->Right = NULL;
 78         }
 79     }
 80     else if (X<T->Element)
 81     {
 82         T->Left = Insert(X, T->Left);
 83         if (Heigth(T->Left)-Height(T->Right)==2)//是否超过平衡高度
 84         {
 85             if (X < T->Left->Element) {
 86                 T = SingleRotateWithLeft(T);
 87             }
 88             else
 89             {
 90                 T = DoubleRotateWithLeft(T);
 91             }
 92         }
 93     }
 94     else if (X>T->Element)
 95     {
 96         T->Right = Insert(X, T->Right);
 97         if (Heigth(T->Right)-Height(T->Left)==2)
 98         {
 99             if (X>T->Right->Element)
100             {
101                 T = SingleRotateWithRight(T);
102             }
103             else
104             {
105                 T = DoubleRotateWithRight(T);
106             }
107         }
108     }
109     T->Height = Max(Height(T->Left), Height(T->Right)) + 1;
110     return T;
111 }

伸展树

它保证从空树开始任意连续M次对树的操作最多花费O（MlogN）的时间。在这其中不排除某一次操作花费O（N）时间。当M次操作的序列总的最坏情形运行时间为O（MF(N)）时，我们就说它的摊还运行时间为O(F（N）)。 
伸展树基于这样的事实：对于二叉树来说，每次操作最坏情形的时间O(N)并不坏，只要不常发生就可以了，但对于一系列访问，每次都花费最坏情形就不如人意了。 
伸展树的基本想法：当一个节点被访问后，它要经过一系列AVL树的旋转被放到根上。 
对下面一颗二叉树k1进行一次访问：

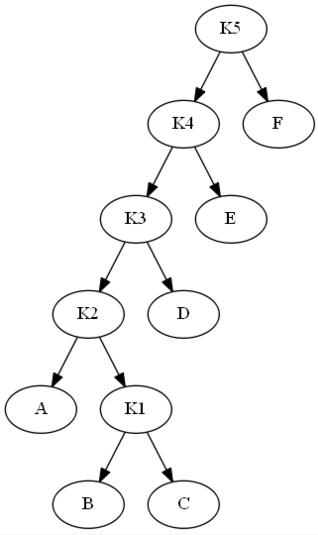
对K1和它的父节点之间实施一次单旋转：

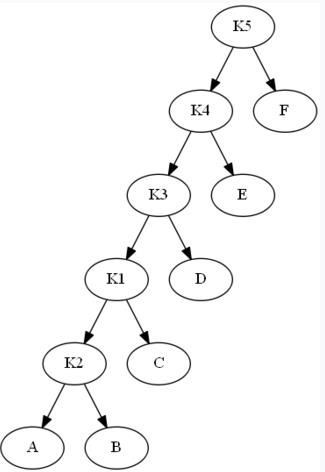
K1和K3间旋转：

 

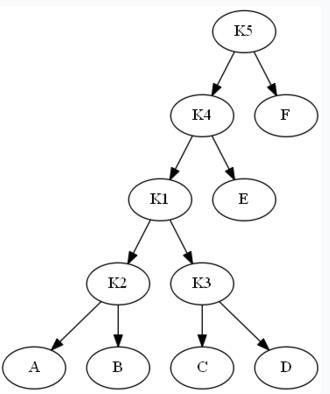
K1和K4间旋转：

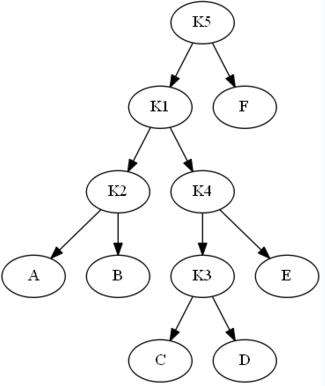
K1和K5旋转：

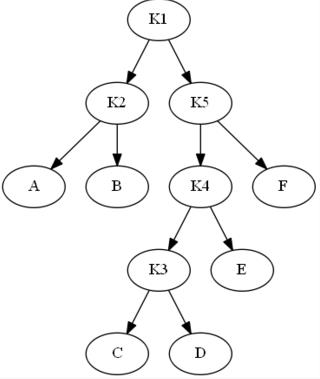
B-树

B-树在实际应用中，被用于数据库系统，在那里树被存储在物理的磁盘上而不是主存中。 
下面，就来基本了解下B-树 
B-树不是二叉树 
阶为M的B-树是一颗具有下列结构特性的树：

• 树的根或者一片树叶，或其儿子数在2和M之间。
• 除根外，所有非树叶节点的儿子数在[M/2]和M之间。
• 所有的树叶都在相同的深度上。 
  B-树所有数据都存储在树叶上，在一个内部节点上皆含有指向该节点各儿子的指针P1,P2…..PM和分别代表在子树P2,P3….PM中发现的最小关键字的值K1,K2…KM.指针是NULL，那么Ki未定义。对于每一个节点，其子树P1中所有关键字都小于子树P2中所有关键字。 

 下图是一颗3阶B-树：（之前使用的工具无法画出B-树，这里改用下另一个）

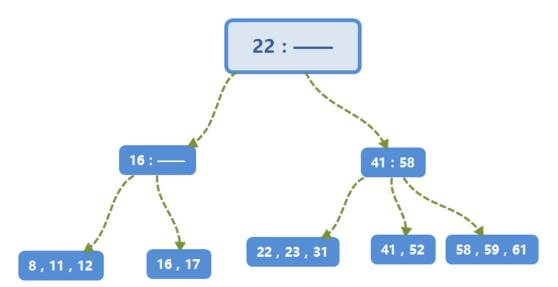
对于一般的M阶B树，当插入一个关键字时，唯一的困难发生在接收该关键字的节点已经具有M个关键字的时候。这个关键字使得该节点具有M+1个关键字，我们就可以把它分裂成两个节点，它们分别具有[(M+1)/2]个和[(M+1)/2]个关键字。由于这使得父节点多出一个儿子，因此又要再次检测可否被父节点接受，如果不能，父节点再次分裂。