机器学习实战之kNN算法
Posted 笨鸟多学
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习实战之kNN算法相关的知识,希望对你有一定的参考价值。
机器学习实战这本书是基于python的,如果我们想要完成python开发,那么python的开发环境必不可少:
(1)python3.52,64位,这是我用的python版本
(2)numpy 1.11.3,64位,这是python的科学计算包,是python的一个矩阵类型,包含数组和矩阵,提供了大量的矩阵处理函数,使运算更加容易,执行更加迅速。
(3)matplotlib 1.5.3,64位,在下载该工具时,一定要对应好python的版本,处理器版本,matplotlib可以认为是python的一个可视化工具
好了,如果你已经完成了上述的环境配置,下面就可以开始完成真正的算法实战了。
一,k近邻算法的工作原理:
存在一个样本数据集,也称作训练数据集,并且样本集中每个数据都存在标签,即我们知道样本集中每个数据与所属分类的对应关系。当输入没有标签的新数据后,将新数据的每个特征与样本集中数据对应的特征进行比较,然后算法提取样本集中特征最相似的数据的分类标签。一般来水,我们只选择样本数据集中最相似的k个数据(通常k不大于20),再根据多数表决原则,选择k个最相似数据中出现次数最多的分类,作为新数据的分类。
k近邻算法的一般流程:
(1)收集数据:可以采用公开的数据源
(2)准备数据:计算距离所需要的数值
(3)分析数据:剔除垃圾信息
(4)测试算法:计算错误率
(5)使用算法:运用在实际中,对实际情况进行预测
二,算法具体实施过程
(1)使用python导入数据,代码解析如下:
#-------------------------1 准备数据------------------------------- #可以采用公开的数据集,也可以利用网络爬虫从网站上抽取数据,方式不限 #-------------------------2 准备数据------------------------------- #确保数据格式符合要求 #导入科学计算包(数组和矩阵) from numpy import * from os import listdir #导入运算符模块 import operator #创建符合python格式的数据集 def createDataSet(): #数据集 list(列表形式) group=array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]]) #标签 labels=[\'A\',\'A\',\'B\',\'B\'] return group, labels
(2)我们可以使用matplotlib 对数据进行分析
在python命令环境中,输入如下命令:
当输入如下命令时:
#导入制图工具 import matplotlib import matplotlib.pyplot as plt fig=plt.figure() ax=fig.add_subplot(111) ax.scatter(datingDataMat[:,1],datingDataMat[:,2]) plt.show()
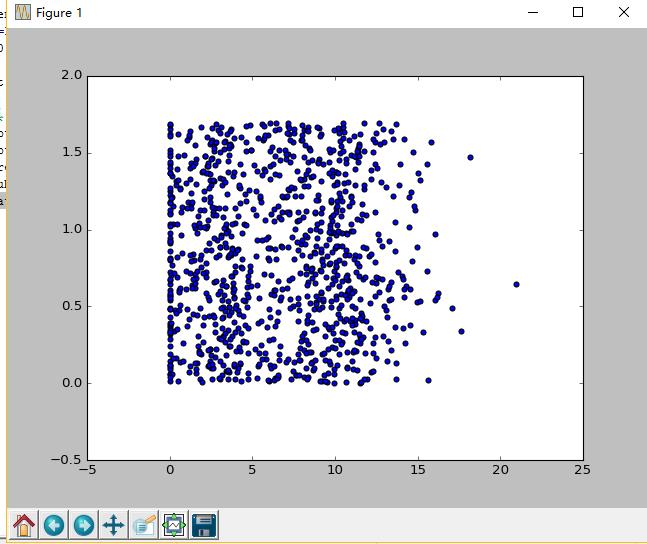
从上面可以看到,由于没有使用样本分类的特征值,我们很难看到比较有用的数据模式信息
一般而言,我们会采用色彩或其他几号来标记不同样本的分类,以便更好的理解数据,重新输入命令:
#导入制图工具 import matplotlib import matplotlib.pyplot as plt fig=plt.figure() ax=fig.add_subplot(111) #记得导入array函数 from numpy import array #色彩不等,尺寸不同 ax.scatter(datingDataMat[:,1],datingDataMat[:,2],15.0*array(datingLabels),15.0*array(datingLabels)) plt.show()

(3)实施kNN算法
k近邻算法对未知类别属性的数据集中每个点依次执行如下步骤:
1)计算已知类别数据集中的点与当前点之间的距离
2)按照距离递增次序排序
3)选取与当前点距离最小的k个点
4)确定前k个点所在类别的出现频率
5)返回前k个点出现频率最高的类别作为当前点的预测分类
具体代码解析如下:
#-------------------------构建分类器------------------------------- #KNN算法实施 #@inX 测试样本数据 #@dataSet 训练样本数据 #@labels 测试样本标签 #@k 选取距离最近的k个点 def classify0(inX,dataSet,labels,k): #获取训练数据集的行数 dataSetSize=dataSet.shape[0] #---------------欧氏距离计算----------------- #各个函数均是以矩阵形式保存 #tile():inX沿各个维度的复制次数 diffMat=tile(inX,(dataSetSize,1))-dataSet sqDiffMat=diffMat**2 #.sum()运行加函数,参数axis=1表示矩阵每一行的各个值相加和 sqDistances=sqDiffMat.sum(axis=1) distances=sqDistances**0.5 #-------------------------------------------- #获取排序(有小到大)后的距离值的索引(序号) sortedDistIndicies=distances.argsort() #字典,键值对,结构类似于hash表 classCount={} for i in range(k): #获取该索引对应的训练样本的标签 voteIlabel=labels[sortedDistIndicies[i]] #累加几类标签出现的次数,构成键值对key/values并存于classCount中 classCount[voteIlabel]=classCount.get(voteIlabel,0)+1 #将字典列表中按照第二列,也就是次数标签,反序排序(由大到小排序) sortedClassCount=sorted(classCount.items(), key=operator.itemgetter(1),reverse=True) #返回第一个元素(最高频率)标签key return sortedClassCount[0][0]
(3)测试分类器
下面以两个实例对分类器效果进行测试
实例1:使用kNN改进某约会网站的配对效果
#-------------------------knn算法实例----------------------------------- #-------------------------约会网站配对----------------------------------- #---------------1 将text文本数据转化为分类器可以接受的格式--------------- def file2matrix(filename): #打开文件 fr=open(filename) #读取文件每一行到array0Lines列表 #read():读取整个文件,通常将文件内容放到一个字符串中 #readline():每次读取文件一行,当没有足够内存一次读取整个文件内容时,使用该方法 #readlines():读取文件的每一行,组成一个字符串列表,内存足够时使用 array0Lines=fr.readlines() #获取字符串列表行数行数 numberOfLines=len(array0Lines) #返回的特征矩阵大小 returnMat=zeros((numberOfLines,3)) #list存储类标签 classLabelVector=[] index=0 for line in array0Lines: #去掉字符串头尾的空格,类似于Java的trim() line=line.strip() #将整行元素按照tab分割成一个元素列表 listFromLine=line.split(\'\\t\') #将listFromLine的前三个元素依次存入returnmat的index行的三列 returnMat[index,:]=listFromLine[0:3] #python可以使用负索引-1表示列表的最后一列元素,从而将标签存入标签向量中 #使用append函数每次循环在list尾部添加一个标签值 classLabelVector.append(int(listFromLine[-1])) index+=1 return returnMat,classLabelVector #----------------2 准备数据:归一化---------------------------------------------- #计算欧式距离时,如果某一特征数值相对于其他特征数值较大,那么该特征对于结果影响要 #远大于其他特征,然后假设特征都是同等重要,即等权重的,那么可能某一特征对于结果存 #在严重影响 def autoNorm(dataSet): #找出每一列的最小值 minVals=dataSet.min(0) #找出每一列的最大值 maxVals=dataSet.max(0) ranges=maxVals-minVals #创建与dataSet等大小的归一化矩阵 #shape()获取矩阵的大小 normDataSet=zeros(shape(dataSet)) #获取dataSet第一维度的大小 m=dataSet.shape[0] #将dataSet的每一行的对应列减去minVals中对应列的最小值 normDataSet=dataSet-tile(minVals,(m,1)) #归一化,公式newValue=(value-minvalue)/(maxVal-minVal) normDataSet=normDataSet/tile(ranges,(m,1)) return normDataSet,ranges,minVals #-------------------------3 测试算法---------------------------------------------- #改变测试样本占比,k值等都会对最后的错误率产生影响 def datingClassTest(): #设定用来测试的样本占比 hoRatio=0.10 #从文本中提取得到数据特征,及对应的标签 datingDataMat,datingLabels=file2matrix(\'datingTestSet2.txt\') #对数据特征进行归一化 normMat,ranges,minVals=autoNorm(datingDataMat) #得到第一维度的大小 m=normMat.shape[0] #测试样本数量 numTestVecs=int(hoRatio*m) #错误数初始化 errorCount=0.0 for i in range(numTestVecs): #利用分类函数classify0获取测试样本数据分类结果 classifierResult=classify0(normMat[i,:],normMat[numTestVecs:m,:],\\ datingLabels[numTestVecs:m],3) #打印预测结果和实际标签 print("the classifier came back with: %d, the real answer is: %d"\\ %(classifierResult,datingLabels[i])) #如果预测输出不等于实际标签,错误数增加1.0 if(classifierResult != datingLabels[i]):errorCount+=1.0 #打印最后的误差率 print("the total error rate is: %f" %(errorCount/float(numTestVecs))) #-------------------------4 构建可手动输入系统------------------------------------ #用户输入相关数据,进行预测 def classifyPerson(): #定义预测结果 resultList=[\'not at all\',\'in small does\',\'in large does\'] #在python3.x中,已经删除raw_input(),取而代之的是input() percentTats=float(input(\\ "percentage of time spent playing video games?")) ffMiles=float(input("frequent filer miles earned per year?")) iceCream=float(input("liters of ice cream consumed per year?")) datingDataMat,datingLabels=file2matrix(\'datingTestSet2.txt\') normMat,ranges,minValues=autoNorm(datingDataMat) #将输入的数值放在数组中 inArr=array([ffMiles,percentTats,iceCream]) classifierResult=classify0((inArr-minValues)/ranges,normMat,datingLabels,3) print("you will probably like this person:",resultList[classifierResult-1])
实验结果:

当然用户也可以自己手动输入,进行预测:
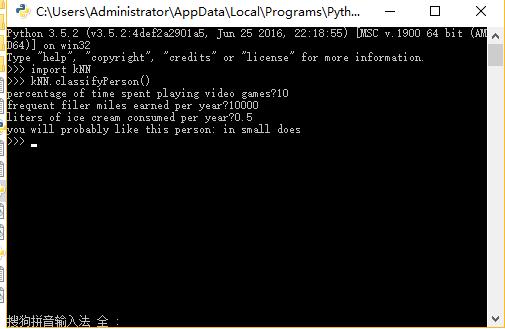
实例2 手写识别系统
#-------------------------knn算法实例----------------------------------- #-------------------------手写识别系统----------------------------------- #-------------------------1 将图像转化为测试向量------------------------- #图像大小32*32,转化为1024的向量 def img2vector(filename): returnVec=zeros((1,1024)) fr=open(filename) for i in range(32): #每次读取一行 lineStr=fr.readline() for j in range(32): #通俗讲:就是根据首地址(位置)的偏移量计算出当前数据存放的地址(位置) returnVec[0,32*i+j]=int(lineStr[j]) return returnVec #-------------------------2 测试代码-------------------------------------- def handwritingClassTest(): hwLabels=[] #列出给定目录的文件名列表,使用前需导入from os import listdir trainingFileList=listdir(\'knn/trainingDigits\') #获取列表的长度 m=len(trainingFileList) #创建一个m*1024的矩阵用于存储训练数据 trainingMat=zeros((m,1024)) for i in range(m): #获取当前行的字符串 fileNameStr=trainingFileList[i] #将字符串按照\'.\'分开,并将前一部分放于fileStr fileStr=fileNameStr.split(\'.\')[0] #将fileStr按照\'_\'分开,并将前一部分存于classNumStr classNumStr=int(fileStr.split(\'_\')[0]) #将每个标签值全部存入一个列表中 hwLabels.append(classNumStr) #解析目录中的每一个文件,将图像转化为向量,最后存入训练矩阵中 trainingMat[i,:]=img2vector(\'knn/trainingDigits/%s\' %fileNameStr) #读取测试数据目录中的文件列表 testFileList=listdir(\'knn/testDigits\') errorCount=0.0 mTest=len(testFileList) for i in range(mTest): #获取第i行的文件名 fileNameStr=testFileList[i] #将字符串按照\'.\'分开,并将前一部分放于fileStr fileStr=fileNameStr.split(\'.\')[0] #将fileStr按照\'_\'分开,并将前一部分存于classNumStr classNumStr=int(fileStr.split(\'_\')[0]) #解析目录中的每一个文件,将图像转化为向量 vectorUnderTest=img2vector(\'knn/testDigits/%s\' %fileNameStr) #分类预测 classifierResult=classify0(vectorUnderTest,trainingMat,hwLabels,3) #打印预测结果和实际结果 print("the classifierResult came back with: %d,the real answer is: %d" %(classifierResult,classNumStr)) #预测错误,错误数加1次 if(classifierResult!=classNumStr):errorCount+=1.0 #打印错误数和错误率 print("\\nthe total number of errors is: %d" %errorCount) print("\\nthe total error rate is: %f" %(errorCount/float(mTest)))
实验结果(错误率):
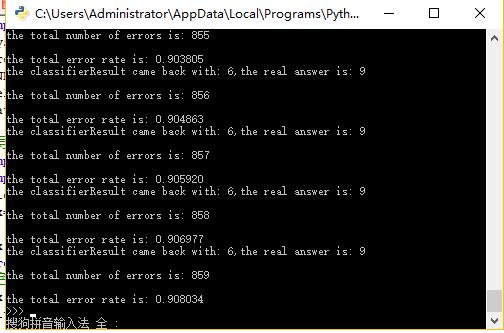
三,算法小结:
(1) 如果我们改变训练样本的数目,调整相应的k值,都会对最后的预测错误率产生影响,我们可以根据错误率的情况,对这些变量进行调整,从而降低预测错误率
(2)k近邻算法的优缺点:
k近邻算法具有精度高,对异常值不敏感的优点
k近邻算法是基于实例的学习,使用算法时我们必须有接近实际数据的训练样本数据。k近邻算法必须保存全部数据集,如果训练数据集很大,必须使用大量的存储空间。此外,由于必须对数据集中的每个数据计算距离,实际使用时也可能会非常耗时
此外,k近邻算法无法给出数据的基础结构信息,因此我们无法知道平均实例样本和典型实例样本具有怎样的特征。
以上是关于机器学习实战之kNN算法的主要内容,如果未能解决你的问题,请参考以下文章
阿旭机器学习实战33中文文本分类之情感分析--朴素贝叶斯KNN逻辑回归
机器学习实战☛k-近邻算法(K-Nearest Neighbor, KNN)