[BZOJ 1502][NOI2005]月下柠檬树（自适应Simpson积分）

Posted 2020-09-11 Zars19

Description

李哲非常非常喜欢柠檬树,特别是在静静的夜晚,当天空中有一弯明月温柔地照亮地面上的景物时,他必会悠闲地坐在他亲手植下的那棵柠檬树旁,独自思索着人生的哲理。
李哲是一个喜爱思考的孩子,当他看到在月光的照射下柠檬树投在地面上的影子是如此的清晰,马上想到了一个问题:树影的面积是多大呢?
李哲知道,直接测量面积是很难的,他想用几何的方法算,因为他对这棵柠檬树的形状了解得非常清楚,而且想好了简化的方法。
李哲将整棵柠檬树分成了 n 层,由下向上依次将层编号为 1,2,...,n。从第 1到 n-1 层,每层都是一个圆台型,第 n 层(最上面一层)是圆锥型。对于圆台型,其上下底面都是水平的圆。对于相邻的两个圆台,上层的下底面和下层的上底面重合。第 n 层(最上面一层)圆锥的底面就是第 n-1 层圆台的上底面。所有的底面的圆心(包括树顶)处在同一条与地面垂直的直线上。李哲知道每一层的高度为h1,h2,...,hn,第 1 层圆台的下底面距地面的高度为 h0,以及每层的下底面的圆的半径 r1,r2,...,rn。李哲用熟知的方法测出了月亮的光线与地面的夹角为 alpha。

Solution

本来只是想顺手找道计算几何做，结果被虐虐虐虐虐…细节杀*2

平行光在圆上的投影还是它本身的样子，于是变成了一堆圆和相邻圆的公切线组成的图形（还有一个尖顶）

得到了一个类似这样的东西

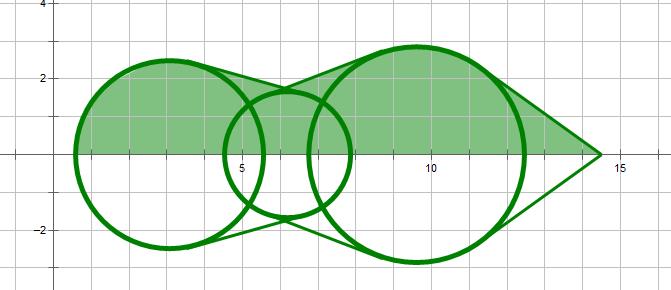
可以用辛普森积分算它一半的面积

具体实现什么的还是见代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#define pi acos(-1)
using namespace std;
int n;
double alpha,h[505];
struct point{
    double x,y;
    point(double x=0,double y=0):x(x),y(y){}
}line[505][2];
struct circle{
    point c;double r;
    circle(point c=point(0,0),double r=0):c(c),r(r){}
    point getpoint(double ang){
        return point(c.x+r*cos(ang),c.y+r*sin(ang));
    }
}lemon[505];
void getline(circle a,circle b,point& p,point& q)
{
    if(a.r<b.r)swap(a,b);
    if((a.r-b.r)>=fabs(a.c.x-b.c.x))return;
    double ang=acos((a.r-b.r)/fabs(a.c.x-b.c.x));
    if(a.c.x<=b.c.x)p=a.getpoint(ang),q=b.getpoint(ang);
    else q=a.getpoint(pi-ang),p=b.getpoint(pi-ang);
}
double pow(double x){return x*x;}
double f(double x)
{
    double res=0;
    for(int i=0;i<n;i++)
    if(line[i][0].x<=x&&line[i][1].x>=x){
        res=max(res,(x-line[i][0].x)*(line[i][1].y-line[i][0].y)/(line[i][1].x-line[i][0].x)+line[i][0].y);
    }
    for(int i=0;i<=n;i++){
        if(pow(lemon[i].r)-pow(lemon[i].c.x-x)>=0)
        res=max(res,sqrt(pow(lemon[i].r)-pow(lemon[i].c.x-x)));
    }
    return res;
}
double simpson(double a,double b){
    double c=a+(b-a)/2;
    return (f(a)+4*f(c)+f(b))*(b-a)/6;
}
double asr(double a,double b,double eps,double A){
    double c=a+(b-a)/2;
    double l=simpson(a,c),r=simpson(c,b);
    if(fabs(l+r-A)<=15*eps)return l+r+(l+r-A)/15.0;
    return asr(a,c,eps/2,l)+asr(c,b,eps/2,r);
}
double asr(double a,double b,double eps){
    return asr(a,b,eps,simpson(a,b));
}
int main()
{
    scanf("%d%lf",&n,&alpha);
    double s=0;
    for(int i=0;i<=n;i++){
        scanf("%lf",&h[i]);
        s+=h[i];
        h[i]=s/tan(alpha);
    }
    double r,minn=1000000000,maxn=0;
    for(int i=0;i<=n;i++){
        if(i!=n)scanf("%lf",&r);
        else r=0;
        maxn=max(maxn,h[i]+r);
        minn=min(minn,h[i]-r);
        lemon[i]=circle(point(h[i],0),r);
    }
    for(int i=0;i<n;i++){
        getline(lemon[i],lemon[i+1],line[i][0],line[i][1]);
    }
    printf("%.2lf\\n",2*asr(minn,maxn,1e-7));
    return 0;
} 

And all that I can see.
And all that I can see.
And all that I can see is just a lemon tree.