本福特定律

Posted 2020-09-09

本福特定律

测试结果

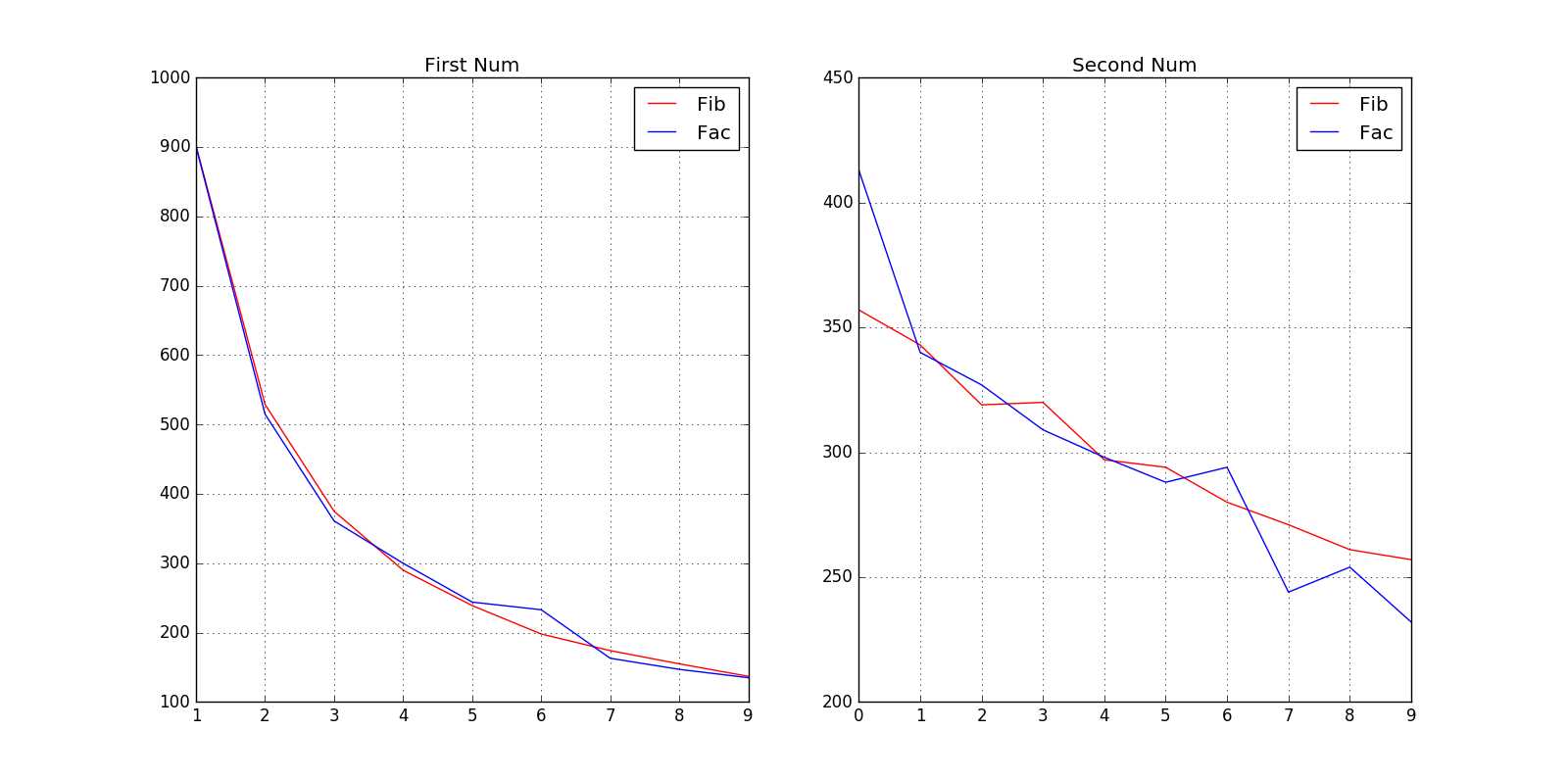
比例

1 : 30.0766922307

2 : 17.639213071

3 : 12.504168056

4 : 9.66988996332

5 : 7.9693231077

6 : 6.60220073358

7 : 5.80193397799

8 : 5.16838946315

9 : 4.56818939647

附代码

# -*- coding: utf-8 -*-
"""
Created on Mon Apr 03 23:31:14 2017
@author: LoveDMR
本福特定律实验  Benford
"""
import matplotlib.pyplot as plt
def first_num( n ):
    while( n / 10 > 0 ):
        n = n / 10
    return n 
    
def second_num( n ):
    while( n / 100 > 0 ):
        n = n / 10
    return n%10
if __name__ == ‘__main__‘:
    fib_first = [ 0 ] * 10
    fib_second = [ 0 ] * 10
    fac_first = [ 0 ] * 10
    fac_second = [ 0 ] * 10
    a , b = 1,1
    k = 1
    for i in range(1,3000):
        # 斐波那契数列
        a , b = b , a + b
        first_fib = first_num( a )
        second_fib = second_num( a )
        fib_first[first_fib] = fib_first[first_fib] + 1
        fib_second[second_fib] = fib_second[second_fib] + 1
        # 阶乘
        k *= i
        first_fac = first_num( k )
        second_fac = second_num( k )
        fac_first[first_fac] = fac_first[first_fac] + 1
        fac_second[second_fac] = fac_second[second_fac] + 1
    
    for n , i in enumerate(fib_first[1:],1):
        print n , ":" , i * 100.0 / sum(fib_first[1:])
        
    plt.figure( figsize =( 16, 8 ) )
    plt.subplot(121)
    plt.plot( range(1,10) , fib_first[1:] , ‘r-‘ , label=‘Fib‘)
    plt.plot( range(1,10) , fac_first[1:] , ‘b-‘ ,label=‘Fac‘)
    plt.title(‘First Num‘)
    plt.legend()
    plt.grid()
    plt.subplot(122)
    plt.plot( range(0,10) , fib_second , ‘r-‘ , label=‘Fib‘)
    plt.plot( range(0,10) , fac_second , ‘b-‘ , label=‘Fac‘)
    plt.title(‘Second Num‘)
    plt.legend()
    plt.grid()
    plt.show()