直方图均衡化原理与实现
Posted HUSTLX
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了直方图均衡化原理与实现相关的知识,希望对你有一定的参考价值。
直方图均衡化(Histogram Equalization) 又称直方图平坦化,实质上是对图像进行非线性拉伸,重新分配图像象元值,使一定灰度范围内象元值的数量大致相等。这样,原来直方图中间的峰顶部分对比度得到增强,而两侧的谷底部分对比度降低,输出图像的直方图是一个较平的分段直方图:如果输出数据分段值较小的话,会产生粗略分类的视觉效果。
直方图是表示数字图像中每一灰度出现频率的统计关系。直方图能给出图像灰度范围、每个灰度的频度和灰度的分布、整幅图像的平均明暗和对比度等概貌性描述。灰度直方图是灰度级的函数, 反映的是图像中具有该灰度级像素的个数, 其横坐标是灰度级r, 纵坐标是该灰度级出现的频率( 即像素的个数) pr( r) , 整个坐标系描述的是图像灰度级的分布情况, 由此可以看出图像的灰度分布特性, 即若大部分像素集中在低灰度区域, 图像呈现暗的特性; 若像素集中在高灰度区域, 图像呈现亮的特性。
图1所示就是直方图均衡化, 即将随机分布的图像直方图修改成均匀分布的直方图。基本思想是对原始图像的像素灰度做某种映射变换, 使变换后图像灰
度的概率密度呈均匀分布。这就意味着图像灰度的动态范围得到了增加, 提高了图像的对比度。
图1 直方图均衡化
通过这种技术可以清晰地在直方图上看到图像亮度的分布情况, 并可按照需要对图像亮度调整。另外,这种方法是可逆的, 如果已知均衡化函数, 就可以恢复原始直方图。
设变量r 代表图像中像素灰度级。对灰度级进行归一化处理, 则0≤r≤1, 其中r= 0表示黑, r= 1表示白。对于一幅给定的图像来说, 每个像素值在[ 0,1] 的灰度级是随机的。用概率密度函数![]() 来表示图像灰度级的分布。
来表示图像灰度级的分布。
为了有利于数字图像处理, 引入离散形式。在离散形式下, 用![]() 代表离散灰度级, 用
代表离散灰度级, 用![]() 代表
代表![]() , 并且下式成立:
, 并且下式成立:![]()
其中, 0≤![]() ≤1, k=0, 1, 2, …, n-1。式中
≤1, k=0, 1, 2, …, n-1。式中![]() 为图像中出现
为图像中出现![]() 这种灰度的像素数, n是图像中的像素总数, 而
这种灰度的像素数, n是图像中的像素总数, 而![]() 就是概率论中的频数。图像进行直方图均衡化的函数表达式为:
就是概率论中的频数。图像进行直方图均衡化的函数表达式为:
式中, k为灰度级数。相应的反变换为:
四、算法实现及结果分析
4.1核心算法
#define HDIM 256
#define SRC 0
#define DST 1
int main(int argc, char** argv)
{
IplImage *src = 0, *dst = 0;
int n[] = {HDIM,HDIM,HDIM};
int r[256] = {0}, g[256] = {0}, b[256] = {0};
if(argc!=2 || (src = cvLoadImage(argv[1],3))== NULL) return -1;
cvNamedWindow("source",1);
cvNamedWindow("result",1);
int width = src->width;
int height = src->height;
int sum = width * height; //图像中的像素点综合
int i,j;
//分别统计直方图的RGB分布
for(i=0; i<height; i++)
for(j=0; j<width; j++)
{
b[((uchar*)(src->imageData+i*src->width))[j*src->nChannels+0]]++;
g[((uchar*)(src->imageData+i*src->width))[j*src->nChannels+1]]++;
r[((uchar*)(src->imageData+i*src->width))[j*src->nChannels+2]]++;
}
////构建直方图的累计分布方程,用于对直方图进行均衡化
double val[3] = {0};
for(i=0; i<HDIM; i++)
{
val[0] += b[i];
val[1] += g[i];
val[2] += r[i];
b[i] = val[0]*255/sum;
g[i] = val[1]*255/sum;
r[i] = val[2]*255/sum;
}
dst = cvCreateImage(cvSize(width,height),8,3);
//归一化直方图
for(i=0; i<height; i++)
for(j=0; j<width; j++)
{
((uchar*)(dst->imageData+i*dst->widthStep))[j*dst->nChannels+0]=b[((uchar*)(src->imageData+i*src->widthStep))[j*src->nChannels+0]];
((uchar*)(dst->imageData+i*dst->widthStep))[j*dst->nChannels+1]=g[((uchar*)(src->imageData+i*src->widthStep))[j*src->nChannels+1]];
((uchar*)(dst->imageData+i*dst->widthStep))[j*dst->nChannels+2]=r[((uchar*)(src->imageData+i*src->widthStep))[j*src->nChannels+2]];
}
cvShowImage("source",src);
cvShowImage("result",dst);
cvSaveImage("out.jpg",dst);
cvWaitKey(0);
cvDestroyWindow("source");
cvDestroyWindow("result");
cvReleaseImage(&src);
cvReleaseImage(&dst);
cvReleaseHist(&hist);
return 0;
}
4.2结果展示
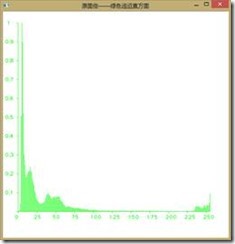
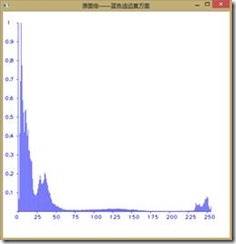
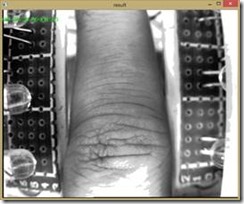
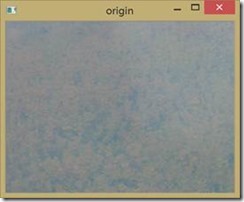
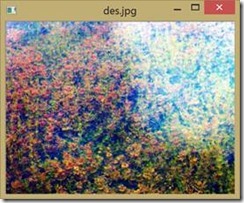
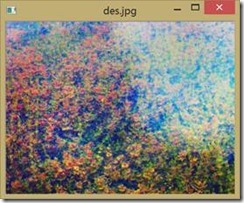
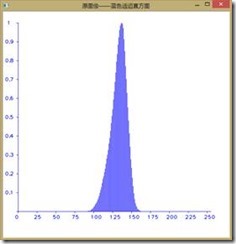
对于第一幅图像,首先我们在RGB空间对其进行直方图均衡化得如下结果:
可见右上角由较大的光影,我们对其进行同台滤波,如下图所示,但是效果也不太好。
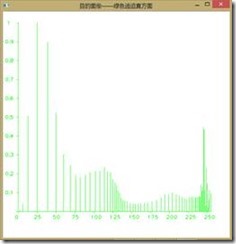
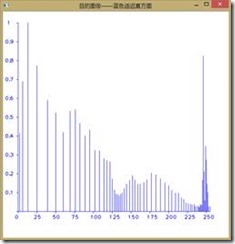
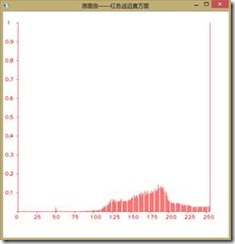
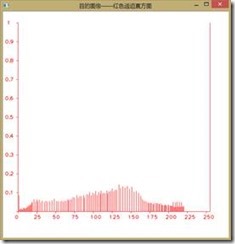
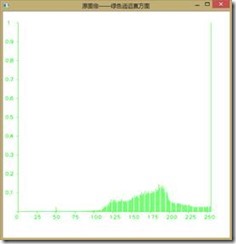
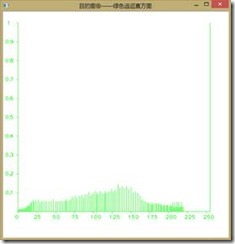
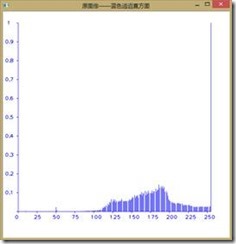
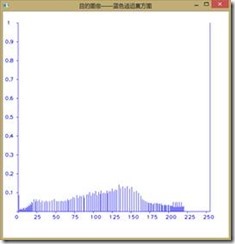
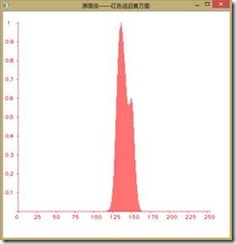
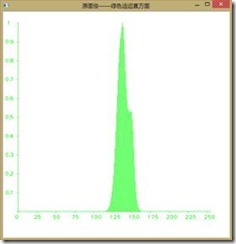
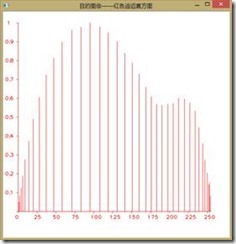
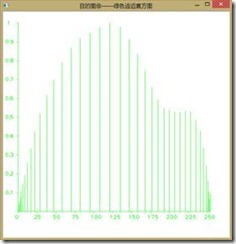
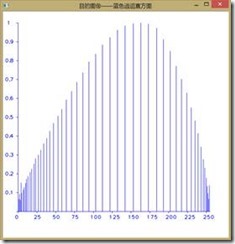
如下图所示为直方图均衡前后图像RGB分量的直方图,可以看到收到了较好的效果,由于直方图均衡第二个作业已经做过,我们在此不再赘述。
对于HSI空间的直方图均衡化,首先我们要进行RGB和HIS空间颜色分量的转化,代码如下:
/**************************************************************
函数功能:对图像进行由RGB空间到HSI空间的转化
输入参数:源图像src;目标图像des;图像参数width,height,nChannels;
输出参数:目标图像
**************************************************************/
void rgb_hsi(unsigned char* des, const unsigned char* src, int width, int height, int nChannels)
{
for(int y=0; y<height; y++)
{
for (int x=0; x<width; x++)
{
double B= src[y * width * nChannels + x * nChannels ] ;
double G= src[y * width * nChannels + x * nChannels + 1] ;
double R= src[y * width * nChannels + x * nChannels + 2] ;
double H,S,I=0;//H色调、S饱和度(纯度)、I强度
double mx,mi;
mx=max(max(R,G),B);
mi=min(min(R,G),B);
if (mx==mi) //如果RGB相等
{
k=k+1;
H=0; //H分量为0
S=0; //S分量为0
I=mi;
}
else
{
if (B<=G)
{
H=acos((0.5*((R-B)+(R-G)))/(sqrt(1.0*((R-G)*(R-G)+(R-B)*(G-B)))));
}
else
{
H=360-acos((0.5*((R-B)+(R-G)))/(sqrt(1.0*((R-G)*(R-G)+(R-B)*(G-B)))));
}
S=(3*mi)/(R+B+G);
S=1-S;
I=(R+B+G)/3;
}
des[y * width * nChannels + x * nChannels + 0]= int(H);
des[y * width * nChannels + x * nChannels + 1]= int (S*255);
des[y * width * nChannels + x * nChannels + 2]=int(I);
}
}
}
/**************************************************************
函数功能:对图像进行由HSI空间到RGB空间的转化
输入参数:源图像src;目标图像des;图像参数width,height,nChannels;
输出参数:目标图像
**************************************************************/
void hsi_rgb(unsigned char* des, const unsigned char* src, int width, int height, int nChannels)
{
for(int y=0; y<height; y++)
{
for (int x=0; x<width; x++)
{
double H= src[y * width * nChannels + x * nChannels ] ;
//printf("H%d",H);
double S= src[y * width * nChannels + x * nChannels + 1]/255 ;
//printf("S%d",S);
double I= src[y * width * nChannels + x * nChannels + 2] ;
//printf("I%d",I);
double R,G,B;//H色调、S饱和度(纯度)、I强度
if((H>=0)&&(H<120))
{
B=I*(1-S);
R=I*(1+S*cos(H)/cos(60-H));
G=3*I-(R+B);
}
else if((H>=120)&&(H<240))
{
H=H-120;
R=I*(1-S);
G=I*(1+S*cos(H)/cos(60-H));
B=3*I-(R+G);
}
else
{
H=H-240;
G=I*(1-S);
B=I*(1+S*cos(H)/cos(60-H));
R=3*I-(B+G);
}
des[y * width * nChannels + x * nChannels + 0]= int(B);
des[y * width * nChannels + x * nChannels + 1]= int(G);
des[y * width * nChannels + x * nChannels + 2]= int(R);
for(int n=0;n<nChannels;n++)
{
int val=des[y * width * nChannels + x * nChannels + n];
if(val<0)
des[y * width * nChannels + x * nChannels + n]=0;
else if(val>255)
des[y * width * nChannels + x * nChannels + n]=255;
else
des[y * width * nChannels + x * nChannels + n]=des[y * width * nChannels + x * nChannels + n];
}
}
}
}
但是效果并不是很好,结果如下图所示,可见变换后的图像虽然比以前增强了,但是几乎变成了灰度图像。
以上是关于直方图均衡化原理与实现的主要内容,如果未能解决你的问题,请参考以下文章
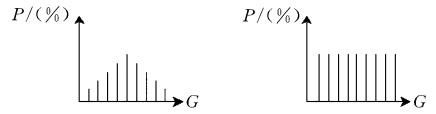


![clip_image002[6] clip_image002[6]](https://image.cha138.com/20210612/f67804e8bd6741f7aa903ea8f8d59828.jpg)
![clip_image004[6] clip_image004[6]](https://image.cha138.com/20210612/03975c2209d1400288877a8e2f55e0b4.jpg)