图像比对的原理或者算法

Posted 2023-04-13

是这样子的，有2张图片，一张是样图，做参考的，一张是摄像头或者相机拍下来的，问题是：在编程语言中用什么方法比对这2张图中哪里不一样？

原理如下：
首先两张图要配准（可以姑且理解为对准），然后做减法就可以得到两张图不同的地方。
题主可以先从图像配准开始学习。

关于编程语言和工具：
在C/C++下的图像处理库OpenCV是很强的的工具，Matlab下用图形处理工具箱也很方便。
总之，题主要学的还有很多，不是那么简单的。 参考技术A 原理如下：
首先两张图要配准（可以姑且理解为对准），然后做减法就可以得到两张图不同的地方。
题主可以先从图像配准开始学习。

关于编程语言和工具：
在C/C++下的图像处理库OpenCV是很强的的工具，Matlab下用图形处理工具箱也很方便。
总之，题主要学的还有很多，不是那么简单的。 参考技术B 有噪声情况下。1、配准；2、两张图的图像块分别计算特征（lbp,sift等）；3、计算特征的距离（欧式距离等）。在matlab或opencv下都可以。

基于开源算法实现图片比对进行图片全图和局部 比对

 

需要最新源码，或技术提问，请加QQ群：538327407，由于源码在不断完善，会在之后同步到AI开源项目中

一、需求 

需要针对艺术品 局部和全图进行相识度比对，从而识别图片的真伪。

 

二、技术思路

通过AI 算法，查找两张图片的相似点，特征点的比对比例分析，如果达到90% 以上，默认相同或者相识。

 

三、技术储备

 

FREAK算法

简介
        FREAK算法是2012年CVPR上《FREAK: Fast Retina Keypoint》文章中，提出来的一种特征提取算法，也是一种二进制的特征描述算子。

        它与BRISK算法非常相似，个人觉得就是在BRISK算法上的改进，关于BRISK算法详见上一篇博文：BRISK特征提取算法。FREAK依然具有尺度不变性、旋转不变性、对噪声的鲁棒性等。

FREAK算法

采样模式
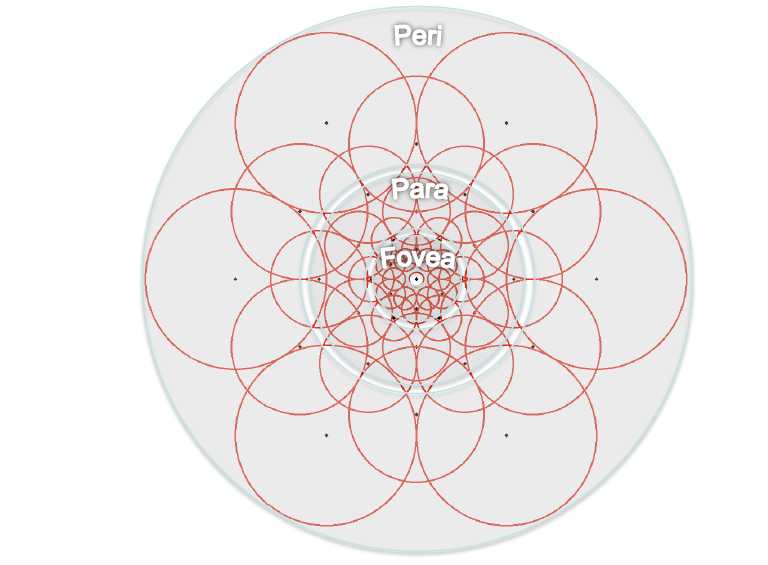
        在BRISK算法中，采样模式是均匀采样模式（在同一圆上等间隔的进行采样）；FREAK算法中，采样模式发生了改变，它采取了更为接近于人眼视网膜接收图像信息的采样模型。图中展示了人眼视网膜拓扑结构，Fovea区域主要是对高进度的图像信息进行处理，Para主要是对低精度的图像信息进行处理。采样点为：6、6、6、6、6、6、6、1，那个1是特征点。

 

表示采样点对Pa中前一个采样点的像素值，同理，表示后一个采样点的像素值。

        当然得到特征点的二进制描述符后，也就算完成了特征提取。但是FREAK还提出，将得到的Nbit二进制描述子进行筛选，希望得到更好的，更具有辨识度的描述子，也就是说要从中去粗取精。（也就是降维）

1、建立矩阵D，D的每一行是一个FREAK二进制描述符，即每一行有N个元素；在上图的采样模式中公有43个采样点，可以产生N=43*(43-1)/2=903个采样点对，也就是说矩阵D有903行列（修改于：2015-11-15）；

2、对矩阵D的每一列计算其均值，由于D中元素都是0/1分布的，均值在0.5附近说明该列具有高的方差；

3、每一列都有一个均值，以均值最接近0.5的排在第一位，均值离0.5越远的排在越靠后，对列进行排序；

4、选取前512列作为最终的二进制描述符。(也可以是256、128、64、32等)

       小结：最原始的二进制长度为903，当然这包含了许多冗余或粗糙的信息，所以根据一定的方法取N个二进制长度，方法是建立矩阵D。假如提取到228个特征点，那么矩阵D应该是228行*903列，然后经过计算均值，将每个列重新排序，选取前N列，这个矩阵D就是228*N的矩阵了。当然这个N我在文中写得是512，你也可以是256、128、64、32这些都是可以的。 最终D的每一行仍然是一个特征点的描述符，只是更短小精悍而已，即降低了维度。（添加于：2016-01-11）

由于FREAK描述符自身的圆形对称采样结构使其具有旋转不变性，采样的位置好半径随着尺度的变化使其具有尺度不变性，对每个采样点进行高斯模糊，也具有一定的抗噪性能，像素点的强度对比生成二进制描述子使其具有光照不变性。因此由上述产生的二进制描述子可以用来进行特征匹配。在匹配之前，再补充一下特征点的方向信息。

特征方向
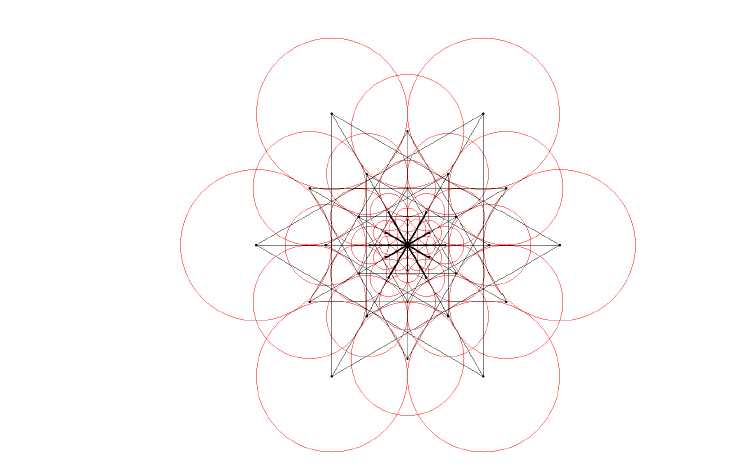
        由于特征点周围有43个采样点，可产生43*(43-1)/2=903个采样点对，FREAK算法选取其中45个长的、对称的采样点对来提取特征点的方向，采样点对如下：

 

 

用O表示局部梯度信息，M表示采样点对个数，G表示采样点对集合，Po表示采样点对的位置，则：

 

 

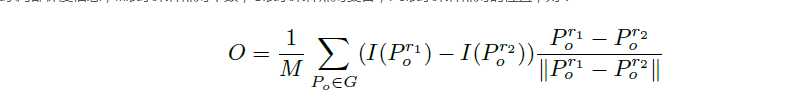
同BRISK算法，可得到特征点的方向。

特征匹配
        在特征描述中，我们得到了512bit的二进制描述符，该描述符的列是高方差——>低方差的排列，而高方差表征了模糊信息，低方差表征了细节信息，与人眼视网膜相似，人眼先处理的是模糊信息，再处理细节信息。因此，选取前128bit即16bytes进行匹配（异或），若两个待匹配的特征点前16bytes距离小于设定的阈值，则再用剩余的位信息进行匹配。这种方法可以剔除掉90%的不相关匹配点。注意：这里的16bytes的选取是建立在并行处理技术（SIMD）上的，并行处理技术处理16bytes与处理1bytes的时间相同；也就是说，16bytes并不是固定的，如果你的并行处理技术能处理32bytes与处理1bytes的时间相同的话，那么你也可以选取前32bytes。

技术实现

 

代码

  public IEnumerable<TFeature>[] Transform(Bitmap[] input)
        {
            return Transform(input, new IList<TFeature>[input.Length]);
        }

        public IEnumerable<TFeature>[] Transform(Bitmap[] input, IEnumerable<TFeature>[] result)
        {
            for (int i = 0; i < input.Length; i++)
                result[i] = Transform(input[i]);
            return result;
        }

 

 private void btnFreak_Click(object sender, EventArgs e)
        {
            if (string.IsNullOrWhiteSpace(label1.Text) || string.IsNullOrWhiteSpace(label2.Text))
            {

                MessageBox.Show("请先上传比对图片！");

                return;
            }

          
            Concatenate concatenate1 = new Concatenate(img1);
            pictureBox.Image = concatenate1.Apply(img2);

         
            FastRetinaKeypointDetector freak = new FastRetinaKeypointDetector();
            //获取两张图片的采样点
            keyPoints1 = freak.Transform(img1);
            keyPoints2 = freak.Transform(img2);

       
            Bitmap img1mark = new PointsMarker(keyPoints1.Select(x => (IFeaturePoint)x).ToList()).Apply(img1);
            Bitmap img2mark = new PointsMarker(keyPoints2.Select(x => (IFeaturePoint)x).ToList()).Apply(img2);

           
            Concatenate concatenate2 = new Concatenate(img1mark);
            pictureBox.Image = concatenate2.Apply(img2mark);
        }

    private void btnCorrelation_Click(object sender, EventArgs e)
        {
            if (keyPoints1 == null)
            {
                MessageBox.Show("Please, click FREAK button first! :-)");
                return;
            }



            Thread t1 = new Thread(new ThreadStart(() =>
            {
                this.Invoke(new Action(() =>
                {
                    lb_result.Text = "检测中......";
                }));

                var matcher = new KNearestNeighborMatching<byte[]>(5, new Hamming());
                IntPoint[][] matches = matcher.Match(keyPoints1, keyPoints2);//返回的结果值一般都是相同的，数组中
                string result1 = (((decimal)matches[0].Count() / (decimal)keyPoints1.Count()) * 100).ToString("#0.00");
                string result2 = (((decimal)matches[1].Count() / (decimal)keyPoints2.Count()) * 100).ToString("#0.00");
                string tempString = string.Format("原图采样点：{0},对比图采样点：{1},匹配个数点：{2},{3},匹配比例：{4}%,{5}%",
                    keyPoints1.Count(), keyPoints2.Count(), matches[0].Count(), matches[1].Count(), result1, result2);

                this.Invoke(new Action(() =>
                {
                    lb_result.Text = tempString;
                    lb_result.BackColor = Color.Azure;
                
                    correlationPoints1 = matches[0];
                    correlationPoints2 = matches[1];

                
                    Concatenate concat = new Concatenate(img1);
                    Bitmap img3 = concat.Apply(img2);

                   
                    PairsMarker pairs = new PairsMarker(
                        correlationPoints1, // Add image1‘s width to the X points to show the markings correctly
                        correlationPoints2.Apply(p => new IntPoint(p.X + img1.Width, p.Y)));

                    pictureBox.Image = pairs.Apply(img3);

                }));

            }));

            t1.Start();

        }

 

  private IntPoint[][] match(IFeaturePoint<T>[] points1, IFeaturePoint<T>[] points2)
        {
            if (points1.Length == 0 || points2.Length == 0)
                throw new ArgumentException("Insufficient number of points to produce a matching.");


            bool swap = false;



            if (points2.Length > points1.Length)
            {
                var aux = points1;
                points1 = points2;
                points2 = aux;
                swap = true;
            }


        
            T[] features1 = new T[points1.Length];
            for (int i = 0; i < features1.Length; i++)
                features1[i] = points1[i].Descriptor;

            T[] features2 = new T[points2.Length];
            for (int i = 0; i < features2.Length; i++)
                features2[i] = points2[i].Descriptor;

            var knn = CreateNeighbors(features1);

            double[] scores = new double[features2.Length];
            int[] labels = new int[features2.Length];
            knn.Score(features2, ref labels, result: scores);

            int[] bestMatch = new int[points1.Length];
            double[] bestScore = new double[points1.Length];
            for (int i = 0; i < bestScore.Length; i++)
                bestScore[i] = Double.PositiveInfinity;

  
            for (int j = 0; j < labels.Length; j++)
            {
                int i = labels[j];

                if (scores[j] > Threshold)
                {
                    if (scores[j] < bestScore[i])
                    {
                        bestScore[i] = scores[j];
                        bestMatch[i] = j;
                    }
                }
            }


            var p1 = new List<IntPoint>(bestScore.Length);
            var p2 = new List<IntPoint>(bestScore.Length);

           
            for (int i = 0; i < bestScore.Length; i++)
            {
                IFeaturePoint<T> pi = points1[i];

                if (bestScore[i] != Double.PositiveInfinity)
                {
                    int j = bestMatch[i];
                    IFeaturePoint<T> pj = points2[j];
                    p1.Add(new IntPoint((int)pi.X, (int)pi.Y));
                    p2.Add(new IntPoint((int)pj.X, (int)pj.Y));
                }
            }

            IntPoint[] m1 = p1.ToArray();
            IntPoint[] m2 = p2.ToArray();

          

            if (swap)
                return new IntPoint[][] { m2, m1 };
            return new IntPoint[][] { m1, m2 };
        }

 

 效果比对

 

 

 

 

 

 

 

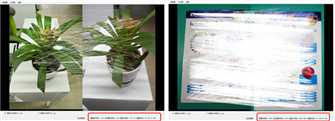
 中国名画

 

 

 结论