自适应滤波：奇异值分解SVD

Posted 2020-09-08 桂。

作者：桂。

时间：2017-04-03  19:41:26

链接：http://www.cnblogs.com/xingshansi/p/6661230.html 

---

【读书笔记10】

前言

广义逆矩阵可以借助SVD进行求解，这在上一篇文章已经分析。本文主要对SVD进行梳理，主要包括：

　　1）特征向量意义；

　　2）特征值分解与SVD；

　　3）PCA与SVD；

内容为自己的学习记录，其中多有借鉴他人之处，最后一并给出链接。

一、特征向量

第一反应是：啥是特征向量？为什么好好的一个矩阵，要拆成这个模样？先看定义

$Av = \\lambda v$

矩阵对应线性变换，可以看到特征向量是这样：线性变换后，只伸缩，既不平移、也不旋转。如计算$A^5v$，可以直接用$\\lambda^5 v$，省去多少计算？

维基百科有一张图很直观：

她的微笑是不是有熟悉的味道o(^▽^)o？不过这里不解读微笑，看红线→：矩阵线性变换后，方向也发生了改变，所以它不是特征向量; 蓝线→：线性变换之后，方向不变，所以是特征向量。由此也可见，特征向量是一个族，而不是独一无二的。

 

二、奇异值分解

　　A-特征值分解（EVD，Eigenvalues Decomposition）

这里分析酉矩阵，假设矩阵$\\bf{B}$具有${\\bf{B}} = {\\bf{A}}{{\\bf{A}}^H}$的形式，根据特征值定义：

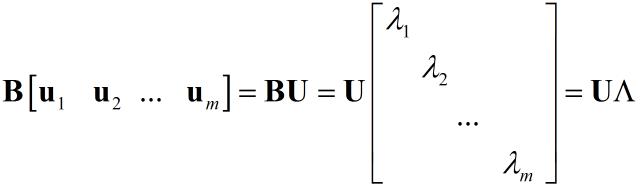
根据酉矩阵特性：

${\\bf{B}} = {\\bf{U}}\\Lambda {{\\bf{U}}^H}$

这里仍然可以写成求和的形式，这也是显然的：酉矩阵张成的空间，就是每一个维度成分的叠加嘛。

　　B-奇异值分解（SVD，Singularly Valuable Decomposition）

根据矩阵变换特性：

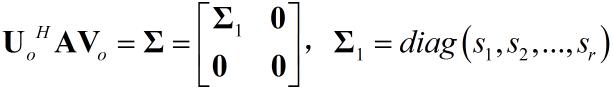
其中$\\bf{A}$是$m$x$n$的矩阵，$\\bf{U_o}$为$m$x$m$，$\\bf{V_o}$为$n$x$n$定义$\\bf{B}$,并借助EVD进行分析：

因为是酉矩阵，从而${{\\bf{U}}_o} = {\\bf{U}}$。${\\bf{\\Sigma }}$为$m$x$n$，且，${s_i} = \\sqrt {{\\lambda _i}}, i=1,2,...min(m,n)$，至此完成$\\bf{U_o}$和${\\bf{\\Sigma }}$的求解，还剩下$\\bf{V_o}$。

对于${\\bf{V_o}}$则有：

${\\bf{AV_o}} = {\\bf{U\\Sigma }}$

即${{\\bf{U}}^H}{\\bf{A}} = {\\bf{\\Sigma }}{{\\bf{V_o}}^H}$，因为有对角阵，转化为向量运算很方便，对于缺失的部分可以借助施密特正交化进行补全。

至此完成SVD分解。

总结SVD思路：

步骤一：利用$AA^H$求解矩阵$U$，并构造$S$;

步骤二：求解$V_o$，并借助施密特正交化构造完整的$V$。

特征值求解、施密特正交化，任何一本线性代数应该都有，所以这里假设特征值分解EVD、施密特正交化直接调用，给出SVD求解的代码（与svd指令等价）：

a = [ 1     7     5
     1     6     4
     2     7     8
    10     5     4]\';
[E,D] = eig(a*a\');
%预处理
[val,pos] = sort(diag(D),\'descend\');
E = E(:,pos);
D = diag(val);
mina = min(size(a));
%SVD分解
U = E; %完成U求解
S = zeros(size(a));
S(1:mina,1:mina) = diag(sqrt(val(1:mina)));%完成S求解
Vo = [U(:,1:mina)\'*a]\'./repmat(diag(S)\',size(a,2),1);%求解Vo
V = [Vo null(Vo\')];%完成V求解，补全正交基，可借助施密特正交化

　　

三、PCA与SVD

根据上文分析，可以看出SVD或者EVD都可以分解出特征值以及特征向量。 

再来回顾以前PCA一文的求解思路：

• 步骤一：数据中心化——去均值，根据需要，有的需要归一化——Normalized；
• 步骤二：求解协方差矩阵；
• 步骤三：利用特征值分解/奇异值分解 求解特征值以及特征向量；
• 步骤四：利用特征向量构造投影矩阵；
• 步骤五：利用投影矩阵，得出降维的数据。

PCA的核心就是根据特征值的大小/总的比例  确定对应特征向量的个数，从而构造投影矩阵。简而言之：有了特征值、特征向量，也就相当于有了PCA。

而EVD/SVD是得到特征值、特征向量的方式，可以说EVD/SVD是PCA的基础，PCA是二者的应用方式。