设无向图G（如图），要求给出改图的深度优先和广度优先遍历的序列，并给出该图的最小生成树

Posted 2023-04-16

谢谢帮忙

参考技术A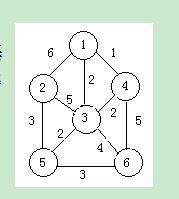

图来啦

参考技术B 深度:125364,广度:123456,最小生成树T的边集为E=(1,4),(1,3),(3,5),(5,6),(5,6) 参考技术C 没图啊 参考技术D 没图。

Java数据结构54:图的深度优先遍历与广度优先遍历数据结构课程设计

54:图的深度优先遍历与广度优先遍历

时间限制: 20000ms 内存限制: 131072kB

描述

给出一个无向图顶点和边的信息，输出这个无向图的深度优先遍历序列和广度优先遍历序列。从一个顶点出发如果有2个以上的顶点可以访问时，我们约定先访问编号大的那个顶点。示例输入对应的图如下图所示：

输入

输入的第1行有2个整数m和n。表示图g有m个顶点和n条边。
第2行是m个以空格隔开的字符串，依次是图中第1个顶点的名字，第2个顶点的名字.....第m个顶点的名字。
此后还有n行，每行由2个字符串构成，分别是构成图中1条边的两个顶点。我们约定不会有重边。

输出

输出有2行。
第1行是从第1个顶点出发对图g做深度优先遍历得到的顶点序列。
第2行是从第1个顶点出发对图g做广度优先遍历得到的顶点序列。

样例输入

8 9
v1 v2 v3 v4 v5 v6 v7 v8
v1 v2
v1 v3
v1 v6
v2 v3
v2 v4
v3 v4
v4 v6
v5 v6
v7 v8

样例输出

v1 v6 v5 v4 v3 v2 v7 v8
v1 v6 v3 v2 v5 v4 v7 v8

提示

注意：从一个顶点出发如果有2个以上的顶点可以访问时，我们约定先访问编号大的那个顶点。

 

 

首先声明，上课没听讲，代码瞎搞的，纯属做着玩，写得质量不好，但是能通过OpenJudge的测试，管他三七二一，反正我过了就行了，好的，废话不多说，直接上代码，拿去就能运行。

import java.util.*;

/**
 * @author baikunlong
 * @date 2020/6/23 10:55
 */
public class Main {
    private static ArrayList<Graph> list = new ArrayList<>();
    private static ArrayList<Graph> visited;

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int m = scanner.nextInt();
        scanner.nextLine();
        String[] names = scanner.nextLine().split(" ");
        for (int i = 0; i < names.length; i++) {
            list.add(new Graph(Integer.parseInt(names[i].substring(1))));
        }
        for (int i = 0; i < m; i++) {
            String[] strings = scanner.nextLine().split(" ");
            Graph graph = list.get(Integer.parseInt(strings[0].substring(1)) - 1);
            graph.list.add(list.get(Integer.parseInt(strings[1].substring(1)) - 1));
            graph = list.get(Integer.parseInt(strings[1].substring(1)) - 1);
            graph.list.add(list.get(Integer.parseInt(strings[0].substring(1)) - 1));
        }

        //开始深度遍历
        visited = new ArrayList<>();
        Graph cGraph = list.get(0);
        visited.add(cGraph);
        DFS(cGraph);
        for (int i = 0; i < visited.size(); i++) {
            System.out.print("v" + visited.get(i).gravity + " ");
        }

        System.out.println();

        //开始广度遍历
        visited = new ArrayList<>();
        //恢复访问状态
        for (int i = 0; i < list.size(); i++) {
            list.get(i).visited = false;
            list.get(i).preGraph = null;
        }
        cGraph = list.get(0);
        visited.add(cGraph);
        ArrayList<Graph> cGraphs = new ArrayList<>();
        cGraphs.add(cGraph);
        BFS(cGraphs);

        for (int i = 0; i < visited.size(); i++) {
            System.out.print("v" + visited.get(i).gravity + " ");
        }
    }

    /**
     * 广度优先遍历
     * @param cGraphs 当前点的连接点集合
     */
    private static void BFS(ArrayList<Graph> cGraphs) {
//        System.out.println("set " + cGraphs);
        //是否还存在没访问的点
        boolean isEmpty = true;
        ArrayList<Graph> nextGraphs = new ArrayList<>();
        //遍历每个连接点
        for (int i = 0; i < cGraphs.size(); i++) {
            Graph cGraph = cGraphs.get(i);
            ArrayList<Graph> cList = cGraph.list;
            if (cList.size() != 0) {
                cList.sort(Comparator.comparingInt(o -> (o.gravity)));
                Collections.reverse(cList);
                //把连接点的所有子连接点给访问了，还是遵循从大大小，上面已排序
                for (int k = 0; k < cList.size(); k++) {
                    Graph graph = cList.get(k);
                    graph.preGraph = cGraph;
                    graph.visited = true;
                    if (!visited.contains(graph)){
                        visited.add(graph);
                        isEmpty = false;
                    }
                    //保存为下一层的连接点
                    nextGraphs.add(graph);
                }
            }
        }
        //如果所有连接点都访问了
        if (isEmpty) {
            //遍历剩下的其他的未连接的点
            for (int i = 0; i < list.size(); i++) {
                if (!list.get(i).visited) {
                    visited.add(list.get(i));
                    cGraphs = new ArrayList<>();
                    cGraphs.add(list.get(i));
                    BFS(cGraphs);
                }
            }
        }else {
            //访问下一层
            BFS(nextGraphs);
        }

    }

    /**
     * 深度优先遍历
     * @param cGraph 当前点
     */
    private static void DFS(Graph cGraph) {
//        System.out.println("set v" + cGraph.gravity);
        //设置被访问
        cGraph.visited = true;
        //如果被访问集合不包含则添加该点
        if (!visited.contains(cGraph))
            visited.add(cGraph);
        ArrayList<Graph> cList = cGraph.list;
        if (cList.size() == 0) {
            //如果该点的连接点为空，代表已到最深处，则回到上一个点
            DFS(cGraph.preGraph);
            return;
        }
        //根据权重排序，优先访问大的点
        cList.sort(Comparator.comparingInt(o -> (o.gravity)));
        Collections.reverse(cList);
//        System.out.println(cList);

        //访问每一个连接点
        for (int i = 0; i < cList.size(); i++) {
            if (!cList.get(i).visited) {
                cList.get(i).preGraph = cGraph;
                cGraph = cList.get(i);
                //递归访问下去，知道没有连接点为止
                DFS(cGraph);
                return;
            }
        }
        //如果没有回到起点则继续遍历
        if (cGraph.preGraph != null) {
            DFS(cGraph.preGraph);
        } else {
            //遍历剩下的未连接的点
            for (int i = 0; i < list.size(); i++) {
                if (!list.get(i).visited) {
                    DFS(list.get(i));
                }
            }
        }
    }

    static class Graph {
        //权重
        int gravity;
        //连接点
        ArrayList<Graph> list = new ArrayList<>();
        //是否访问
        boolean visited;
        //上一个点
        Graph preGraph;

        public Graph(int gravity) {
            this.gravity = gravity;
        }

        @Override
        public String toString() {
            return "Graph{" +
                    "gravity=" + gravity +
                    ‘}‘;
        }
    }
}

 推荐：全球市场营销推广专家，全球7位营销大师

金卡有什么用，金卡具备哪些特殊权益

重庆网站建设推广服务，网站建设中的几种推广方法