OpenGL光栅化作业:bresenham算法GL_POINTS为基础画线段
Posted 荒废的养鸡场
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了OpenGL光栅化作业:bresenham算法GL_POINTS为基础画线段相关的知识,希望对你有一定的参考价值。
首先来看一下题目要求:
2.2 Draw a Line
Implement your line rasterization algorithm in OpenGL. You can only use integer arithmetic in your code.
- Input: 2 2D points, that makes 4 integers, as a start point and an end point
- Output: A straight line in a window
- You can only use the
GL_POINTSas primitives. Other (i.e.GL_LINESorGL_LINE_STRIP) primitives is not allowed to use.
-
Language: Only C/C++ is accepted in this homework.
-
Libraries: OpenGL and freeGLUT/GLFW
-
IDE: Any IDE can be used.
这里我的的开发环境是mac OS Sierra 10.2.3,使用Sublime做C++语言编写,直接在terminal使用g++编译。使用的library是GLFW,由于编译时需要链接的库文件还是蛮多的,这里也可以用Xcode配置好环境再编写,或者直接用makefile。这个环境配置的问题就下次再说了(其实也不知道下次会拖到什么时候)。
首先来审题,要求只用GL_POINTS做primitives,那么从几何数学的角度来看就是用连续的无数个点来集成一条线段。而且考察的是bresenham的光栅化算法,也就是把连续图形转换为计算机可以显示离散的像素点的一种做法,那么题意应该是要将我们理想中的一条【连续】的线段,【光栅化】处理后变成一系列有限的【离散】的点的集合,这些点的数量足够大,相隔间隙足够小,使得在计算机屏幕显示时在视觉上形成一条【看似连续】的线段。
然后来谈谈在审完题之后思考的一些问题。
第一,要求我们输入的是两个整数对(代表线段两个端点的坐标),但OpenGL的默认显示坐标范围是[-1,1]区间内的浮点数,而bresenham算法所做的是将连续的线段变为离散的点的坐标(坐标值也为整数对)。所以输入和输出到底要作些什么转化?
输入的是两个整数对,我们在数学上可以通过计算出直线的表达式,知道直线上的无数个点的X、Y坐标的范围,以及它们所遵循的一种关系。光栅化所做的就是对这些点进行一个采样量化的操作,在这连续的无数多个点中适当地采样出足够的点的值(比如在横坐标上进行整数采样),再对另一项坐标值进行量化(比如Y坐标量化得到的值也都是整数)。然后再将我们光栅化后得到的有限的一系列的点(坐标值为整数),将它们的坐标值规格化到[-1,1]。得到合适的浮点数,用OpenGL进行绘制。
规格化这方面就写了个normalize()函数,输入-500到500之间的整数,返回-1到1之间的浮点数。
想好了步骤就分部地研究这些问题。
首先确定好输入的范围,不确定好输入范围的话用户也不知道你画出的线段是不是他需要的大小比例。由于我们要使屏幕上展示的点的数量足够多以在视觉上形成连续的线段的效果,所以设定的整数范围应该要比较大,我这里默认设置的输入范围是[-500,500]之间的整数,当然如果要实现更加逼近视觉上连续的效果的话,可以设置更大的输入范围,依次类推。 此外,有朋友跟我交流的一种想法是以用户输入整数中的最大绝对值为输入边界,我想了一下,这样线段的形状当然是用户想要的形状,大小的话线段肯定有一端处在窗口的边界上,这么做是不是要涉及到什么动态的设置我就不清楚了,因为我写的不是这个想法(……)。
然后不管其他,先只考虑位于线段所在直线经过第一象限与x轴夹角小于45度,也就是0<m<1的情况。bresenham算法推导过程不再赘述,直接上结论。因为m=0或者1时画出来的线段也是差不多的,就直接算作0<=m<=1的情况了。

插播一下一下在OpenGL中怎么实现画多个点连成线。我的想法是用分别用两个长度相等的浮点数数组fxarray[]和fyarray[]存储规格化后的xi和yi的值,(其实对就是在光栅化计算出的两个整数数组做一下规格化运算得到的),然后在绘制点的时候循环调用。
for(int i=0;i<length;i++) { glVertex2f(xarray[i],yarray[i]); }
因为在这种情况下,我们选择在x方向上采样,并在y方向上量化。x0到x1之间每个xi的值是固定的,xi=x0+i,而bresenham算法是根据以上过程递推出yi的值。所以我用一个整数数组array[]存储y0到y1之间每个yi的值,array[0]和array[n-1]分别最初赋值y0和y1的值,n为从x0到x1之间的距离。输入dx,dy,和p,array[]的地址及长度到一个递推函数。最初传入的p为p0=2dy-dx,递推结束后数组array就存储了计算出的y0到yn之间的值。
void bresenham(int array[], int p, int i, int length, int dx, int dy) { if(i==length-1) return; int pnext; if(p<=0) { array[i+1]=array[i]; pnext=p+2*dy; } else { array[i+1]=array[i]+1; pnext=p+2*dy-2*dx; } bresenham(array,pnext,i+1,length,dx, dy); }
然后就是考虑其他几种情况的问题了。
(1)m不存在(线段与y轴平行或重合)
(2)-1<=m<0
(3)m>1
(4)m<-1。
情况(1)比较简单,xarray[]中的值一直不变,存储y的数列直接从最低点一直递增最高点。(这里默认y0<=y1,同样在|m|<1的情况下默认x0<x1,|m|>1的情况下默认y0<y1,方便分析。控制这个在前面写个条件判断的交换函数也很容易。)
if(x0==x1) { if(y0>y1) { int tempy=y0; y0=y1; y1=tempy; } length=y1-y0+1; for(int i=0;i<length;i++) { xarray[i]=x0; yarray[i]=y0+i; }
因为数学差(……)不想做其他情况的bresenham算法推导,所以直接采用了对称变换的思想。直接改变传入bresenham()中的参数并作一些相应的变换来求结果。没有去网上参考其他人是什么样的做法,也不知道这种对称变换+数组记录的方式会不会更复杂了吧(……)。
情况(2)其实和最开始讨论的0<=m<=1完全关于y轴对称,只需要先把既定的y0和y1的值关于y轴做一下轴对称变换(也就是*-1),用bresenham计算出来的yarray[]一定与我们要求的yarray[]关于y轴对称,再*-1即可求得。当然,由于y的值做了变换,所以传入bresenham算法中的与y有关的参数也有了相应的改变。以下是|m|<=1时的两种情况的计算方式。
if(fabs(m)<=1) { length=x1-x0+1; for(int i=0;i<length;i++) xarray[i]=x0+i; //0<m<=1 if(dy>=0) { yarray[0]=y0; yarray[length-1]=y1; int p0=2*dy-dx; bresenham(yarray,p0, 0, length,dx,dy); } else { //-1<=m<0 yarray[0]=-y0; yarray[length-1]=-y1; int p0=2*(-dy)-dx; bresenham(yarray,p0,0,length,dx,-dy); for(int i=0;i<length;i++) yarray[i]=-yarray[i]; }
然后到了情况(3)和(4)。先考虑情况(3)。情况(4)与上同理,只需要做一个关于y轴的轴对称变换。
由于|m|>1,y轴上的变化尺度要比x轴上的大,所以应该在y轴上取样,在x轴上量化。这里相当于是把水平直角坐标系逆时针方向旋转了90度来思考问题,m>1的情况与y轴正方向的夹角为0~45度,就相当于最初讨论的最基本0<=m<=1的情况。length改为从y0到y1的距离,向bresenham算法中传入的数组也变为了xarray[],传入参数变成了p0=2*dx-dy。这个旋转坐标系的想法吧说难也不难,不过刚开始想的时候翻车了挺多次的(……),想明白了就好。底下是|m|>1的情况(3)(4)。
} else { length=y1-y0+1; for(int i=0;i<length;i++) yarray[i]=y0+i; if(dx>=0) { //m>1 xarray[0]=x0; xarray[length-1]=x1; int p0=2*dx-dy; bresenham(xarray,p0,0,length,dy,dx); } else { //m<-1 xarray[0]=-x0; xarray[length-1]=-x1; int p0 = 2*(-dx)-dy; bresenham(xarray,p0,0,length,dy,-dx); for(int i=0;i<length;i++) xarray[i]=-xarray[i]; }
然后在进行对输入(x0,y0), (y0, y1)的处理就是在进行bresenham算法处理之前,保证当|m|<=1时,x0<=x1,|m|>1时,y0<=y1,|m|不存在时,y0<=y1。这里就不详细解释了。直接看完全代码。
1 #include <iostream> 2 #include <math.h> 3 #include <GLFW/glfw3.h> 4 using namespace std; 5 //g++ -o line line.cpp -lglfw3 -framework Cocoa -framework OpenGL -framework IOKit -framework CoreVideo 6 void show(float xarray[],float yarray[],int length) { 7 bool init = true; 8 if(!glfwInit()) { 9 cout << "Initialization failed" << endl; 10 init = false; 11 //return? 12 } 13 14 //create a window with its OpenGL context 15 GLFWwindow* window1 = glfwCreateWindow(640, 640, "line", NULL, NULL); 16 17 if (!window1) { 18 cout << "Window or OpenGL context creation failed" << endl; 19 glfwTerminate(); 20 //return? 21 } 22 if(init&&window1) { 23 // Make the window\'s context current */ 24 glfwMakeContextCurrent(window1); 25 26 while (!glfwWindowShouldClose(window1)) { 27 // Keep running 28 /* Draw a triangle */ 29 glBegin(GL_POINTS); 30 31 glColor3f(1, 0.52, 0.0); // Orange 32 for(int i=0;i<length;i++) { 33 glVertex2f(xarray[i],yarray[i]); 34 } 35 36 glEnd(); 37 38 //When the frame is rendered, swap the buffer with one another 39 glfwSwapBuffers(window1); 40 41 /* Poll for and process events */ 42 glfwPollEvents(); 43 } 44 45 if(glfwWindowShouldClose(window1)) 46 glfwDestroyWindow(window1); 47 48 //done before exit 49 glfwTerminate(); 50 } 51 } 52 53 54 float normalize(int input) { 55 return float(input)/500; 56 } 57 void bresenham(int array[], int p, int i, int length, int dx, int dy) { 58 if(i==length-1) 59 return; 60 int pnext; 61 if(p<=0) { 62 array[i+1]=array[i]; 63 pnext=p+2*dy; 64 } 65 else { 66 array[i+1]=array[i]+1; 67 pnext=p+2*dy-2*dx; 68 } 69 bresenham(array,pnext,i+1,length,dx, dy); 70 } 71 72 int main() { 73 int x0, x1, y0, y1; 74 cout << "Please gives the x and y value of two points" << endl; 75 cout << "with one space between them (like: \'x y\')" << endl; 76 cout << "Notice: the x and y value should be integers between -500 and 500" << endl << endl; 77 78 cout << "the x and y value of the first point?" << endl; 79 cin >> x0 >> y0; 80 cout << "the coordinate of the first point: (" << x0 << ", " << y0 <<")." << endl; 81 82 cout << "the x and y value of the second point?" << endl; 83 cin >> x1 >> y1; 84 cout << "the coordinate of the second point: (" << x1 << ", " << y1 <<")." << endl; 85 86 int length; 87 int xarray[1001], yarray[1001]; 88 int dx; 89 int dy; 90 91 if(x0==x1) { 92 if(y0>y1) { 93 int tempy=y0; 94 y0=y1; 95 y1=tempy; 96 } 97 length=y1-y0+1; 98 for(int i=0;i<length;i++) { 99 xarray[i]=x0; 100 yarray[i]=y0+i; 101 } 102 } else { 103 //|m|<=1,let point 1 be on the right of point 0 104 float m=float(y1-y0)/float(x1-x0); 105 if(fabs(m)<=1&&x0>x1) { 106 int tempx=x0; 107 int tempy=y0; 108 x0=x1; 109 y0=y1; 110 x1=tempx; 111 y1=tempy; 112 } 113 //|m|>1, let point 1 be on the top of point 0 114 if(fabs(m)>1&&y0>y1) { 115 int tempy=y0; 116 int tempx=x0; 117 y0=y1; 118 x0=x1; 119 y1=tempy; 120 x1=tempx; 121 } 122 dx=x1-x0; 123 dy=y1-y0; 124 m=float(dy)/float(dx); 125 126 if(fabs(m)<=1) { 127 length=x1-x0+1; 128 for(int i=0;i<length;i++) 129 xarray[i]=x0+i; 130 //0<m<=1 131 if(dy>=0) { 132 yarray[0]=y0; 133 yarray[length-1]=y1; 134 int p0=2*dy-dx; 135 bresenham(yarray,p0, 0, length,dx,dy); 136 } else { 137 //-1<=m<0 138 yarray[0]=-y0; 139 yarray[length-1]=-y1; 140 int p0=2*(-dy)-dx; 141 bresenham(yarray,p0,0,length,dx,-dy); 142 for(int i=0;i<length;i++) 143 yarray[i]=-yarray[i]; 144 } 145 } else { 146 length=y1-y0+1; 147 for(int i=0;i<length;i++) 148 yarray[i]=y0+i; 149 if(dx>=0) { 150 //m>1 151 xarray[0]=x0; 152 xarray[length-1]=x1; 153 int p0=2*dx-dy; 154 bresenham(xarray,p0,0,length,dy,dx); 155 } else { 156 //m<-1 157 xarray[0]=-x0; 158 xarray[length-1]=-x1; 159 int p0 = 2*(-dx)-dy; 160 bresenham(xarray,p0,0,length,dy,-dx); 161 for(int i=0;i<length;i++) 162 xarray[i]=-xarray[i]; 163 } 164 } 165 } 166 167 float fxarray[1001]; 168 float fyarray[1001]; 169 for(int i=0;i<length;i++) { 170 fxarray[i]=normalize(xarray[i]); 171 fyarray[i]=normalize(yarray[i]); 172 } 173 174 show(fxarray,fyarray,length); 175 176 177 178 return 0; 179 }
结果展示
m不存在的情况


m=0的情况


0<m<=1

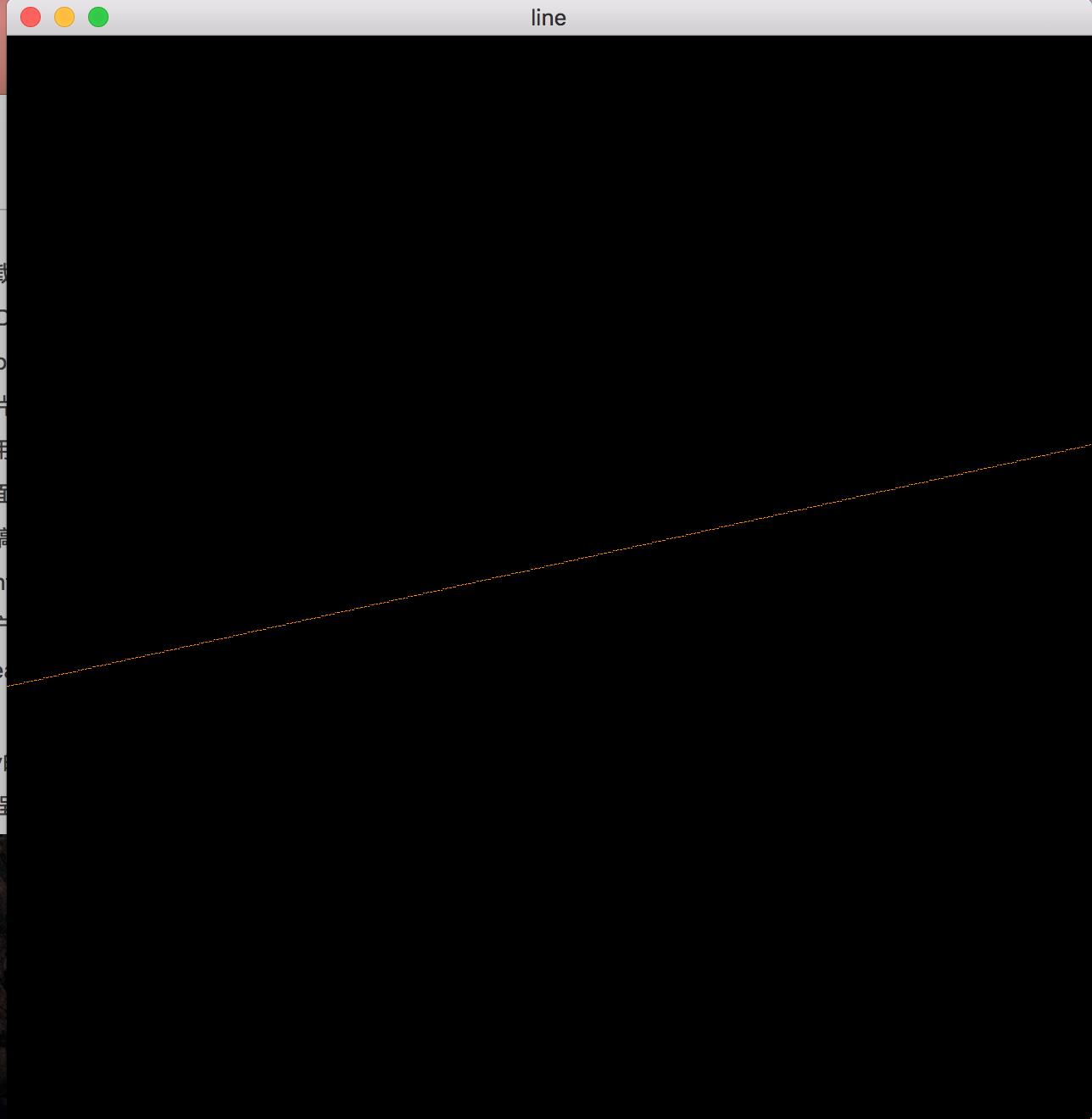
-1<=m<0


m>1
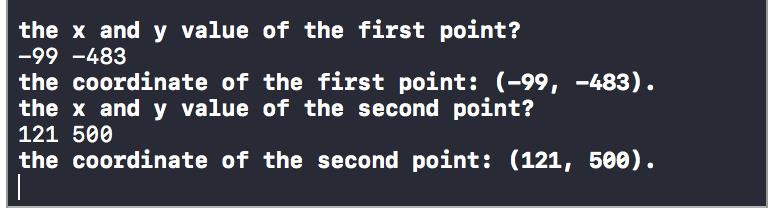
m<-1

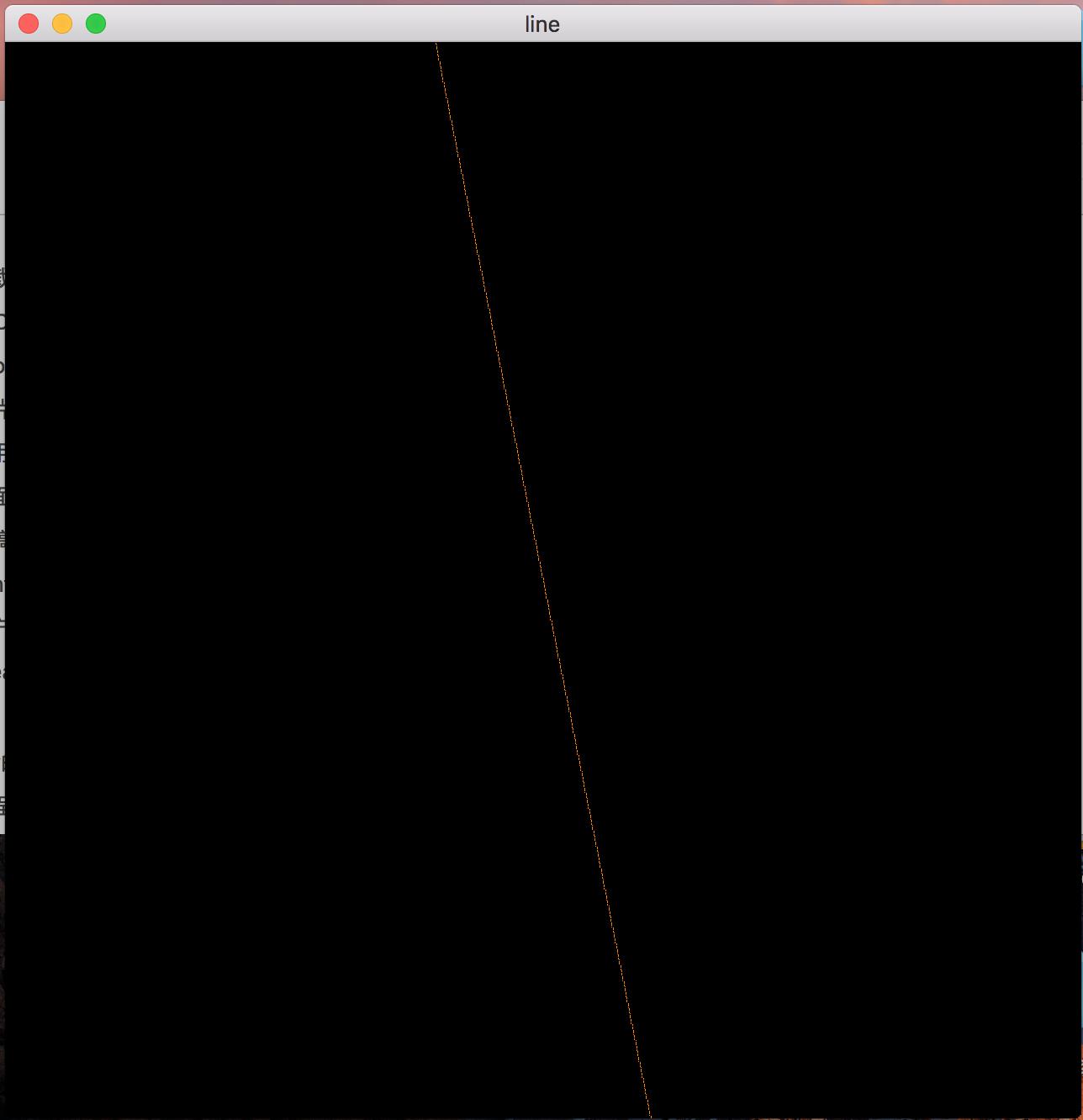
以上是关于OpenGL光栅化作业:bresenham算法GL_POINTS为基础画线段的主要内容,如果未能解决你的问题,请参考以下文章