(转)机器学习之SVD分解
Posted 7岁
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了(转)机器学习之SVD分解相关的知识，希望对你有一定的参考价值。
一、SVD奇异值分解的定义
假设是一个
的矩阵，如果存在一个分解：
其中为
的酉矩阵，
为
的半正定对角矩阵，
为
的共轭转置矩阵，且为
的酉矩阵。这样的分解称为
的奇异值分解，
对角线上的元素称为奇异值，
称为左奇异矩阵，
称为右奇异矩阵。
二、SVD奇异值分解与特征值分解的关系
特征值分解与SVD奇异值分解的目的都是提取一个矩阵最重要的特征。然而，特征值分解只适用于方阵，而SVD奇异值分解适用于任意的矩阵，不一定是方阵。
这里，和
是方阵，
和
为单位矩阵，
为
的特征向量，
为
的特征向量。
和
的特征值为
的奇异值的平方。
三、SVD奇异值分解的作用和意义
奇异值分解最大的作用就是数据的降维，当然，还有其他很多的作用，这里主要讨论数据的降维，对于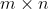
的矩阵
，进行奇异值分解
取其前
个非零奇异值，可以还原原来的矩阵，即前个非零奇异值对应的奇异向量代表了矩阵的主要特征。可以表示为
以上是关于(转)机器学习之SVD分解的主要内容，如果未能解决你的问题，请参考以下文章