数学推导+纯Python实现机器学习算法28：奇异值分解SVD

Posted 2021-04-06 机器学习实验室

Python机器学习算法实现

Author：louwill

Machine Learning Lab

     

     奇异值分解（Singular Value Decomposition，SVD）作为一种常用的矩阵分解和数据降维方法，在机器学习中也得到了广泛的应用，比如自然语言处理中的SVD词向量和潜在语义索引，推荐系统中的特征分解，SVD用于PCA降维以及图像去噪与压缩等。作为一个基础算法，我们有必要将其单独拎出来在机器学习系列中进行详述。

特征值与特征向量

     在学习SVD原理之前，我们有必要对矩阵的特征值与特征向量进行回顾。矩阵的特征值与特征向量定义如下：

     其中 为 矩阵， 为一 维向量，则 定义为矩阵 的一个特征值， 向量是矩阵 的特征值 所对应的特征向量。
     实际计算时，我们通过求解齐次方程 来计算矩阵 的特征值和特征向量。
     将矩阵计算出特征值和特征向量的直接好处就是我们可以将矩阵进行分解，假设矩阵有 个特征值 ，以及每个特征值对应的特征向量 ，那么矩阵 就可以用下式进行分解：

     在线性代数中，我们也将上式成为矩阵的对角化，或者求矩阵的相似矩阵。一般我们会将矩阵 的 个特征向量进行标准化和正交化处理， 满足 ，所以就有 ，即 为酉矩阵。最终上述分解表达式可表示为：

     矩阵要计算特征值和特征向量的一个必要条件就是该矩阵必须要为方阵，即矩阵维度为 。
     但大多数情况下，我们碰到的矩阵都是非方阵的 的情形。当矩阵行列不等时，如果我们也想对其进行矩阵分解，那就必须使用SVD了。

SVD详解

     假设现在我们要对 非方阵 进行矩阵分解，定义分解表达式为：

     其中 为 矩阵， 为 对角阵， 为 矩阵。 和 均为酉矩阵，即 和 满足：

     SVD的图解示意如下图所示。

     我们可以通过求解齐次方程的形式来求解特征值和特征矩阵，那么在上式中，我们如何求解 这三个矩阵呢？

     还是需要借助于矩阵的特征值和特征向量。
     由于矩阵 是非方阵，现在将矩阵 与其转置矩阵做矩阵乘法运算，可得到 的方阵 ，然后对该矩阵求特征值和特征向量：

     由上式我们即可求得方阵 的 个特征值和特征向量，该 个特征向量构成的特征矩阵即为矩阵 。我们把矩阵 中的每个向量称为矩阵 的左奇异向量。
     同理，将矩阵 的其转置矩阵与矩阵 做矩阵乘法运算，同样可得 的方阵 ，然后对该矩阵求特征值和特征向量：

     由上式我们即可求得方阵 的 个特征值和特征向量，该 个特征向量构成的特征矩阵即为矩阵 。我们把矩阵 中的每个向量称为矩阵 的右奇异向量。
     左奇异矩阵 和右奇异矩阵 求出来后，我们只剩下中间的奇异值矩阵 尚未求出。奇异值矩阵 除了对角线上的奇异值，其余元素均为0，所以我们只要求出矩阵 的奇异值即可。可推导：

     所以我们可由上述推导计算得到奇异值矩阵。实际上，由下述推导：

     可知特征值矩阵为奇异值矩阵的平方，即特征值为奇异值的平方。

Python SVD实现

     Python中numpy和scipy两个科学计算库都直接提供了SVD的实现方式，所以我们这里就不再基于numpy手写SVD的实现过程了。下面基于numpy.linalg线性代数模块下的svd函数来看一个计算实例。

import numpy as np# 创建一个矩阵AA = np.array([[0,1],[1,1],[1,0]])# 对其进行SVD分解u, s, vt = np.linalg.svd(A, full_matrices=True)print(u.shape, s.shape, vt.shape)

(3, 3) (2,) (2, 2)

     然后分别查看u、s和v矩阵，并验证下是否可由这三个矩阵恢复到矩阵A。

# 矩阵uprint(u, s, v.T)

array([[-4.08248290e-01, 7.07106781e-01, 5.77350269e-01], [-8.16496581e-01, 5.55111512e-17, -5.77350269e-01], [-4.08248290e-01, -7.07106781e-01, 5.77350269e-01]])array([1.73205081, 1. ])array([[-0.70710678, -0.70710678],       [-0.70710678,  0.70710678]])

     可以看到该svd函数对结果中的奇异值矩阵进行简化了，只给出了奇异值向量，将矩阵中其余为0的元素均省去了。

# 由u,s,v恢复矩阵Anp.dot(u[:,:2]*s, vt)

array([[ 1.11022302e-16, 1.00000000e+00],[ 1.00000000e+00, 1.00000000e+00],[ 1.00000000e+00, -3.33066907e-16]])

     基本能够恢复矩阵A，因浮点数存在计算误差，这里可以忽略不计。

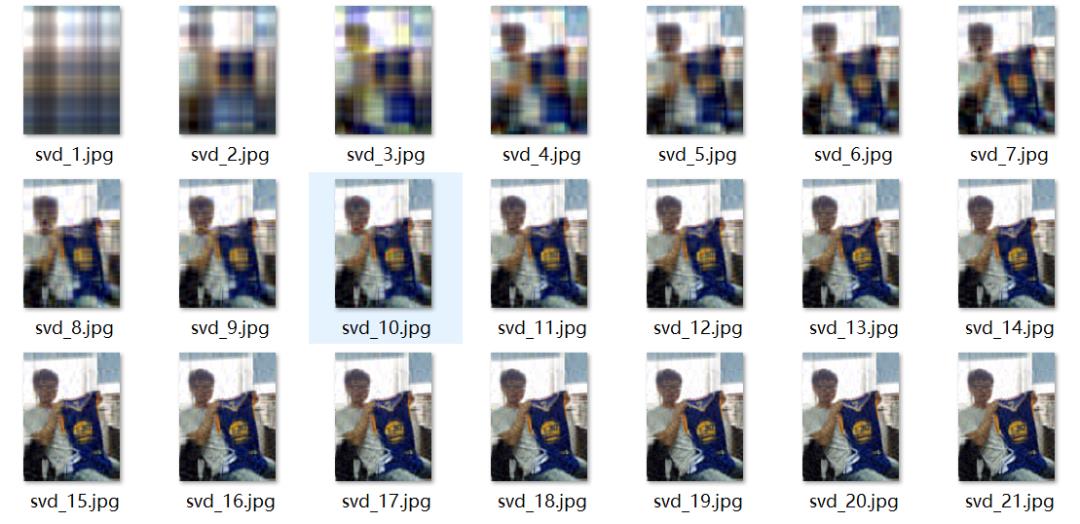
SVD图像压缩

      我们可以尝试将SVD用于图像的压缩算法。其原理就是保存像素矩阵的前k个奇异值，并在此基础上做图像恢复。由SVD的原理我们可以知道，在SVD分解中越靠前的奇异值越重要，代表的信息含量越大。

     下面我们尝试对一个图像进行SVD分解，并分别取前1~50个奇异值来恢复该图像。需要恢复的图像如下（厚着脸皮拿笔者自己作为示例）：

     实现代码如下：

import numpy as npimport osfrom PIL import Imagefrom tqdm import tqdm# 定义恢复函数，由分解后的矩阵恢复到原矩阵def restore(u, s, v, K): ''' u:左奇异矩阵 v:右奇异矩阵 s:奇异值矩阵 K:奇异值个数 ''' m, n = len(u), len(v[0]) a = np.zeros((m, n))for k in range(K): uk = u[:, k].reshape(m, 1) vk = v[k].reshape(1, n)# 前k个奇异值的加总 a += s[k] * np.dot(uk, vk)  a = a.clip(0, 255)return np.rint(a).astype('uint8')A = np.array(Image.open("./ml_lab.jpg", 'r'))# 对RGB图像进行奇异值分解u_r, s_r, v_r = np.linalg.svd(A[:, :, 0]) u_g, s_g, v_g = np.linalg.svd(A[:, :, 1])u_b, s_b, v_b = np.linalg.svd(A[:, :, 2])# 使用前50个奇异值K = 50 output_path = r'./svd_pic'# 恢复图像for k in tqdm(range(1, K+1)): R = restore(u_r, s_r, v_r, k) G = restore(u_g, s_g, v_g, k) B = restore(u_b, s_b, v_b, k) I = np.stack((R, G, B), axis=2)     Image.fromarray(I).save('%s\svd_%d.jpg' % (output_path, k))

     当仅使用一个奇异值时，被压缩后的图像模糊一团，除了颜色线条啥也看不出：

     当使用前10个奇异值时，恢复后的压缩图像隐约可见轮廓，就像打了马赛克一样：

     如此继续扩大奇异值的数量，当我们取到前50个奇异值的时候，恢复后的压缩图像已经相对清晰许多了：

     渐进效果如下：

     总体而言就是图像清晰度随着奇异值数量增多而变好。当奇异值k不断增大时，恢复后的图像就会无限逼近于真实图像。这便是基于SVD的图像压缩原理。

往期精彩：

---

一个算法工程师的成长之路

长按二维码.关注机器学习实验室

  
    
    
  

   
     
     
   
喜欢您就点个在看！