一些数学基础(辗转相除法筛法快速幂)

Posted 2020-08-31

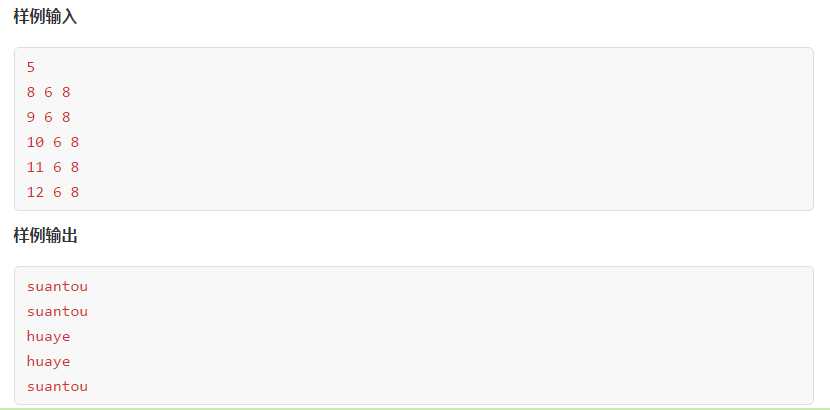
看个题目

 1 #include<iostream>
 2 using namespace std;
 3 int gcd(int a,int b)
 4 {
 5     if(b==0)
 6     {
 7         return a;
 8     }
 9     else
10     {
11         return gcd(b,a%b);
12     }
13 }
14 int main()
15 {
16     int t;
17     cin>>t;
18     while(t--)
19     {
20         int n,a,b;
21         cin>>n>>a>>b;
22         //j,k  j>k
23         //j+k,j-k
24         //j+k+j,j+k+k,j+k+j-k
25         //即每个数都能用mj+nk表示
26         //mj+nk=xgcd(j,k);
27         int s=gcd(a,b);
28         int num=n/s;
29         if(num%2==1)
30         {
31             cout<<"huaye"<<endl;
32         }
33         else
34         {
35             cout<<"suantou"<<endl;
36         }
37     }
38     return 0;
39 }

View Code

最后能取出的石子的编号必然是 gcd(a,b) 的倍数的编号

 

筛法算质数

 

二分快速幂（循环写法）

 

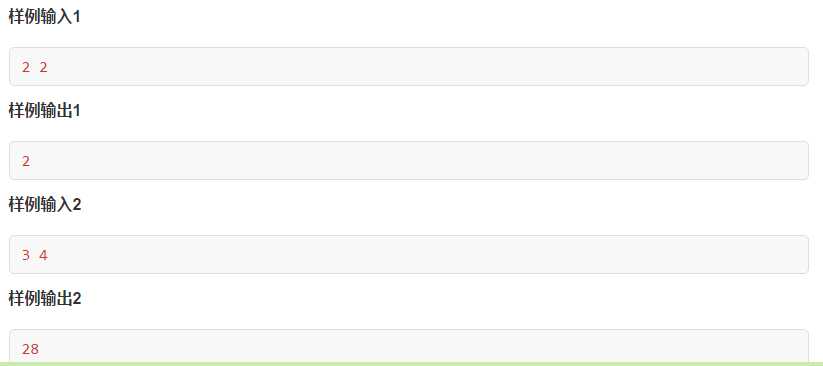
简单题

 1 #include<iostream>
 2 using namespace std;
 3 #define NUM 1000000007
 4 long long pow_mod(long long a,long long b,long long mod)
 5 {
 6     long long res=1,temp=a;
 7     for(;b;b/=2)
 8     {
 9         if(b&1)
10         {
11             res=res*temp%mod;
12         }
13         temp=temp*temp%mod;
14     }
15     return res;
16 }
17 int main()
18 {
19     ios::sync_with_stdio(false);
20     long long n,m;
21     cin>>n>>m;
22     //所求为(pow(m,n)-m*pow(m-1,n-1)) mod NUM
23     long long result=pow_mod(m,n,NUM)-m*pow_mod(m-1,n-1,NUM)%NUM;
24     if(result>=0)
25     {
26         cout<<result<<endl;
27     }
28     else
29     {
30         cout<<NUM+result<<endl;
31     }
32     return 0;
33 }

View Code

 

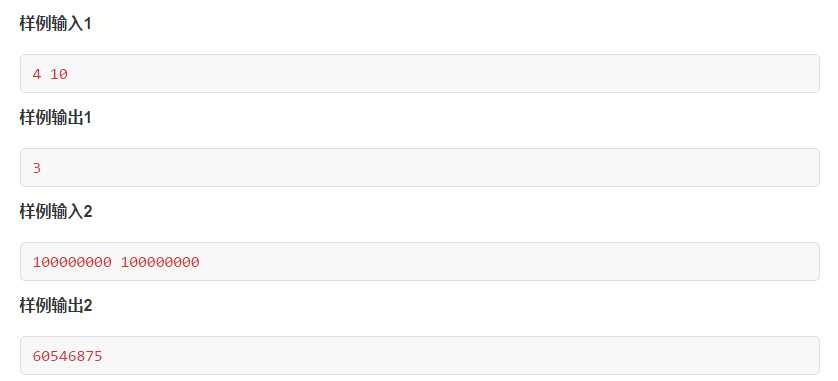
矩阵快速幂

和二分快速幂类似，只是把1换成单位矩阵，乘法换成矩阵乘法

 1 #include<iostream>
 2 using namespace std;
 3 long long n,m;
 4 long long t=2;
 5 struct matrix
 6 {
 7     long long a[50][50];
 8 };
 9 matrix matrix_mul(matrix A,matrix B,long long mod)
10 {
11     matrix C;
12     for(int i=0;i<t;i++)
13     {
14         for(int j=0;j<t;j++)
15         {
16             C.a[i][j]=0;
17             for(int k=0;k<t;k++)
18             {
19                 C.a[i][j]+=A.a[i][k]*B.a[k][j]%mod;
20                 C.a[i][j]%=mod;
21             }
22         }
23     }
24     return C;
25 }
26 matrix unit()
27 {
28     matrix res;
29     for(int i=0;i<t;i++)
30     {
31         for(int j=0;j<t;j++)
32         {
33             if(i==j)
34             {
35                 res.a[i][j]=1;
36             }
37             else
38             {
39                 res.a[i][j]=0;
40             }
41         }
42     }
43     return res;
44 }
45 matrix matrix_pow(matrix A,long long n,long long mod)
46 {
47     matrix res=unit();
48     matrix temp=A;
49     for(;n;n/=2)
50     {
51         if(n&1)
52         {
53             res=matrix_mul(res,temp,mod);
54         }
55         temp=matrix_mul(temp,temp,mod);
56     }
57     return res;
58 }
59 int main()
60 {
61     cin>>n>>m;
62     matrix ma;
63     ma.a[0][0]=ma.a[0][1]=ma.a[1][0]=1;
64     ma.a[1][1]=0;
65     matrix res=matrix_pow(ma,n-2,m);
66     if(n>2)
67     {
68         cout<<(res.a[0][0]+res.a[0][1])%m<<endl;
69     }
70     else
71     {
72         cout<<1%m<<endl;
73     }
74     return 0;
75 }

View Code

 

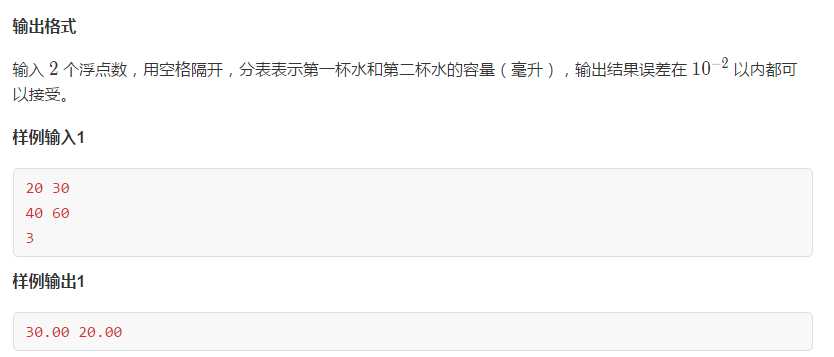
关键是要找到转移矩阵

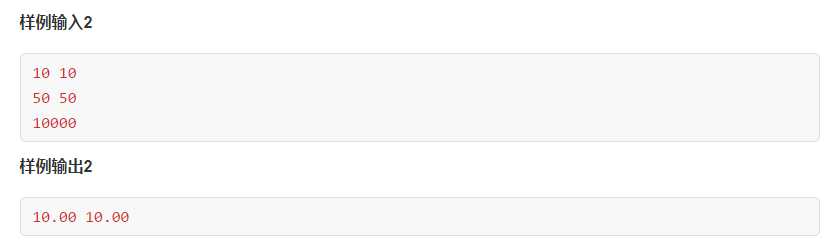
 1 #include<iostream>
 2 #include<stdio.h>
 3 using namespace std;
 4 #define MAXX 10000005
 5 long long n=2;
 6 struct matrix
 7 {
 8     double a[5][5];
 9 };
10 matrix unit()
11 {
12     matrix res;
13     for(int i=0;i<n;i++)
14     {
15         for(int j=0;j<n;j++)
16         {
17             if(i==j)
18             {
19                 res.a[i][j]=1;
20             }
21             else
22             {
23                 res.a[i][j]=0;
24             }
25         }
26     }
27     return res;
28 }
29 matrix matrix_mul(matrix A,matrix B)
30 {
31     matrix C;
32     for(int i=0;i<n;i++)
33     {
34         for(int j=0;j<n;j++)
35         {
36             C.a[i][j]=0;
37             for(int k=0;k<n;k++)
38             {
39                 C.a[i][j]+=A.a[i][k]*B.a[k][j];
40             }
41         }
42     }
43     return C;
44 }
45 matrix matrix_pow(matrix A,long long nn)
46 {
47     matrix res=unit();
48     matrix temp=A;
49     for(;nn;nn/=2)
50     {
51         if(nn&1)
52         {
53             res=matrix_mul(res,temp);
54         }
55         temp=matrix_mul(temp,temp);
56     }
57     return res;
58 }
59 int main()
60 {
61     long long a,b,k;
62     double x,y;
63     cin>>a>>b>>x>>y>>k;
64     //转移矩阵
65     matrix origin;
66     origin.a[0][0]=1-x/100;
67     origin.a[0][1]=y/100;
68     origin.a[1][0]=x/100;
69     origin.a[1][1]=1-y/100;
70     //矩阵的快速幂
71     matrix res=matrix_pow(origin,k);
72 
73     double res_a=res.a[0][0]*a+res.a[0][1]*b;
74     double res_b=res.a[1][0]*a+res.a[1][1]*b;
75     printf("%.9lf %.9lf\\n",res_a,res_b);
76     return 0;
77 }

View Code

 

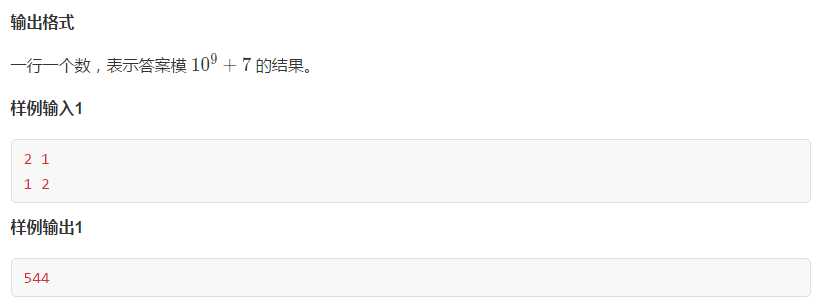
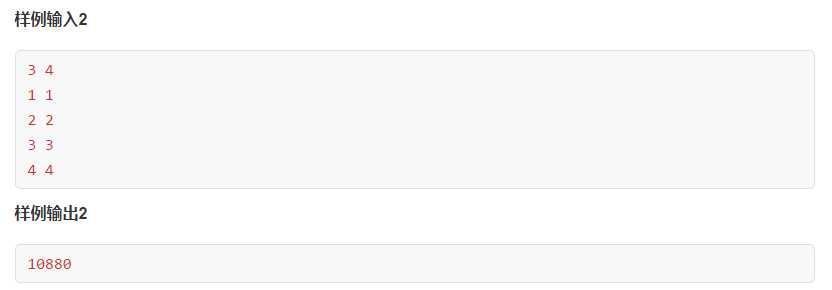
  1 #include<iostream>
  2 using namespace std;
  3 typedef long long ll;
  4 #define MOD 1000000007
  5 struct matrix
  6 {
  7     long long arr[8][8];
  8 };
  9 matrix unit()
 10 {
 11     matrix C;
 12     for(int i=1;i<7;i++)
 13     {
 14         for(int j=1;j<7;j++)
 15         {
 16             if(i==j)
 17             {
 18                 C.arr[i][j]=1;
 19             }
 20             else
 21             {
 22                 C.arr[i][j]=0;
 23             }
 24         }
 25     }
 26     return C;
 27 }
 28 matrix matrix_mul(matrix A,matrix B,ll mod)
 29 {
 30     matrix C;
 31     for(int i=1;i<7;i++)
 32     {
 33         for(int j=1;j<7;j++)
 34         {
 35             C.arr[i][j]=0;
 36             for(int k=1;k<7;k++)
 37             {
 38                 C.arr[i][j]+=A.arr[i][k]*B.arr[k][j]%mod;
 39                 C.arr[i][j]%=mod;
 40             }
 41         }
 42     }
 43     return C;
 44 }
 45 matrix matrix_pow(matrix A,ll n,ll mod)
 46 {
 47     matrix res=unit();
 48     matrix temp=A;
 49     for(;n;n/=2)
 50     {
 51         if(n&1)
 52         {
 53             res=matrix_mul(res,temp,mod);
 54         }
 55         temp=matrix_mul(temp,temp,mod);
 56     }
 57     return res;
 58 }
 59 long long pow_mod(ll num,ll n,ll mod)
 60 {
 61     ll res=1;
 62     ll temp=num;
 63     for(;n;n/=2)
 64     {
 65         if(n&1)
 66         {
 67             res=res*temp%mod;
 68         }
 69         temp=temp*temp%mod;
 70     }
 71     return res;
 72 }
 73 int Parner[7] = {0,4,5,6,1,2,3};
 74 int main()
 75 {
 76     ll n,m;
 77     int a,b;
 78     cin>>n>>m;
 79     matrix complict;
 80     for(int i=1;i<7;i++)
 81     {
 82         for(int j=1;j<7;j++)
 83         {
 84             complict.arr[i][j]=1;
 85         }
 86     }
 87     for(int i=0;i<m;i++)
 88     {
 89         cin>>a>>b;
 90         complict.arr[Parner[a]][b]=complict.arr[Parner[b]][a]=0;
 91     }
 92     matrix ini;
 93     for(int i=1;i<7;i++)
 94     {
 95         ini.arr[1][i]=1;
 96     }
 97     for(int i=2;i<7;i++)
 98     {
 99         for(int j=1;j<7;j++)
100         {
101             ini.arr[i][j]=0;
102         }
103     }
104 
105     ini=matrix_mul(ini,matrix_pow(complict,n-1,MOD),MOD);
106 
107     ll sum=0;
108     for(int i=1;i<7;i++)
109     {
110         sum+=ini.arr[1][i];
111         sum%=MOD;
112     }
113     ll o=pow_mod(4,n,MOD);
114     cout<<(sum*o)%MOD<<endl;
115     return 0;
116 }

View Code