主成分分析与因子分析

Posted 2020-08-31 immaculate

主成分分析，主成份是原始变量的线性组合，在考虑所有主成份的情况下主成份和原始变量间是可以逆转的。即“简化变量”，将变量以不同的系数合起来，得到好几个复合变量，然后在从中挑几个能表示整体的复合变量就是主成份，然后计算得分。

因子分析，公共因子和原始变量的关系是不可逆转的，但是可以通过回归得到。是将变量拆开，分成公共因子和特殊因子。过程是：因子载荷计算，因子旋转，因子得分。

主成份分析

主成份分析需要知道两变量之间的相关性，生成协方差举证和相关新矩阵，对应的生成的新向量矩阵Y还有特征值λi，对应是第I个新向量对总体信息的贡献率为λi/(λ1+λ2+...+λn),对应的还有一个累积贡献率。

确定主成份的个数的方法有：特征值大于1（要求原始数据的每一个变量至少能贡献1各单位的变异）、陡坡检验法（陡坡图中开始平坦的点之前的点的个数）、累积解释变异比例法（即（λ1+...+λi）/(λ1+λ2+...+λn)>70%）。

同时也可以知道主成分分析对应的几个难点①是使用协方差矩阵还是相关系数矩阵②如何确定主成份的个数。当数据中不同变量的度量单位不同并且数值相差较大就用标准化后的相关系数矩阵，当数值相差不大并且指标的权重不一样时，考虑用协方差矩阵。对于个数的确定就是我们一些边界问题是否1左右的也可以囊括进主成份中，是否难以确定开始变平坦的是那个点，是否70%不够。等几个问题。

主成分分析可以用两个过程步完成PROC FACTORS 、PROC PRINCOMP。后者能处理的数据量大一些，效率高一些，，前者输出的内容丰富些，还可以做旋转因子。

以下是主成分分析过程；

proc princomp data=sashelp.cars out=car_component;
    var mpg_city mpg_highway weight wheelbase length;
run;

输出结果：

先是输出统计结果，再是输出相关性矩阵，这里princomp步默认使用的是相关系数矩阵，实际应用过程中，可以通过cov选项来指定使用的矩阵。从一扇那个结果可以看出：highway和city、wheelbase和length和weight相关性较强。

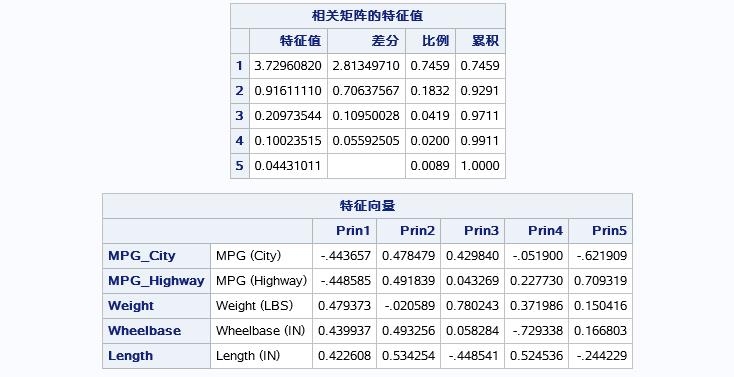
接下来是相关矩阵的特征值以及特征向量，可以看出前两个特征值的贡献率就已经发到了92%，所以前两个对用的特征向量就足以表达整体的92%了。可以得出第一主成份线性表达式为：PRIN1=-0.443657*CITY-0.44858*HIGHWAY+0.4793*WEIGHT+0.4399*WHEELBASE+0.4226*LENGHT,一次类推第二主成份表达式即可。

还输出陡坡图如下：

可以看出是从第三个点开始变平坦，所以此数据的只有两个主成分变量。

从输出数据集中可有主成分变量的打分状况。

 

其中有负分是因为计算主成份时用了标准化后的原始数据集。

接下来看FACTOR过程步：

proc factor data=sashelp.cars n=2  simple corr;
    var mpg_city mpg_highway weight wheelbase length;
run;

其中simple为输出常见的统计量，CORR输出相关性矩阵，N=2为保留两个主成分（这里是先进行过出成分分析结果已知主成分个数之后确定的两个，默认是输出一个，但是在没有先进行主成分分析的情况下也可以直接输出最大个数，即总变量的个数，然后再确定主成分个数）。输出结果如下：

 

 

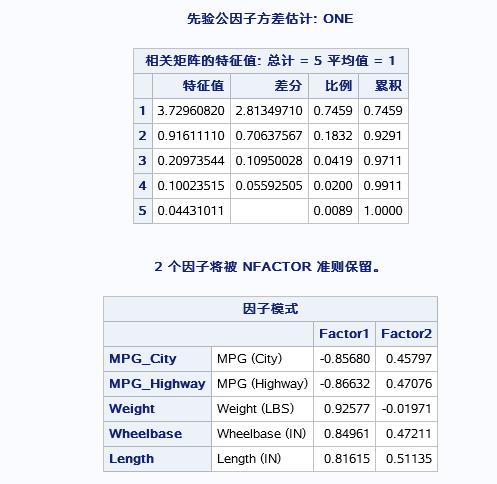
这里不一样的是：这里的主成分名称被因子替换了，并且指出有几个因子被保留，也给出了特征向量的贡献率。

这里得出的线性方程不于princomp过程的系数一致，原因是factor是假设所有因子或者主成份的方差为1，为princomp是方差为特征值，实际上可以转化过来；

现如下代码就于前面结果一致：

proc factor data=sashelp.cars n=5 score;
    ods output stdscorecoef=coef;
    var mpg_city mpg_highway weight wheelbase length;
run;
proc stdsize method=ustd mult=0.44721 data=coef out=eigenvectors;
    var factor1-factor5;
run;

输出的结果就会一致。

因子分析

对于主成分分析的目的是“降维”，而因子分析的目的通过“降维”，来找到能解释原始便能量的公共因子和特殊因子。

计算因子载荷的方法有：主成份分析法（即特征向量对应的值），极大似然法。

因子旋转有：正交旋转（公共因子间不相关）和斜交旋转。

proc factor data=sashelp.cars corr priors=smc rotate=varimax;
    var mpg_city mpg_highway weight wheelbase length;
run;

corr使用相关系数矩阵，priors=smc指明先验公因子估计方法为多元相关系数的平方。rotate=varimax为指明使用最大正交旋转法进行对因子的旋转。

输出结果和前面相似的有：

 

 

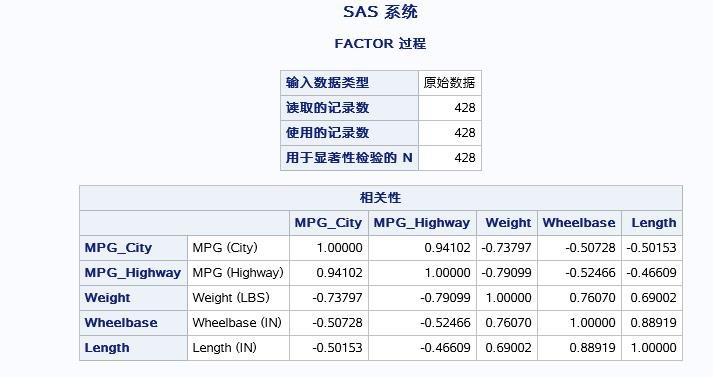
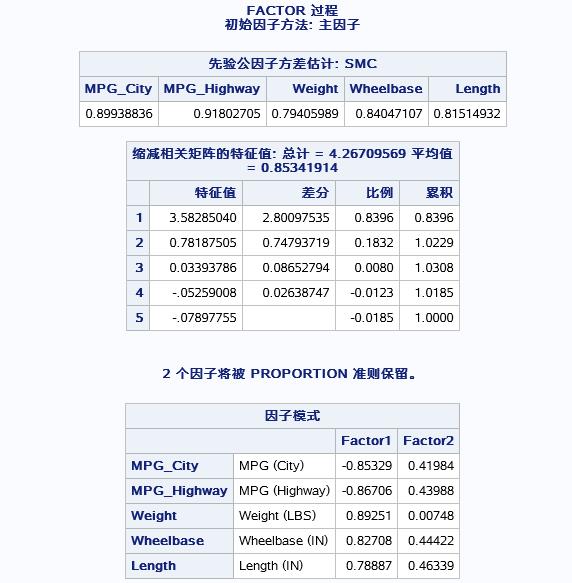
旋转之前各自变量均有载荷而且大部分载荷明显不利于对因子的意义进行解释，接下来就是用rotate=varimax是指明用最大正交旋转法对因子进行旋转，结果如下：

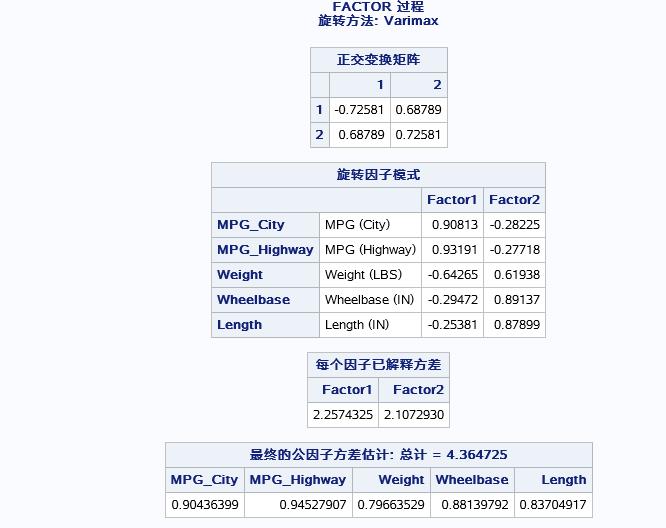
旋转之后的因子特征比较明显，高低载荷分明，除了weight不便归类外其余的factor1包含city和highway和weight三个变量可解释为“整车油耗”，factor可解释为“整车舒适”。接下来是用两公共因子进行得分计算，使用PROC SCORE过程即可满足：

 

proc factor data=sashelp.cars corr priors=smc rotate=varimax
    outstat=factcars score;
    var mpg_city mpg_highway weight wheelbase length;
run;

proc score data=sashelp.cars score=factcars out=fscore;
    var mpg_city mpg_highway weight wheelbase length;
run;

得到的打分后的数据集为：

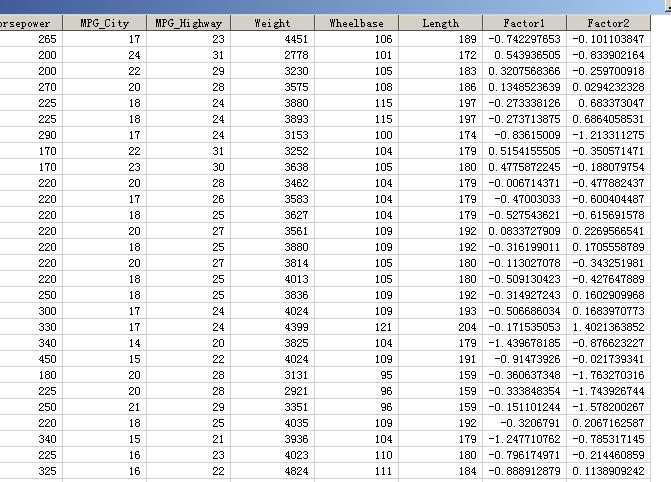
总结：主成分分析为：把变量合起来形成个数较少的新变量（简化变量），因子分析是把变量拆开（公共因子和特殊因子）即分析学生成绩由什么因子组成的。