POJ 3155 Hard Life（最大密度子图）

Posted 2020-08-30 forever97‘s blog

 

【题目链接】 http://poj.org/problem?id=3155

 

【题目大意】

　　公司内部共n个员工，员工之间可能两两合不来。
　　若员工u和员工v有矛盾，用边(u, v)表示，共m个矛盾。
　　突然大股东送来一个富二代，威胁到你的CEO宝座。
　　你想分配给富二代一个垃圾团队，使得团队成员间的不团结率最高。
　　不团结率定义为团队人员间的矛盾总数与被裁人员数的比值

     （不团结率=团队人员之间的矛盾总数/团队人员数）。

 

【题解】

　　题目要求即为：

　　　　

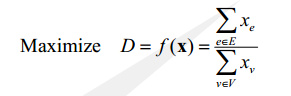
　　即求最大密度子图，可利用分数规划和最大权闭合图求解。

 

【代码】

#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
using namespace std;
const double INF=0x3fffffff;
const double eps=1e-8; 
const int MAX_V=110;
typedef double cap_type;
struct edge{
	  int to,rev;
	  cap_type cap;
	  edge(int to,cap_type cap,int rev):to(to),cap(cap),rev(rev){}
};
vector<edge> G[MAX_V];
int V,level[MAX_V],iter[MAX_V];
void add_edge(int from,int to,cap_type cap){
    G[from].push_back((edge){to,cap,G[to].size()});
    G[to].push_back((edge){from,0,G[from].size()-1});
}
void bfs(int s){
    memset(level,-1,sizeof(level));
    queue<int> que;
    level[s]=0;
    que.push(s);
    while(!que.empty()){
        int v=que.front(); que.pop();
        for(int i=0;i<G[v].size();i++){
            edge &e=G[v][i];
            if(e.cap>0&&level[e.to]<0){
                level[e.to]=level[v]+1;
                que.push(e.to);
            }
        }
    }
}
cap_type dfs(int v,int t,cap_type f){
    if(v==t)return f;
    for(int &i=iter[v];i<G[v].size();i++){
        edge &e=G[v][i];
        if(e.cap>0&&level[v]<level[e.to]){
            cap_type d=dfs(e.to,t,min(f,e.cap));
            if(d>0){
                e.cap-=d;
                G[e.to][e.rev].cap+=d;
                return d;
            }
        }
    }return 0;
}
cap_type max_flow(int s,int t){
    cap_type flow=0;
    for(;;){
        bfs(s);
        if(level[t]<0)return flow;
        memset(iter,0,sizeof(iter));
        cap_type f;
        while((f=dfs(s,t,INF))>0){
            flow+=f;
        }
    }
}
const int MAX_M=1010;
const int MAX_N=100;
int N,M,x[MAX_M],y[MAX_M],D[MAX_N];
void construct_graph(int s,int t,cap_type g){
	  for(int i=0;i<MAX_V;i++)G[i].clear();
	  for(int i=0;i<N;i++){
		    add_edge(s,i,M);
		    add_edge(i,t,M+2*g-D[i]);
	  }
	  for(int i=0;i<M;i++){
		    add_edge(x[i]-1,y[i]-1,1.0);
		    add_edge(y[i]-1,x[i]-1,1.0);
	  }
}
int leftv,vis[MAX_V];
void cal_res_net(int v){
    ++leftv;
	  vis[v]=1;
	  for(int i=0;i<G[v].size();i++){
		    edge &e=G[v][i];
		    if(e.cap>eps&&!vis[e.to])cal_res_net(e.to);
	  }
}
void init(){
    memset(D,0,sizeof(D));
    for(int i=0;i<M;i++){
        scanf("%d%d",&x[i],&y[i]);
        D[x[i]-1]++; D[y[i]-1]++;
    }
}
void solve(){
    if(M==0){printf("%d\\n%d\\n",1,1);return;} 
    int s=N,t=N+1;
    double l=0,r=M,mid,tmp;
    const double Limit=1.0/N/N;
    while(r-l>=Limit){
        mid=(l+r)/2;
        construct_graph(s,t,mid);
        tmp=(N*M-max_flow(s,t))/2;
        (tmp>eps?l:r)=mid;
    }construct_graph(s,t,l);
    max_flow(s,t);
    leftv=0;
    cal_res_net(s);
    printf("%d\\n",leftv-1);
    for(int i=0;i<N;i++)if(vis[i])printf("%d\\n",i+1);
}
int main(){
    while(~scanf("%d%d",&N,&M)){
        init();
        solve();
    }return 0;
}