svm支持向量机系列 -- 线性支持向量机

Posted 2020-08-29 罐装可乐

1、主要内容

　　沿着之前学些机器学习基石课程中学习到的工具进行分析，该工具主要就是vc维，沿着特征转换这一目标进行探讨：

　　

　　(1)、当数据的特征的数量很大时，如何进行特征转换？支撑向量机

　　(2)、能不能找到具有预测性的特征然后联合起来？

　　

　　(3)、如何发现隐藏的具有预测意义的特征？原先的神经网络到现在的深度学习技术。

　　 

　　这节课主要讲述svm的由来，背后的原理，最佳化的求解问题。

2、线性支持向量机的由来

　　(1)、从线性分类器说起到svm问题的提出

　　如果数据线性可分，那么必然可以找到一条线对齐进行分类，计算特征向量的各分量与其相应的权重相乘后得到一个总的评分后，经过一个符号函数输出分类结果。

　　

　　线性分类器的超平面为：

　　　　

　　符合以上的超平面有很多，那么哪一条是最好？怎么衡量的这个好坏？

　　

　　对于PLA来说，以上的三条线都是可能的，因为PLA是随机挑选一条线然后根据数据进行逐个优化，因此学习的结果是随机的不确定的。

　　根据vc bound理论，期望误差会被经验误差与一个复杂度所bound住：

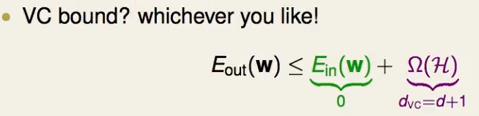　　(Ω(Η) = 4*(2N)d^_vc*exp(1/8*ε²N)对ε进行反解)

　　经过之前的证明可以该复杂度与hypothesis set的vc维有关系，这样看这三条线貌似都可以。但是直觉说第三个可能好一点，因为这个线与训练的数据的点距离比较远。

　　下面对其进行一个简单的说明：

　　我们搜集到的资料都是带有一定误差的，假设原有的训练数据为x_n，后来采集的相似的数据为x，如图：

　　

　　这就说如果原有的分类器距离点比较近就像图一和图二所示，误差很小的情况下就可能引起错误，因此这里说所有的点离这个分界面越远越好。

　　

　　那么在明确这一选择要求后，采取一下措施在选择时挑选出一个最优的选择：

　　

　　对于已经正确分类的hypothesis set中选择边界最大的那条作为最终的选择结果，如何对此进行最优化选择？在PLA以及logistic regression中我们最后只能得出一条线，不能得出所有满足条件的线，也就没有办法先使用PLA或者logistic 回归之后再去选择最大的边界的线，那如何进行最优化求解？

　　注意到在以上的约束条件中距离是个很重要的因素，那么距离应该如何表示？

　　在之前的推导中我们都将bias 作为w向量的一部分，然后在特征中加上一个x0；现在我们不这样做，不添加x0并且bias单独拿出来：

　　

　　这样的话，h(x) :

　　

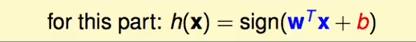
　　因此，我们求距离：

　　

　　就是点到面的计算公式：

　　

　　对于分离面来说还有一个性质就是：

　　

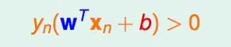
　　那么结合上面的距离计算公式，可以利用上面的分离面的性质结合到一起：

　　

　　那么上面的最优化的问题就可以简化为：

　　

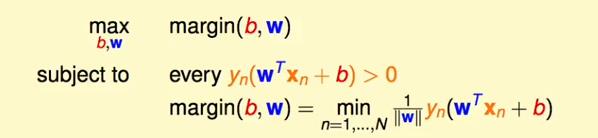
　　更进一步的，一个超平面乘以一个系数后还是原来的超平面，那么我们就可以使：

　　

　　最后得到一个这样的优化问题：

　　

　　(1)、约束条件：；

　　(2)、w向量的模值倒数的最大值，这个w向量就是所求的结果。

　　最后在对条件进行放宽，使得在n中求最小值，变成在对所有的n都有以下的条件：

　　

 　　同样上面的放宽可以保证上面的W的最终解在上面的未放宽的条件下的解相同。

3、标准化的问题求解

　　标准问题如下：

　　

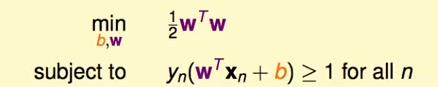
　　以特殊情况求解为例：

　　

 

　　假设w向量为w₁,w₂，b进行计算：

　　

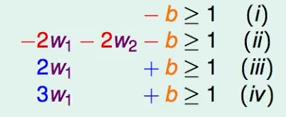
　　根据以上不等式可以得出一下结果：

　　

　　最后得出最后的目标函数就称为：

　　

4、什么是支撑向量机

　　上面的部分中引入了支撑向量机，什么是支撑向量机？再看上面的求解：

　　

　　在上面的例子中我们看找到了最后的那个fattest的那条线后，圈着的几个点一旦确定后，那么这条线的宽度就已经确定，那么除了离最近的线之外的点后其他的点对这个线的宽度就没有影响。

　　这个线段的位置和宽度由离着最近的点所唯一确定，其他的点来说就不是怎么需要了，这些点就称为支撑向量；

　　

　　而支撑向量机就是寻找这个支撑向量然后找到最宽的线的模型；

　　

　　解决一般的支持向量机问题：有限制条件下的优化问题

　　

　　在使用梯度下降时， 在有限制的情况下，梯度下降就不能使用了，因此此时使用二次规划方法解决：

　　

5、二次规划问题