Codeforces Round #394 div2

Posted 2020-08-29

A. Dasha and Stairs（数学）

http://codeforces.com/problemset/problem/761/A

 

题意：已知有a个偶数b个奇数，判断这些数能不能组成连续正整数数列。

 

算法：直接判断abs(a-b)≦1即可。注意a和b同时为0的情况。

 

代码：

#include<bits/stdc++.h>
#define REP(i, L, R) for(int i=L; i<=R; i++)
#define MST(A, x) memset(A, x, sizeof(A)) 
using namespace std;
typedef long long LL;
int main()
{
    int a, b;
    scanf("%d%d", &a, &b);
    if (a == 0 && b == 0) printf("NO");
    else
        if (abs(a-b) <= 1) printf("YES");
        else printf("NO");
    return 0;
}

 

B. Dasha and friends（枚举）

http://codeforces.com/problemset/problem/761/B

 

题意：已知一个长度为m的圆上有m个均匀的点，两个数列（到出发点的距离）分别描述两个走法，判断这两个走法能否重合。

 

算法：枚举两个走法的出发点，模拟判断即可。

 

代码：

#include<bits/stdc++.h>
#define REP(i, l, r) for(int i=l; i<=r; i++)
#define MST(A, x) memset(A, x, sizeof(A)) 
using namespace std;
typedef long long LL;
const int MAXN = 50+10;
const int MAXL = 100+10;
int n, L;
int a[MAXN], b[MAXN];
int main()
{
    scanf("%d %d", &n, &L);
    REP(i, 1, n) scanf("%d", &a[i]);
    REP(i, 1, n) scanf("%d", &b[i]);
    bool flag = false;
    REP(i, 0, L-1)
        REP(j, 0, L-1)
        {
            bool f[MAXL];
            MST(f, 0);
            REP(k, 1, n)
            {
                f[(i+a[k]) % L] = 1;
                f[(j+b[k]) % L] = 1;
            }
            int cnt = 0;
            REP(k, 0, L-1)
                if (f[k]) cnt++;
            if (cnt == n) 
            {
                flag = true;
                break;
            }
        }
    if (flag) printf("YES");
    else printf("NO");
    return 0;
}

 

C. Dasha and Password（枚举）

http://codeforces.com/problemset/problem/761/C

 

题意：已知n个长度为m的字符串（看作环），每个字符串的首字符上有一个指针，可以通过一次操作使指针左移或右移一位，求最少多少次操作可使这n个指针指向的字符构成一个合法字符串（即存在特殊符号#*&其一、数字和小写字母）。

 

算法：枚举数字、字母和特殊符号分别取自哪一个字符串，计算需要操作次数并取最小值即可。

 

代码：

#include<bits/stdc++.h>
#define REP(i, l, r) for(int i=l; i<=r; i++)
#define MST(A, x) memset(A, x, sizeof(A)) 
using namespace std;
typedef long long LL;
const int MAXN = 50+10;
int n, m;
char str[MAXN][MAXN];
int pointer(int dlta)
{
    if (dlta < 0) return dlta+m;
    if (dlta >= m) return dlta-m;
    return dlta;
}
bool isDigit(char c)
{
    if (c>=‘0‘ && c<=‘9‘) return 1; else return 0;
}
bool isLetter(char c)
{
    if (c>=‘a‘ && c<=‘z‘) return 1; else return 0;
}
bool isSymbol(char c)
{
    if (c==‘#‘ || c==‘*‘ || c==‘&‘) return 1; else return 0;
}
int cal(int a, int b, int c)
{
    int ret = 0;
    bool flag = false;
    REP(d, 0, m-1)
        if (isDigit(str[a][pointer(d)]) || isDigit(str[a][pointer(-d)]))
        {ret += d;    flag = true;    break;}
    if (!flag) ret += m;
    
    flag = false;
    REP(d, 0, m-1)
        if (isLetter(str[b][pointer(d)]) || isLetter(str[b][pointer(-d)]))
        {ret += d;    flag = true;    break;}
    if (!flag) ret += m;
    
    flag = false;
    REP(d, 0, m-1)
        if (isSymbol(str[c][pointer(d)]) || isSymbol(str[c][pointer(-d)]))
        {ret += d;    flag = true;    break;}
    if (!flag) ret += m;
    
    return ret;
}
int main()
{
    scanf("%d %d", &n, &m);
    REP(i, 1, n) scanf("%s", str[i]);
    int res = 1<<25;
    REP(i, 1, n)
        REP(j, 1, n)
            REP(k, 1, n)
                if (i!=j && j!=k && k!=i) res = min(res, cal(i, j, k));
    printf("%d", res);
    return 0;
}

 

D. Dasha and Very Difficult Problem（贪心）

http://codeforces.com/problemset/problem/761/D

 

题意：已知三组数a,b,c满足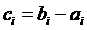且c中个元素互不相同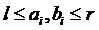，。给出数组a和数组p（描述数组c中个元素大小且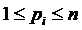），求任意一个可行的数组b；若无解则输出-1。

 

算法：我们有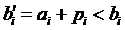，可以求出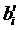的上界upper和下届lower。若upper-lower>r-l，则无解；否则根据lower和l的差调整即可。

 

代码：

#include<bits/stdc++.h>
#define REP(i, L, R) for(int i=L; i<=R; i++)
using namespace std;
const int MAXN = 1e5+10;
const int MAXX = 1e9+10;
int n, l, r;
int a[MAXN], b[MAXN], p[MAXN];
int main()
{
    scanf("%d %d %d", &n, &l, &r);
    REP(i, 1, n) scanf("%d", &a[i]);
    int lower = MAXX;
    int upper = 0;
    REP(i, 1, n) 
    {
        scanf("%d", &p[i]);
        b[i] = a[i] + p[i];
        lower = min(lower, b[i]);
        upper = max(upper, b[i]);
    }
    if (upper-lower > r-l) printf("-1");
    else
    {
        int delta = l - lower;
        REP(i, 1, n) 
        {
            b[i] += delta;
            printf("%d ", b[i]);
        }
    }
    return 0;
}

 

E. Dasha and Puzzle（DFS）

http://codeforces.com/problemset/problem/761/E

 

题意：已知一棵n个节点的树，判断能否将其放在笛卡尔坐标系中，使得每条边都平行于坐标轴且互不相交。

 

算法：首先，易知任意点的度数一定小于等于4，否则一定不能放在笛卡尔坐标系中。下面我们只需要从根节点开始深搜就可以了。因为题目要求可行解，我们将边长从2^58每次缩短一半即可。

 

代码：

#include<bits/stdc++.h>
#define REP(i, L, R) for(int i=L; i<=R; i++)
#define MST(A, x) memset(A, x, sizeof(A))
using namespace std;
typedef long long LL;
const int MAXN = 30+10;
const LL MAXX = 1e18+10;
const int DX[5] = {0, 1, -1, 0, 0};
const int DY[5] = {0, 0, 0, 1, -1};
int n;
int G[MAXN][MAXN];
int degree[MAXN], father[MAXN];
LL x[MAXN], y[MAXN];
int index(int k)
{
    if(k == 1) return 2;
    if(k == 2) return 1;
    if(k == 3) return 4;
    if(k == 4) return 3;
}
void DFS(int u, LL len, int k)
{
    REP(i, 1, degree[u])
        if(k && G[u][i]==father[u]) swap(G[u][i], G[u][index(k)]);
    REP(i, 1, degree[u])
    {
        int v = G[u][i];
        if (v == father[u]) continue;
        x[v] = x[u] + len*DX[i];
        y[v] = y[u] + len*DY[i];
        father[v] = u;
        DFS(v, len>>1, i);
    }
}
int main()
{
    scanf("%d", &n);
    bool over = false;
    REP(i, 1, n-1)
    {
        int u, v;
        scanf("%d %d", &u, &v);
        G[u][++degree[u]] = v;
        G[v][++degree[v]] = u;
        if (degree[u]>4 || degree[v]>4)
        {
            printf("NO");
            over = true;
            break;
        }
    }
    if (!over)
    {
        printf("YES\\n");
        x[1] = y[1] = 0;
        father[1] = 1;
        DFS(1, 1LL<<58, 0);
        REP(i, 1, n) printf("%I64d %I64d\\n", x[i], y[i]);
    }
    return 0;
}