贝塞尔曲线的使用

Posted 2020-08-28 丶笑看退场

什么是贝塞尔曲线

它主要用在Andorid中某些自定义VIew的时候需要绘制某些曲线。它只要有些名词介绍：

• 数据点:通常指一条路径的起始点和终止点
• 控制点：控制点决定可一条路径的弯曲轨迹，根据控制的点的个数，贝塞尔曲线被分为一阶贝塞尔曲线（0个控制点）、二阶贝塞尔曲线（1个控制点）、三阶贝塞尔曲线（2个控制点）

在平时开发中主要掌握二阶和三阶贝塞尔曲线

二阶贝塞尔曲线

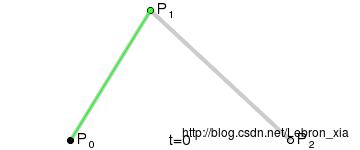
由上图看，P0是起点，P2是终点。P1是控制点，t是一个系数，表示从0-1的变化过程，红色的线就是最终画出的曲线。其中主要是用到了quaTo()这个方法。

• 实现代码如下

public class SecondOrderBezier extends View {

    //辅助线
    private Paint mPaintAuxiliary;
    //控制点名称
    private Paint mPaintAuxiliaryText;
    //贝塞尔曲线
    private Paint mPaintBezier;

    //控制点坐标
    private float mAuxiliaryX;
    private float mAuxiliaryY;

    //起始点坐标
    private float mStartPointX;
    private float mStartPointY;
    //终点坐标
    private float mEndPointX;
    private float mEndPiuntY;

    private Path mPath = new Path();

    public SecondOrderBezier(Context context) {
        super(context);
    }

    public SecondOrderBezier(Context context, AttributeSet attrs) {
        super(context, attrs);
        mPaintBezier = new Paint(Paint.ANTI_ALIAS_FLAG);
        mPaintBezier.setStyle(Paint.Style.STROKE); //设置画笔为空心
        mPaintBezier.setStrokeWidth(8);

        mPaintAuxiliary = new Paint(Paint.ANTI_ALIAS_FLAG);
        mPaintAuxiliary.setStyle(Paint.Style.STROKE);
        mPaintAuxiliary.setStrokeWidth(2);

        mPaintAuxiliaryText = new Paint(Paint.ANTI_ALIAS_FLAG);
        mPaintAuxiliaryText.setStyle(Paint.Style.STROKE);
        mPaintAuxiliaryText.setTextSize(20);
    }

    public SecondOrderBezier(Context context, AttributeSet attrs, int defStyleAttr) {
        super(context, attrs, defStyleAttr);
    }

    @Override
    protected void onSizeChanged(int w, int h, int oldw, int oldh) {
        super.onSizeChanged(w, h, oldw, oldh);

        //起始和终点的坐标
        mStartPointX = w / 4;
        mStartPointY = h /2 - 200;

        mEndPointX = w / 4 * 3;
        mEndPiuntY = h /2 - 200;
    }

    @Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);
        //重置绘制路线
        mPath.reset();
        //mpath绘制的绘制起点
        mPath.moveTo(mStartPointX, mStartPointY);
        //绘制辅助控制点
       canvas.drawPoint(mAuxiliaryX, mAuxiliaryY, mPaintAuxiliary);
        canvas.drawText("控制点", mAuxiliaryX, mAuxiliaryY, mPaintAuxiliaryText);
        canvas.drawText("起始点", mStartPointX, mStartPointY, mPaintAuxiliaryText);
        canvas.drawText("终止点", mEndPointX, mEndPiuntY, mPaintAuxiliaryText);

        //辅助线
        canvas.drawLine(mStartPointX, mStartPointY, mAuxiliaryX, mAuxiliaryY, mPaintAuxiliary);
        canvas.drawLine(mEndPointX, mEndPiuntY, mAuxiliaryX, mAuxiliaryY, mPaintAuxiliary);
        //二阶贝塞尔、线，实现绘制贝塞尔平滑曲线；previousX, previousY为操作点，cX, cY为终点
        mPath.quadTo(mAuxiliaryX, mAuxiliaryY, mEndPointX, mEndPiuntY);
        canvas.drawPath(mPath, mPaintBezier);
    }

    @Override
    public boolean onTouchEvent(MotionEvent event) {
        switch (event.getAction()){
            case MotionEvent.ACTION_MOVE:
                mAuxiliaryX = event.getX();
                mAuxiliaryY = event.getY();
                //更新绘制
                invalidate();
        }
        return true;
    }
}

三阶贝塞尔曲线

三阶贝塞尔曲线主要是多了一个控制点，指定一个起点和一个终点，再指定两个控制点即可实现,主要是用到了Path对象的cubicTo()方法。

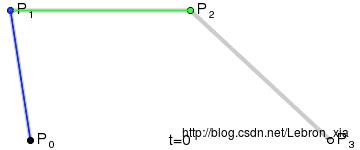
• 实现代码如下，很多于二阶雷同：

  @Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);

        mPath.reset();

        mPath.moveTo(mStartPointX, mStartPointY);

        // 辅助点
        canvas.drawPoint(mAuxiliaryOneX, mAuxiliaryOneY, mPaintAuxiliary);
        canvas.drawPoint(mAuxiliaryTwoX, mAuxiliaryTwoY, mPaintAuxiliary);
        canvas.drawText("控制点1", mAuxiliaryOneX, mAuxiliaryOneY, mPaintAuxiliaryText);
        canvas.drawText("控制点2", mAuxiliaryTwoX, mAuxiliaryTwoY, mPaintAuxiliaryText);
        canvas.drawText("起始点", mStartPointX, mStartPointY, mPaintAuxiliaryText);
        canvas.drawText("终止点", mEndPointX, mEndPointY, mPaintAuxiliaryText);
        mPath.cubicTo(mAuxiliaryOneX, mAuxiliaryOneY, mAuxiliaryTwoX, mAuxiliaryTwoY, mEndPointX, mEndPointY);
        // 辅助线
        canvas.drawLine(mStartPointX, mStartPointY, mAuxiliaryOneX, mAuxiliaryOneY, mPaintAuxiliary);
        canvas.drawLine(mEndPointX, mEndPointY, mAuxiliaryTwoX, mAuxiliaryTwoY, mPaintAuxiliary);
        //三阶贝塞尔曲线
        canvas.drawLine(mAuxiliaryOneX, mAuxiliaryOneY, mAuxiliaryTwoX, mAuxiliaryTwoY, mPaintAuxiliary);
        canvas.drawPath(mPath, mPaintBezier);
    }

其中有些情况下需要自己设置动画的路径效果，来实现炫酷的效果，就没有封装好的方法，需要自己使用公式：

public class BezierUtil {
    /**
     * 二阶贝塞尔曲线公式
     * B(t) = (1 - t)^2 * P0 + 2t * (1 - t) * P1 + t^2 * P2, t ∈ [0,1]
     *
     * @param t  曲线长度比例
     * @param p0 起始点
     * @param p1 控制点
     * @param p2 终止点
     * @return t对应的点
     */
    public static PointF CalculateBezierPointForQuadratic(float t, PointF p0, PointF p1, PointF p2) {
        PointF point = new PointF();
        float temp = 1 - t;
        point.x = temp * temp * p0.x + 2 * t * temp * p1.x + t * t * p2.x;
        point.y = temp * temp * p0.y + 2 * t * temp * p1.y + t * t * p2.y;
        return point;
    }

    /**
     * 三阶贝塞尔曲线公式
     * B(t) = P0 * (1-t)^3 + 3 * P1 * t * (1-t)^2 + 3 * P2 * t^2 * (1-t) + P3 * t^3, t ∈ [0,1]
     *
     * @param t  曲线长度比例
     * @param p0 起始点
     * @param p1 控制点1
     * @param p2 控制点2
     * @param p3 终止点
     * @return t对应的点
     */
    public static PointF CalculateBezierPointForCubic(float t, PointF p0, PointF p1, PointF p2, PointF p3) {
        PointF point = new PointF();
        float temp = 1 - t;
        point.x = p0.x * temp * temp * temp + 3 * p1.x * t * temp * temp + 3 * p2.x * t * t * temp + p3.x * t * t * t;
        point.y = p0.y * temp * temp * temp + 3 * p1.y * t * temp * temp + 3 * p2.y * t * t * temp + p3.y * t * t * t;
        return point;
    }
}

最后来一个示例：实现贝塞尔曲线购物车效果：
有两种方法：

1. 二阶贝塞尔曲线公式算出路径差值：
   核心代码

 /**
     * 添加商品到购物车里
     * @param goodsImageView
     */
    private void addGoodsToCart(ImageView goodsImageView) {
        //创造出执行动画的主题goodsImg
        final ImageView goods = new ImageView(this);
        goods.setImageDrawable(goodsImageView.getDrawable());

        RelativeLayout.LayoutParams parms = new RelativeLayout.LayoutParams(100, 100);
        mRlyShoppingCartRly.addView(goods, parms);

        //得到父布局的起始点坐标
        int[] parentLocation = new int[2];
        mRlyShoppingCartRly.getLocationInWindow(parentLocation);
        //得到商品图片坐标
        int startLoc[] = new int[2];
        goodsImageView.getLocationInWindow(startLoc);
        //得到购物车图片的坐标
        int endLoc[] = new int[2];
        mIvShoppingCart.getLocationInWindow(endLoc);

        //得到开始掉落商品的起始坐标
        float startX = startLoc[0] - parentLocation[0] + goodsImageView.getWidth() / 2;
        float startY = startLoc[1] - parentLocation[1] + goodsImageView.getHeight() / 2;
        //得到商品掉落的终点坐标
        float toX = endLoc[0] - parentLocation[0] + goodsImageView.getWidth() / 5;
        float toY = endLoc[1] - parentLocation[1];

        float mContorlPointX = (startX + toX)/2;
        float mContorlPointY = startY;
        Path mPath = new Path();
        mPath.reset();

        //第一步先移动到起始位置
        mPath.moveTo(startX,startY);
        //开始绘制贝塞尔曲线
        mPath.quadTo( mContorlPointX, mContorlPointY, toX, toY);
        //贝塞尔曲线的插值器
        BezierEvaluator bezierEvaluator = new BezierEvaluator(new PointF(mContorlPointX, mContorlPointY));
        // 属性动画实现
        ValueAnimator anim = ValueAnimator.ofObject(bezierEvaluator,new PointF(startX, startY),
                new PointF(toX, toY)
        );
        anim.setDuration(600);
        anim.addUpdateListener(new ValueAnimator.AnimatorUpdateListener() {
            @Override
            public void onAnimationUpdate(ValueAnimator valueAnimator) {
                PointF point = (PointF) valueAnimator.getAnimatedValue();
                //根据动画每帧小点移动所在的坐标
                goods.setTranslationX((int) point.x);
                goods.setTranslationY((int) point.y);
                //重绘
                mRlyShoppingCartRly.invalidate();
            }
        });

        anim.setInterpolator(new AccelerateDecelerateInterpolator());
        anim.start();

        // 动画结束后的处理
        anim.addListener(new Animator.AnimatorListener() {
            @Override
            public void onAnimationStart(Animator animator) {

            }

            @Override
            public void onAnimationEnd(Animator animator) {
                goodsCount ++;
                isShowCartGoodsCount();

                mTvShoppingCart.setText(String.valueOf(goodsCount));
                mRlyShoppingCartRly.removeView(goods);
            }

            @Override
            public void onAnimationCancel(Animator animator) {

            }

            @Override
            public void onAnimationRepeat(Animator animator) {

            }
        });

    }

1. 用PathMeasure路径测量
   PathMeasure看似很简单，但着实很有用，有了它，再结合上 Path 、Shader、ColorMatrix 等利器，我们已经可以做出很多酷炫的效果了
   核心代码

 /**
     * 添加商品到购物车
     * @author leibing
     * @createTime 2016/09/28
     * @lastModify 2016/09/28
     * @param goodsImg 商品图标
     * @return
     */
    private void addGoodsToCart(ImageView goodsImg) {
        // 创造出执行动画的主题goodsImg（这个图片就是执行动画的图片,从开始位置出发,经过一个抛物线（贝塞尔曲线）,移动到购物车里）
        final ImageView goods = new ImageView(this);
        goods.setImageDrawable(goodsImg.getDrawable());
        RelativeLayout.LayoutParams params = new RelativeLayout.LayoutParams(100, 100);
        mShoppingCartRly.addView(goods, params);

        // 得到父布局的起始点坐标（用于辅助计算动画开始/结束时的点的坐标）
        int[] parentLocation = new int[2];
        mShoppingCartRly.getLocationInWindow(parentLocation);

        // 得到商品图片的坐标（用于计算动画开始的坐标）
        int startLoc[] = new int[2];
        goodsImg.getLocationInWindow(startLoc);

        // 得到购物车图片的坐标(用于计算动画结束后的坐标)
        int endLoc[] = new int[2];
        mShoppingCartIv.getLocationInWindow(endLoc);

        // 开始掉落的商品的起始点：商品起始点-父布局起始点+该商品图片的一半
        float startX = startLoc[0] - parentLocation[0] + goodsImg.getWidth() / 2;
        float startY = startLoc[1] - parentLocation[1] + goodsImg.getHeight() / 2;

        // 商品掉落后的终点坐标：购物车起始点-父布局起始点+购物车图片的1/5
        float toX = endLoc[0] - parentLocation[0] + mShoppingCartIv.getWidth() / 5;
        float toY = endLoc[1] - parentLocation[1];

        // 开始绘制贝塞尔曲线
        Path path = new Path();
        // 移动到起始点（贝塞尔曲线的起点）
        path.moveTo(startX, startY);
        // 使用二阶贝塞尔曲线：注意第一个起始坐标越大，贝塞尔曲线的横向距离就会越大，一般按照下面的式子取即可
        path.quadTo((startX + toX) / 2, startY, toX, toY);
        // mPathMeasure用来计算贝塞尔曲线的曲线长度和贝塞尔曲线中间插值的坐标，如果是true，path会形成一个闭环
        mPathMeasure = new PathMeasure(path, false);

        // 属性动画实现（从0到贝塞尔曲线的长度之间进行插值计算，获取中间过程的距离值）
        ValueAnimator valueAnimator = ValueAnimator.ofFloat(0, mPathMeasure.getLength());
        valueAnimator.setDuration(500);

        // 匀速线性插值器
        valueAnimator.setInterpolator(new LinearInterpolator());
        valueAnimator.addUpdateListener(new ValueAnimator.AnimatorUpdateListener() {
            @Override
            public void onAnimationUpdate(ValueAnimator animation) {
                // 当插值计算进行时，获取中间的每个值，
                // 这里这个值是中间过程中的曲线长度（下面根据这个值来得出中间点的坐标值）
                float value = (Float) animation.getAnimatedValue();
                // 获取当前点坐标封装到mCurrentPosition
                // boolean getPosTan(float distance, float[] pos, float[] tan) ：
                // 传入一个距离distance(0<=distance<=getLength())，然后会计算当前距离的坐标点和切线，pos会自动填充上坐标，这个方法很重要。
                // mCurrentPosition此时就是中间距离点的坐标值
                mPathMeasure.getPosTan(value, mCurrentPosition, null);
                // 移动的商品图片（动画图片）的坐标设置为该中间点的坐标
                goods.setTranslationX(mCurrentPosition[0]);
                goods.setTranslationY(mCurrentPosition[1]);
            }
        });

        // 开始执行动画
        valueAnimator.start();

        // 动画结束后的处理
        valueAnimator.addListener(new Animator.AnimatorListener() {
            @Override
            public void onAnimationStart(Animator animation) {
            }

            @Override
            public void onAnimationEnd(Animator animation) {
                // 购物车商品数量加1
                goodsCount ++;
                isShowCartGoodsCount();
                mShoppingCartCountTv.setText(String.valueOf(goodsCount));
                // 把执行动画的商品图片从父布局中移除
                mShoppingCartRly.removeView(goods);
            }

            @Override
            public void onAnimationCancel(Animator animation) {
            }

            @Override
            public void onAnimationRepeat(Animator animation) {
            }
        });
    }

源码：源码

• 参考：
  Android 绘图贝塞尔曲线简单使用
  贝塞尔曲线开发的艺术
  安卓自定义View教程目录
  贝塞尔曲线之购物车动画效果