Dijkstra算法流程图

Posted 2023-04-01

如题

定义G=(V,E)，定义集合S存放已经找到最短路径的顶点，集合T存放当前还未找到最短路径的顶点，即有T=V-S

Dijkstra算法描述如下：

(1) 假设用带权的邻接矩阵edges来表示带权有向图，edges[i][j]表示弧<Vi, Vj>上的权值。若<Vi, Vj>不存在则置edges[i][j]=∞（计算机上用一个允许的最大值代替）。S为已经找到的从Vs出发的最短路径的终点集合，它初始化为空集。那么，从Vs出发到图上其余各顶点（终点）Vi可能达到的最短路径长度的初值为：D[i]=deges[s][i] Vi∈V

(2) 选择Vj，使得D[j]=MinD[i]|Vi∈V-S，Vj就是当前求得的一条从Vs出发的最短路径的终点。令S=S∪Vj

(3) 修改从Vs出发到集合V-S上任一顶点Vk可达的最短路径长度。如果D[j]+edges[j][k]<D[k]则修改D[k]为D[k]=D[j]+edges[j][k]

重复操作(2)(3)共n-1次。由此求得从Vs到图上其余各顶点的最短路径。 参考技术A 建议看下 严蔚敏 的那本《数据结构》，讲的挺明白的本回答被提问者采纳

课上Dijkstra算法练习

课上Dijkstra算法练习

Dijkstra算法，求解附图顶点A的单源最短路径,在纸上画出求解过程，上传截图。（注意图上要有自己的学号和姓名）

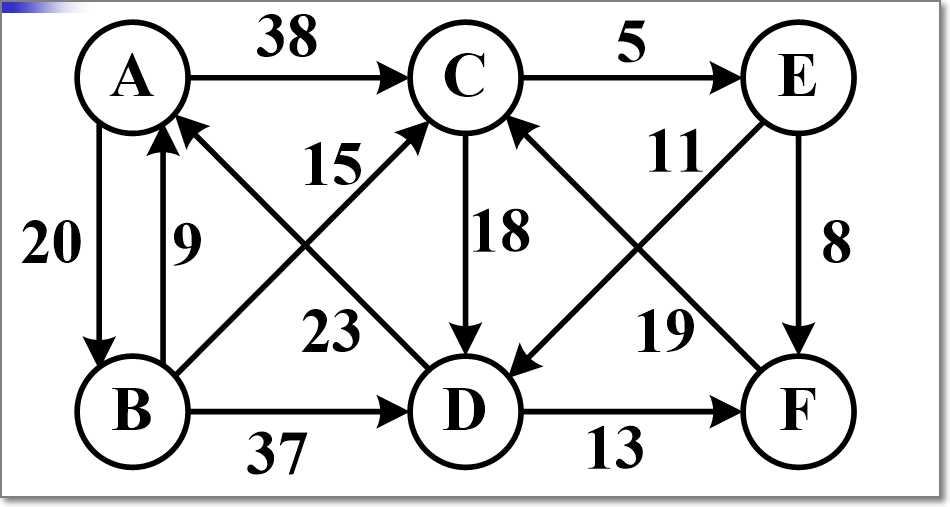
• 老师在上课时的ppt中讲解过程如下图：
  

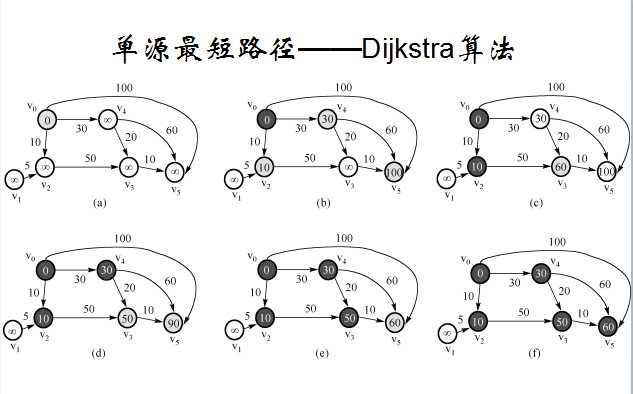
• 参考理解最短路径——迪杰斯特拉（dijkstra）算法,得出完整的算法原理。

  • ①首先，引入一个辅助向量D，它的每个分量D[i]表示当前所找到的 Dijkstra算法运行动画过程 Dijkstra算法运行动画过程 从起始点 （即源点 ）到其它每个顶点 的长度。例如，D[3] = 2表示从起始点到顶点3的路径相对最小长度为2。这里强调相对就是说在算法执行过程中D的值是在不断逼近最终结果但在过程中不一定就等于长度。

  • ②D的初始状态为：若从v 到v[i]有弧（即从v到v[i]存在连接边），则D[i]为弧上的权值（即为从v到v[i]的边的权值）；否则置D[i]为∞。显然，长度为 D[j]= Min{ D |v[i]∈V } 的路径就是从v出发到顶点v[j]的长度最短的一条路径，此路径为(v,v[j])。

  • ③那么，下一条长度次短的是哪一条呢？也就是找到从源点v到下一个顶点的最短路径长度所对应的顶点，且这条最短路径长度仅次于从源点v到顶点v[j]的最短路径长度。 假设该次短路径的终点是v[k]，则可想而知，这条路径要么是(v,v[k])，或者是(v,v[j],v[k])。它的长度或者是从v到v[k]的弧上的权值，或者是D[j]加上从v[j]到v[k]的弧上的权值。

  • ④一般情况下，假设S为已求得的从源点v出发的最短路径长度的顶点的集合，则可证明：下一条次最短路径（设其终点为x）要么是弧(v,x)，或者是从源点v出发的中间只经过S中的顶点而最后到达顶点 的路径。 因此，下一条长度次短的的最短路径长度必是D[j]= Min{ D[i] |v[i]∈V-S }，其中D 要么是弧( v,v[i])上的权值，或者是Di和弧(v[k] ,v[i] )上的权值之和。

• 那么看回这道题目，我起初的答案是下图，错在了...题目抄错了，很无语吧。
  

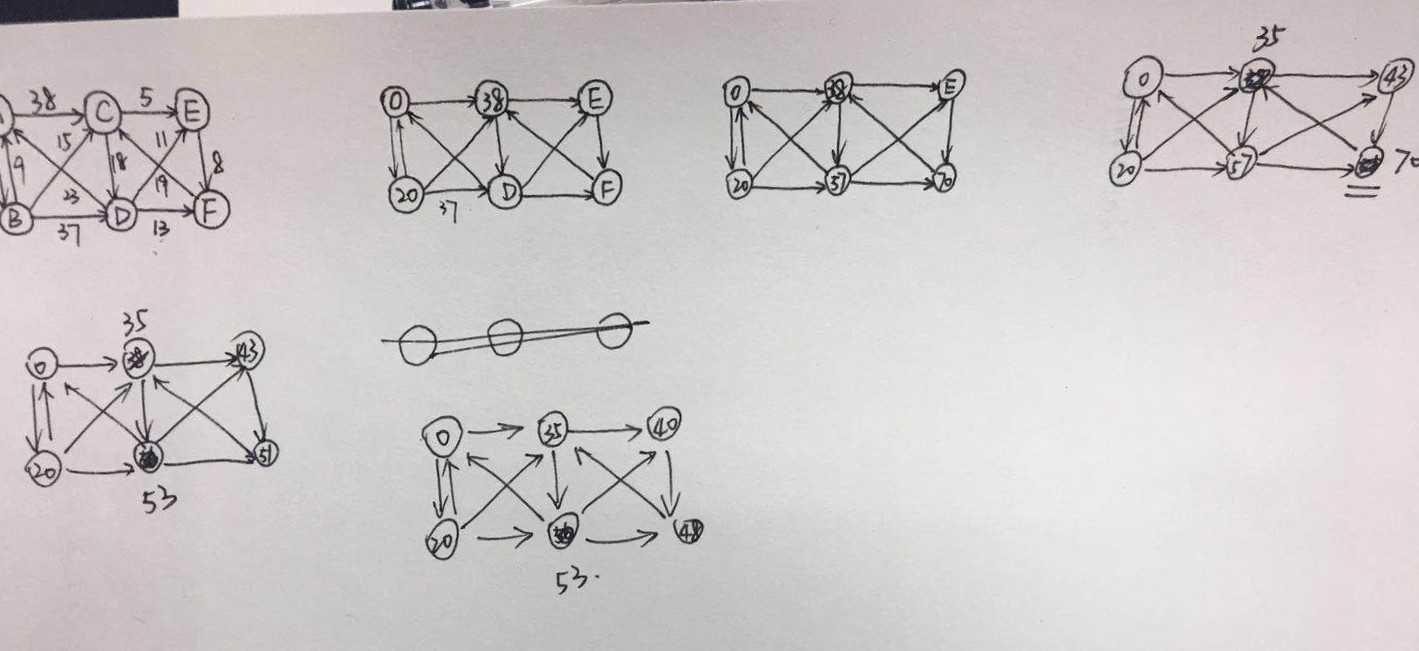
• 那么通过课下的学习，如何修改过程以及结果呢？
  

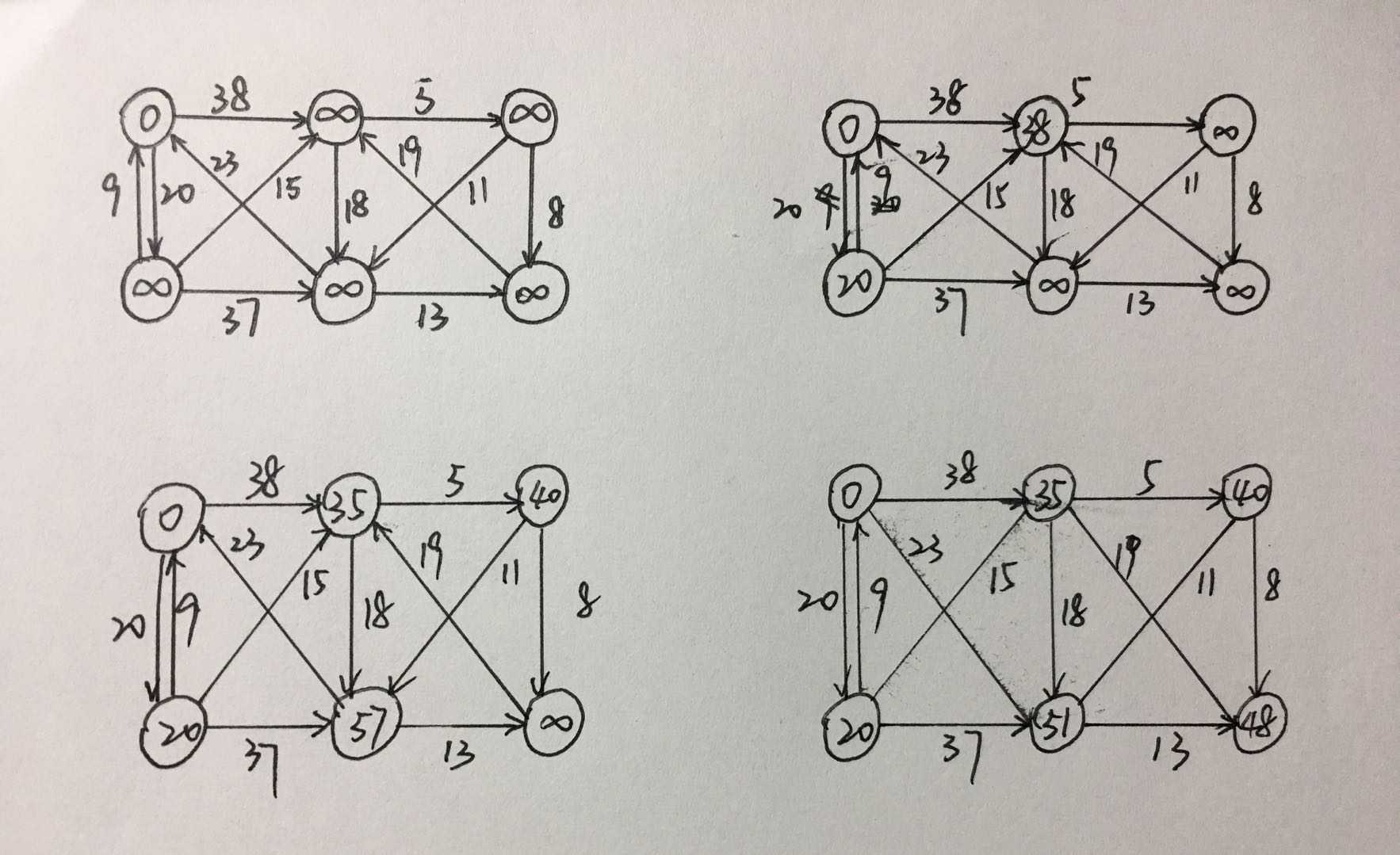
感想：

• 课堂上认真听讲努力消化，课下再花功夫搞清楚。但是题目抄错还是只有一次就够了(捂脸)。