关系运算 - 数据库系统原理

Posted 2020-08-26

       关系模型有三个重要组成部分：

1. 数据结构。数据库中全部数据及其相互联系都被组织成“关系”（二维表格）的形式。
2. 数据操纵。关系模型提供一组完备的高级关系运算，以支持对数据库的各种操作。关系运算又分为：关系代数和关系演算两类。
3. 数据完整性规则。数据库中数据必须满足实体完整性、参照完整性、用户定义完整性等三类完整性规则。

 

关系代数的五个基本操作

       关系代数是以关系（属性个数相同的元组的集合）为运算对象的一组高级运算的集合。关系代数的操作可以分为两类：

1. 传统的集合操作：并、差、交、笛卡尔积（乘法），笛卡尔积的逆运算（除法）。
2. 扩充的关系操作：对关系进行垂直分割（投影）、水平分割（选择）、关系的结合（连接，自然连接）。

• 并（Union）

       设关系 R 和 S 具有相同的关系模式，R 和 S 的并是由属于 R 或 属于 S 的元组构成的集合，记为 R ∪ S。

• 差（Difference）

       设关系 R 和 S 具有相同的关系模式，R 和 S 的差是由属于 R 但不属于 S 的元组构成的集合，记为 R - S。

• 笛卡尔积（Cartesian Product）

       设关系 R 和 S 的元数分别为 r 和 s，定义 R 和 S 的笛卡尔积是一个（r + s）元的元组集合，每个元组的前 r 个分量（属性值）来自 R 的一个元组，后 s 个分量来自 S 的一个元组，记为 R x S。若 R 有 m 个元组，S 有 n 个元组，则 R x S 有 m x n 个元组。

       例如：｛a，b｝，｛0，1，2｝的笛卡尔积是｛（a，0），（a，1），（a，2），（b，0），（b，1），（b，2）｝

• 投影（Projection）

       这个操作是对一个关系进行垂直分割，消去某些列，并重新安排列的顺序。例如 ABC 三列，选择 CA 两列并重新排序，记作 πCA（派符号，CA为下标），或者 π31（列序号）。

• 选择（Selection）

       根据某些条件对关系做水平分割，即选取符合条件的元组。书写时，运算常量用单引号括起来，属性序号或属性名不需要引号括起来。

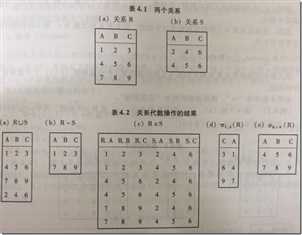
传统集合操作如下图：

 

关系代数的四个组合操作

• 交（Intersection）      

      关系 R 和 S 的交是由属于 R 又属于 S 的元组构成的集合，记为 R ∩ S。交操作的计算结果等于 R - （R - S）或 S - （S - R）。

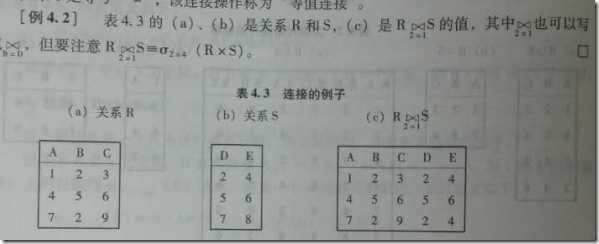
• 连接（Join）

       其实，就是从关系 R 和 S 的笛卡尔积中作选择操作。

      

• 自然连接（Natural join）

       一般，自然连接使用在 R 和 S 有公共属性的情况下，如果两个关系没有公共属性，那么其自然连接就转化为笛卡尔积操作。说白了，就类似数据库中两表基于主外键的 join 连接。

• 除法（Division）

       言语不太好描述这种操作，类似在一个主表中查找指定条件，且是充分满足多行多列的指定条件的结果，并且结果集上再做垂直分割，去除这个条件列。

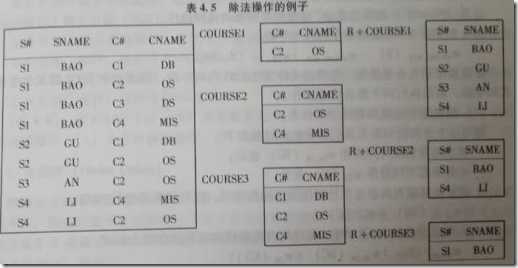
       下图的除法分别表示至少选修 COURSE1，COURSE2，COURSE3 中列出课程的学生名单：

      

 

关系代数运算的应用实例

       在关系代数运算中，把由五个基本操作经过有限次复合的式子称为关系代数表达式，这种表达式的运算结果仍是一个关系。

       例. 有这 4 个关系，用关系代数表达式表达每个查询语句。注：并(∪)、差(-)、笛卡尔积(×)、选择(σ)、投影(π) 、自然连接（??）、或（∨）、与（∧）

1. 教师关系 T（T#，TNAME，TITLE）
2. 课程关系 C（C#，CNAME，T#）
3. 学生关系 S（S#，SNAME，AGE，SEX）
4. 选课关系 SC（S#，C#，SCORE）

（1）检索学习课程号为 C2 课程的学生学号与成绩。

SELECT S#, SCORE FROM SC WHERE C# = ‘C2‘;  关系代数表达式：πS#,SCORE（σC#=‘C2‘（SC））

（2）检索学习课程号为 C2 课程的学生学号与姓名。

SELECT S#, SNAME FROM S INNER JOIN SC ON S.S# = SC.S# WHERE SC.C# = ‘C2‘;  关系代数表达式：πS#,SNAME（σC#=‘C2‘（S ?? SC））

（3）检索至少选修 LIU 老师所授课程中一门课程的学生学号和姓名。

πS#,SNAME（σTNAME=‘LIU‘（S ?? SC ?? C ?? T））

（4）检索选修课程号为 C2 或 C4 课程的学生学号。

πS#（σC#=‘C2‘ ∨ C#=‘C4‘ （SC））

（5）检索至少选修课程号为 C2 和 C4 课程的学生学号。

πS#（σC#=‘C2‘ ∧ C#=‘C4‘ （SC ?? SC）） 注：这里需要做关系自身的笛卡尔积操作，单个关系或表无法做一个字段的与操作。

（6）检索不学 C2 课程的学生姓名和年龄。

πSNAME,AGE（S） - πSNAME,AGE（σC#=‘C2‘（S ?? SC）） 注：先求出学习 C2 课程的学生姓名和年龄，再用全体学生和它做“减”操作。

（7）检索学习全部课程的学生姓名。

πS#,C#（SC） 表示学生选课情况；πC#（C） 表示全部课程；

学习了全部课程的学生学号可用除法操作表示，操作结果是学号 S# 集：πS#,C#（SC） ÷ πC#（C）；

最后做一个连接得到学生姓名：πSNAME（S ?? （πS#,C#（SC） ÷ πC#（C）））

（8）检索所学课程包含学号为 S3 的学生所学课程的学生学号。

πS#,C#（SC） ÷ πC#（σS#=‘S3‘（SC））

       关系代数表达式查询总结：一般，先把查询涉及到的关系取来，执行笛卡尔积或自然连接操作得到一张大的表格，然后再对其执行水平分割（选择操作）和垂直分割（投影操作）。但当查询涉及到否定或全部值时，就要用到（差）操作或（除法）操作了。

 

关系代数的两个扩充操作

• 外连接

       关系 R 和 S 做自然连接时，是建立在两个关系的公共属性上值相等的元组构成，这自然也会造成 R 或 S 中有些元组在操作时被舍弃。有时，可能需要保存这些被舍弃的元组，就需要做外连接。

       外连接又分为：外连接、左外连接、右外连接。连接后，空闲处填写 null。

• 外部并（Outer Union）

       之前定义的并操作要求 R 和 S 具有相同的关系模式。但如果 R 和 S 的关系模式不同，构成的新关系的属性由 R 和 S 的所有属性组成，公共属性只取一次，新关系的元组由 R 或 S 的元组构成，元组新增加的属性上填写空值，这种操作就是“外部并”操作。

 

关系演算

       关系演算可分为元组关系演算和域关系演算，前者以元组为变量，后者以属性为变量，简称元组演算和域演算。

• 元组关系演算

       t 是元组变量，表示一个元数固定的元组；P 是公式，在数理逻辑中也称为谓词，也就是计算机语言中的条件表达式。｛t | P（t）｝表示满足公式 P 的所有元组 t 的集合。

• 原子公式（Atoms）有 3 种形式：

1. R（s），其中 R 是关系名，s 是元组变量，它表示“s 是关系 R 的一个元组”。
2. s[i] θ u[j]，s 和 u 是元组变量，θ 是算术比较运算符，它表示“元组 s 的第 i 个分量和 u 第 j 个分量之间满足 θ 关系”。例如：s[1] < u[2]。
3. s[i] θ a 或 a θ u[j]，a 是常量，它表示“元组 s 的第 i 个分量值与常量 a 之间满足 θ 关系”。例如：s[1] = 3。

       在定义关系演算操作时，要用到“自由（Free）”和“约束（Bound）”变量概念。在一个公式中，如果元组变量未使用“存在量词（?）”或“全称量词（?）”符号定义，那么称其为“自由元组变量”，否则称其为“约束元组变量”。自由元组变量类似编程语言中外部变量或全局变量，约束元组变量类似过程中定义的局部变量。

• 公式（Formulas）的递归定义如下：

1. 每个原子是一个公式，其中的元组变量是自由变量。
2. 如果 P1 和 P2 是公式，那么 ┐P1、P1 ∨ P2、P1 ∧ P2、P1 => P2 也都是公式。分别表示：“P1 不是真”、“P1 或 P2 或两者都是真”、“P1 和 P2 都是真”、“若 P1 为真则 P2 必然为真”。
3. 如果 P1 是公式，那么（?s）（P1）和（?s）（P1）也都是公式。分别表示下列命题：“存在一个元组 s 使得公式 P1 为真”，“对于所有元组 s 都使得公式 P1 为真”。
4. 公式中各种运算符的优先级从高到低依次为：θ、? 和 ?、┐（符号：非），∨（符号：或） 和 ∧（符号：与），=>。
5. 公式只能由上述几种形式构成。

       在函数｛t | P（t）｝中，t 是 P（t）中唯一的自由元组变量。

 

       例. 下表的（a） 、（b）是关系 R 和 S，（c）~（e）分别是下面五个元组表达式的值：

1. R1 = ｛t | S（t）∧ t[1] > 2｝  解： t 是包含在 S 中的元组，且每一个 t 要满足的条件是 t[1] > 2，即 A 列的值大于 2。
2. R2 = ｛t | R（t）∧ ┐S（t）｝ 解：t 是包含在 R 中的元组，同时要满足非 S（t），即不是 S 中的元组。
3. R3 = ｛t | （?u）S（t）∧ R（u）∧ t[3] < u[2]｝  解：t 是包含在 S 中的元组，且 S.C < R.B 的才是符合要求的。

（a）表     R                          （b）表      S

A	B	C		A	B	C
1	2	3		1	2	3
4	5	6		3	4	6
7	8	9		5	6	9

（c）      R1                     （d）      R2                     （e）     R3

A	B	C		A	B	C		A	B	C
3	4	6		4	5	6		1	2	3
5	6	9		7	8	9		3	4	6

 

关系代数表达式到元组表达式的转换

       关系代数表达式可以等价的转换为元组表达式。由于所有的关系代数表达式都能用五个基本操作组合而成，因此，只要把五个基本操作能用元组演算表达式表达就行。例如：R ∪ S 可用 ｛t | R（t） ∨ S（t）｝表示；R – S 可用 ｛t | R（t） ∧ ┐S（t）｝表示。

 

关系运算的安全约束和等价性

       在数据库技术中，不产生无限关系和无穷验证的运算称为 安全运算，相应的表达式称为 安全表达式，所采取的措施称为 安全约束。在关系代数中，基本操作是投影、选择、并、差、笛卡尔积，没有集合的“补”操作，因此关系代数运算总是安全的。但关系演算则不然，可能会出现无限关系和无穷验证的问题，关系演算中必须有安全约束的措施，关系演算才算是安全的。

 

关系代数表达式的优化

       如何安排关系运算中的选择、投影和连接的顺序，才能做到既省时间又省空间，执行效率高，这就是关系代数表达式的优化需要解决的问题。

       设关系 R（A，B） 和 S（C，D）都是二元关系，若有一个查询可用关系代数表达式表示：E1 = πA（σB=C ∧ D = ‘99‘（R x S））；这就不是一个好的查询，若先对 S 进行选择再相乘，性能就会提高：E1 = πA（σB=C （R x σD = ‘99‘（S）））；再仔细分析可看出，笛卡尔积和其后的选择条件 B = C 可以合并成等值连接形式，更能进一步优化：E1 = πA（R ?? B=C σD = ‘99‘（S）））。注：此处红色的 B=C 应书写在 ?? 符号下面。

 

       许多系统采用启发式优化方法对关系表达式进行优化，这种优化策略与关系的存储技术无关，主要是讨论如何合理安排操作的顺序，花费较少的时间和空间，其基本思想可表现为三条启发式规则：

1. 尽可能早的执行选择操作。
2. 尽可能早的执行投影操作。
3. 避免直接做笛卡尔积，把笛卡尔积操作之前和之后的一连串选择和投影合起来一起做。