数据库的索引原理

Posted 2020-06-17

说白了，索引问题就是一个查找问题。

　　数据库索引，是数据库管理系统中一个排序的数据结构，以协助快速查询、更新数据库表中数据。索引的实现通常使用B树及其变种B+树。
在数据之外，数据库系统还维护着满足特定查找算法的数据结构，这些数据结构以某种方式引用（指向）数据，这样就可以在这些数据结构上实现高级查找算法。这种数据结构，就是索引。

　　为表设置索引要付出代价的：一是增加了数据库的存储空间，二是在插入和修改数据时要花费较多的时间(因为索引也要随之变动)。

                            

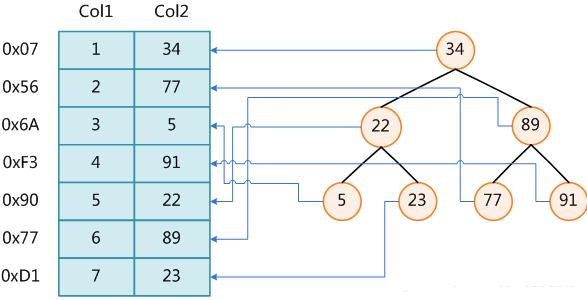
　　上图展示了一种可能的索引方式。左边是数据表，一共有两列七条记录，最左边的是数据记录的物理地址（注意逻辑上相邻的记录在磁盘上也并不是一定物理相邻的）。为了加快Col2的查找，可以维护一个右边所示的二叉查找树，每个节点分别包含索引键值和一个指向对应数据记录物理地址的指针，这样就可以运用二叉查找在O(log2n)的复杂度内获取到相应数据。

为什么需要索引

     数据在磁盘上是以块的形式存储的。为确保对磁盘操作的原子性，访问数据的时候会一并访问所有数据块。磁盘上的这些数据块与链表类似，即它们都包含一个数据段和一个指针，指针指向下一个节点（数据块）的内存地址，而且它们都不需要连续存储（即逻辑上相邻的数据块在物理上可以相隔很远）。
    鉴于很多记录只能做到按一个字段排序，所以要查询某个未经排序的字段，就需要使用线性查找，即要访问N/2个数据块，其中N指的是一个表所涵盖的所有数据块。如果该字段是非键字段（也就是说，不包含唯一值），那么就要搜索整个表空间，即要访问全部N个数据块。
    然而，对于经过排序的字段，可以使用二分查找，因此只要访问log2 N个数据块。同样，对于已经排过序的非键字段，只要找到更大的值，也就不用再搜索表中的其他数据块了。这样一来，性能就会有实质性的提升。

　

什么是索引

　　索引是对记录按照多个字段进行排序的一种方式。对表中的某个字段建立索引会创建另一种数据结构，其中保存着字段的值，每个值又指向与它相关的记录。这种索引的数据结构是经过排序的，因而可以对其执行二分查找。

　　索引的缺点是占用额外的磁盘空间。因为索引保存在MyISAM数据库中，所以如果为同一个表中的很多字段都建立索引，那这个文件可能会很快膨胀到文件系统规定的上限。

索引的原理

　　首先，来看一个示例数据库表的模式：

                       

　　注意：这里用char而不用varchar是为了精确地描述数据占用磁盘的大小。这个示例数据库中包含500万行记录，而且没有建立索引。接下来我们就分析针对这个表的两个查询：一个查询使用id（经过排序的键字段），另一个查询使用firstName（未经排序的非键字段）。

示例分析一

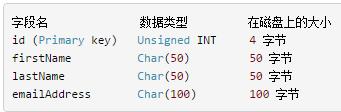
　　对于这个拥有r = 5 000 000条记录的示例数据库，在磁盘上要为每条记录分配 R = 204字节的固定存储空间。这个表保存在MyISAM数据库中，而这个数据库默认的数据库块大小为 B = 1024字节。于是，我们可计算出这个表的分块因数为 bfr = (B/R) = 1024/204 = 5，即磁盘上每个数据块保存5条记录。那么，保存整个表所需的数据块数就是 N = (r/bfr) = 5000000/5 = 1 000 000。

　　使用线性查找搜索id字段——这个字段是键字段（每个字段的值唯一），需要访问 N/2 ＝ 500 000个数据块才能找到目标值。不过，因为这个字段是经过排序的，所以可以使用二分查找法，而这样平均只需要访问log2 1000000 = 19.93 = 20 个块。显然，这会给性能带来极大的提升。

　　再来看看firstName字段，这个字段是未经排序的，因此不可能使用二分查找，况且这个字段的值也不是唯一的，所以要从表的开头查找末尾，即要访问 N = 1 000 000个数据块。这种情况通过建立索引就能得到改善。

　　如果一条索引记录只包含索引字段和一个指向原始记录的指针，那么这条记录肯定要比它所指向的包含更多字段的记录更小。也就是说，索引本身占用的磁盘空间比原来的表更少，因此需要遍历的数据块数也比搜索原来的表更少。以下是firstName字段索引的模式：

                        

　　注意：在mysql中，根据表的大小，指针的大小可能是2、3、4或5字节。

示例分析二

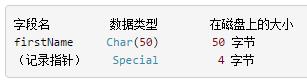
　　对于这个拥有r = 5 000 000条记录的示例数据库，每条索引记录要占用 R = 54字节磁盘空间，而且同样使用默认的数据块大小 B = 1024字节。那么索引的分块因数就是 bfr = (B/R) = 1024/54 = 18。最终这个表的索引需要占用 N = (r/bfr) = 5000000/18 = 277 778个数据块。

　　现在，再搜索firstName字段就可以使用索引来提高性能了。对索引使用二分查找，需要访问 log2 277778 = 18.09 = 19个数据块。再加上为找到实际记录的地址还要访问一个数据块，总共要访问 19 + 1 = 20个数据块，这与搜索未索引的表需要访问277 778个数据块相比，不亚于天壤之别。

什么时候用索引

　　创建索引要额外占用磁盘空间（比如，上面例子中要额外占用277 778个数据块），建立的索引太多可能导致磁盘空间不足。因此，在建立索引时，一定要慎重选择正确的字段。

　　由于索引只能提高搜索记录中某个匹配字段的速度，因此在执行插入和删除操作的情况下，仅为输出结果而为字段建立索引，就纯粹是浪费磁盘空间和处理时间了；这种情况下不用建立索引。另外，由于二分查找的原因，数据的基数性（cardinality）或唯一性也非常重要。对基数性为2的字段建立索引，会将数据一分为二，而对基数性为1000的字段，则同样会返回大约1000条记录。在这么低的基数性下，索引的效率将减低至线性查找的水平，而查询优化器会在基数性小于记录数的30%时放弃索引，实际上等于索引纯粹只会浪费空间。

查询优化器的原理

　　查询优化中最核心的问题就是精确估算不同查询计划的成本。优化器在估算查询计划的成本时，会使用一个数学模型，该模型又依赖于对每个查询计划中涉及的最大数据量的基数性（或者叫重数）的估算。而对基数性的估算又依赖于对查询中谓词选择因数（selection factor of predicates）的估算。过去，数据库系统在估算选择性时，要使用每个字段中值的分布情况的详尽统计信息，比如直方图。这种技术对于估算孤立谓词的选择符效果很好。然而，很多查询的谓词是相互关联的，例如 select count(*) from R where R.make=‘Honda‘ and R.model=‘Accord‘。查询谓词经常会高度关联（比如，model=‘Accord‘的前提条件是make=‘Honda‘），而估计这种关联的选择性非常困难。查询优化器之所以会选择低劣的查询计划，一方面是因为对基数性估算不准，另一方面就是因为遗漏了很多关联性。而这也是为什么数据库管理员应该经常更新数据库统计信息（特别是在重要的数据加载和卸载之后）的原因。（译自维基百科：http://en.wikipedia.org/wiki/Query_optimizer。）

资料出处：http://www.ituring.com.cn/article/986

   　　　　http://blog.csdn.net/kennyrose/article/details/7532032