欧拉角与四元数（计算，编程）

Posted 2020-08-25

欧拉角

 

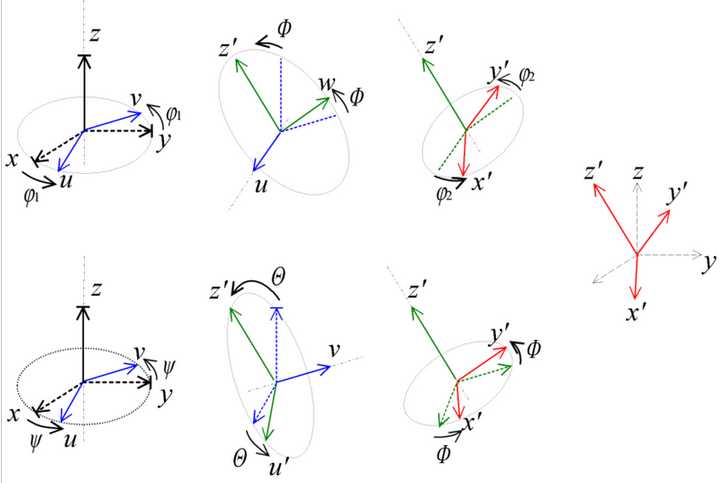
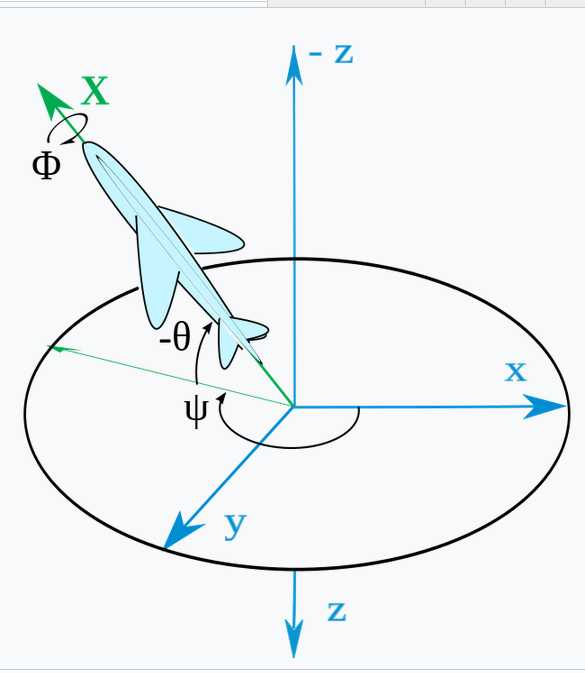
四元数计算公式

四元数的基本数学方程为 : q = cos (a/2) + i(x * sin(a/2)) + j(y * sin(a/2)) + k(z * sin(a/2)) 其中a表示旋转角度，(x,y,z)表示旋转轴

 

下面是如何把具体的四元数与旋转轴和旋转角度对应起来。

    1.指出旋转轴和旋转角度，如何转化为四元素。

    假定旋转轴是：RAxis = Z轴，换算成三维空间单位向量就是RAxis = [0 0 1],旋转60度

    那么转化成四元数就是

    q.w=cos(60°/2) = 0.866

    q.x=RAix.x*sin(60°/2) = 0*0.5=0

    q.y=RAix.y*sin(60°/2) = 0*0.5=0

    q.z=RAix.z*sin(60°/2) = 1*0.5=0.5

    例子验证：从三维空间中看，假定物体点A=[0 1 0],绕 RAxis = Z轴，旋转30度(假定顺时针为正，因为matlab就是顺时针为正，而下面的quat2dcm函数是matlab自带的)

那么物体点A旋转后在世界坐标系下的坐标将是B=[0.866 0.5 0],

如何用四元数计算出呢？思路是这样的：任何一个四元数对应着一个旋转3*3矩阵。

M=quat2dcm(q)*A‘=[0.866;0.5;0],关于quat2dcm在软件matlab里面有。

 

四元数编程

四元数的一种表示方式是： Q = xi + yj + zk + w

这儿i,  j,  k就可以看成3D 空间的3个坐标柱向量。  基于四元数的这种表示方式所以很直接他就可以被表示成一个标量w
再加上一个3维向量了。

Q = [w, v]

这里 v = xi + yj + zk

自然有一定编程经验的人会立即把这个小家伙用结构体来表示了如下：
struct quaternion
{
       double x, y, z, w;
}
这里我们没必要知道四元数的加减运算法则了，现在为了解决我们的目标（创建基于四元数的摄像机）我们第一步需要知道怎样把他标准化
。四元数的标准化和向量的标准化是一样的。目的都是将模变成1. |Q| = sqrt(w^2 + x^2 +y^2 + z^2)
下面是代码
double getLength(quaternion quat)
{
       return sqrt(quat.x * quat.x + quat.y * quat.y + quat.z * quat.z + quat.w * quat.w);
}
）
标准化的四元数 Q* = Q/|Q| = [w/|Q|, v/|Q|];
这儿是代码：
quaternion normalize(quaternion quat)
{
       double Length = length(quat);
       quat.x /= Length;
       quat.y /= Length;
       quat.z /= Lenght;
       quat.w /= Length;
       return quat;
}
下来我们需要知道怎样计算一个四元数的共轭四元数， 共轭四元数暂且用Q‘ 来代替吧。
Q‘ = [w, -v]
这儿是计算共轭四元数的代码：
quaternion conjugate(quaternion quat)
{
       quat.x = -quat.x;
       quat.y = -quat.y;
       quat.z = -quat.z;
       quat.w = -quat.w;
       return quat;
}
下面的事情就是看看怎样计算四元数的成绩了，这个貌似有点小小的复杂。
假设有四元数C , A , B 现在我们要计算 C= A* B；
具体的运算规则如下：
C.x = |A.w * B.x + A.x * B.w + A.y * B.z - A.z * B.y|
C.y = |A.w * B.y - A.x * B.z + A.y * B.w + A.z * B.x|
C.z = |A.w * B.z + A.x * B.y - A.y * B.x + A.z * B.w|
C.w = |A.w * B.w - A.x * B.x - A.y * B.y - A.z * B.z|
这儿是代码：
quaternion mult(quaternion quat)
{
      quaternion C;
      C.x = A.w*B.x + A.x*B.w + A.y*B.z - A.z*B.y;
      C.y = A.w*B.y - A.x*B.z + A.y*B.w + A.z*B.x;
      C.z = A.w*B.z + A.x*B.y - A.y*B.x + A.z*B.w;
      C.w = A.w*B.w - A.x*B.x - A.y*B.y - A.z*B.z;
      return C;
}
主要的运算讲完了，下面就要进入正题了。 现在我们是要创建摄像机了请注意。很明显在3D空间里面代表一个摄像机
就需要对这个摄像机进行定位，定向了。所以为了精确的创建摄像机，我们使用3个3维向量来代表摄像机的位置Position，观察方向View，
和摄像机的UP（这个没必要介绍吧）。对于一个第一人称的摄像机来说，我们现在就只需要考虑摄像机的旋转问题了，
使用四元数我们就可以把一个向量绕任意的柱旋转, 为了达到这个目的我们就需要首先将View向量转化成四元数，然后定义一个旋转四元数，最后应用这个旋转四元数到View四元数上就行了。下面请看具体的步骤。
为了获得View四元数，我们就要使用[w, v]来代表了。当然标量w 就设成0了。v 很显然就是View向量了。
因此四元数V（我们转化的View四元数） V = [0, View]
然后正如上面所说我们下面就要创建那个旋转四元数了，为了创建这个四元数，你就得明确你要绕哪个向量旋转了，还有旋转的角度。我们把这个柱向量（就是绕哪个向量旋转）叫做A，把旋转的角度用theta表示，那么任务即将完成了，我们创建的旋转四元数R就可以表示成：
3DVector A = [x, y , z];
R.x = A.x * sin(theta/2);
R.y = A.y * sin(theta/2);
R.z = A.z * sin(theta/2);
R.w = cos(theta/2);
下来就要进行旋转计算了：
先看看我们现在知道的量：
1. 我们有3维的View向量， 我们有View四元数 V = [0, View]
2. 假设我们要绕A向量来旋转theta度，我们有旋转四元数R来定义这次旋转。
3. 记住旋转完后我们得到的东西仍然是一个View四元数，这个自然是个新的View四元数了。我们假设他是W
所以旋转操作就是：
W = R * V * R‘
这里R是旋转四元数， V是View四元数， R‘ 是旋转四元数R的共轭四元数（其运算前面以讲了）
现在我们仅仅提取新的View四元数W的向量部分。 NewView = [W.x, W.y, W.z]
所以综上所述我们就可以创建函数来进行旋转变换：
void RotateCamera(float angle, float x, float y, float z)
{
       quaternion temp, quat_view, result;// quat_view是View四元数， temp是旋转四元数
     //  下面的三行使用旋转柱和角度计算旋转四元数
       temp.x = x * sin(angle/2);
       temp.y = y * sin(angle/2);
       temp.z = z * sin(angle/2);
       temp.w = cos(angle/2);
       // 计算View四元数
       quat_view.x = View.x; // View 是View向量
       quat_view.y = View.y;
       quat_view.z = View.z;
       quat_view.w = 0;
       //  进行旋转变换
       result = mult(mult(temp, qaut_view), conjugate(temp));
       // 得到新的View向量
       View.x = result.x;
       View.y = result.y;
       View.z = result.z;
}
至此完成。相信有一定OpenGL或D3D基础的人，很容易就把这个翻译成代码了。