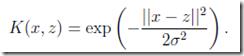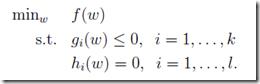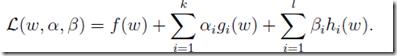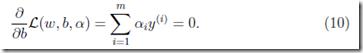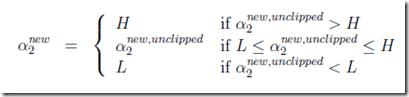支持向量机(SVM)复习总结
Posted 混沌战神阿瑞斯
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了支持向量机(SVM)复习总结相关的知识,希望对你有一定的参考价值。
摘要:
1.算法概述
2.算法推导
3.算法特性及优缺点
4.注意事项
5.实现和具体例子
6.适用场合
7.svm和感知机的异同
8.svm和LR的异同
内容:
1.算法概述
其基本模型定义为特征空间上的间隔最大的线性分类器,即支持向量机的学习策略便是间隔最大化,最终可转化为一个凸二次优化问题的求解。
或者简单的可以理解为就是在高维空间中寻找一个合理的超平面将数据点分隔开来,其中涉及到非线性数据到高维的映射以达到数据线性可分的目的。
这个最优超平面是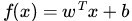 ,则对应的模型函数是
,则对应的模型函数是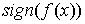 ,其中w(n维),b待定;若f(x)>0,sign(f(x))=1,否则为-1。
,其中w(n维),b待定;若f(x)>0,sign(f(x))=1,否则为-1。
2.算法推导
2.1几个基本概念:
2.1.1 函数间隔(function margin):
单个样本i的函数间隔: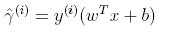 ,y取值{-1,1} ,W是参数向量,b是截距(这个margin越大,表示分类越confident )
,y取值{-1,1} ,W是参数向量,b是截距(这个margin越大,表示分类越confident )
整个样本的函数间隔: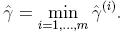 ,即最小的样本函数间隔(整体的margin由最近的那个决定的 )
,即最小的样本函数间隔(整体的margin由最近的那个决定的 )
2.1.2 几何间隔(geometric margins):
单个样本i的几何间隔: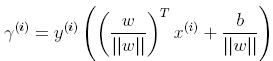 (对functional margin做了norm L1归一化)
(对functional margin做了norm L1归一化)
整个样本的几何间隔: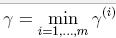
2.1.3 凸二次优化(convex optimization)问题(目标函数是结构风险最小化的):
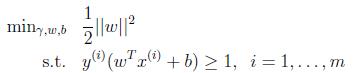 (最小化几何间隔r,并约束函数间隔rhat为1转化而来)
(最小化几何间隔r,并约束函数间隔rhat为1转化而来)
深入:凸函数与凸集杂记;andrew ng如何推导转化成的凸优化问题;
2.1.4 svm的损失函数(hinge 损失)
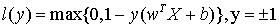
简单拆解下hinge损失的设计:上文说几何距离越远,分类越confident,而几何距离是做了归一化的,所以介于0,1之间;所以最终的损失就行就是1-y(w)
写代码(github地址)输出下hinge损失:
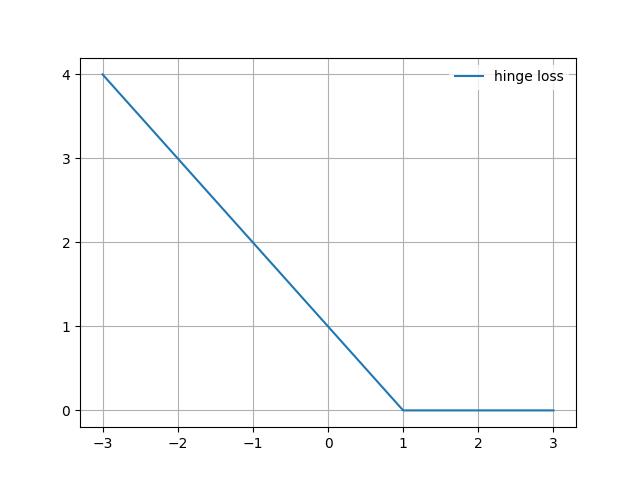
扩展:维基百科
2.1.5 核函数(Kernels function):
引入核函数的目的:
将非线性数据映射到高维的线性数据,以达到数据线性可分(<x,z> => k<x,z>)
下面推导W时我们知道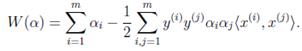 ,从而在求解W时,只要计算出x的内积即可,而这个内积可以用核函数表示
,从而在求解W时,只要计算出x的内积即可,而这个内积可以用核函数表示
几种常见的核函数:
sigmoid核: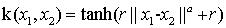
深入:证明核函数是valid ; 通过多项式核解决异或问题/代码
2.2 带约束条件的最优化解法:
2.2.1 拉格朗日乘数法(Lagrange Multiplier)
应用问题:拉格朗日乘数法是用来解决极值问题的,其将一个有n个变量与m个约束条件的最优化问题转换为一个有n + m个变量的方程组的极值问题
既有等式,也有不等式的约束,称为generalized Lagrangian
令偏导=0,
解出w和拉格朗日算子a,β,求出f(w)的极值
深入:维基百科介绍;
2.2.2 KKT(Karush-Kuhn-Tucker)约束条件
在满足KKT条件下,可以将原始问题等价于对偶问题,即d* = p*。
当原问题是凸优化问题时,KKT是原始问题能有最优化解的一个必要和充分条件
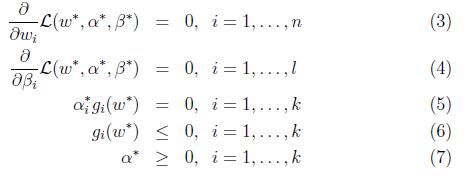
注意其中的(5), 称为KKT dual complementarity condition
要满足这个条件,α和g至少有一个为0,当α>0时,g=0,这时称“gi(w) ≤ 0” constraint is active,因为此时g约束由不等式变为等式
a>0时,对于svm就是那些support vector
2.3问题求解:
2.3.1 原始问题定义:
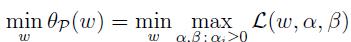 (基于上面拉格朗日乘数法的符号说明),设定对应的解为p*
(基于上面拉格朗日乘数法的符号说明),设定对应的解为p*
2.3.2 对偶问题定义:
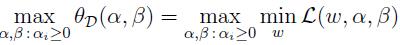 (就是交换了原始问题的min,max;并且令w为常量,a,b为变量),设定对应的解为d*
(就是交换了原始问题的min,max;并且令w为常量,a,b为变量),设定对应的解为d*
在满足KKT条件下,可以将原始问题转化为对偶问题,即d* = p*。
2.3.3 简述推导过程:
由2.1.3 凸二次优化(convex optimization)问题得到不等式约束:![]() ,凸优化函数为f(w) =
,凸优化函数为f(w) =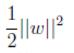 (原始凸优化问题定义)
(原始凸优化问题定义)
下面就来求解dual问题: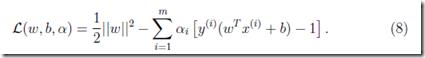 (不等式约束是仿射的,原函数是凸函数,故满足KKT条件,是强对偶解)
(不等式约束是仿射的,原函数是凸函数,故满足KKT条件,是强对偶解)
和上面讨论的广义拉格朗日 相比,注意符号上的两个变化, w变量 =>w,b两个变量 ;只有α,而没有β,因为只有不等式约束而没有等式约束
运用拉格朗日乘数法分别对w,b求导:
对w求导得 
现在把9,10,代入8,得到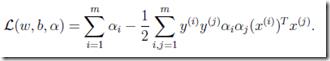 (具体推导参见)
(具体推导参见)
于是有(第一个约束本来就有,第二个约束是对b求偏导得到的结果):
最终得到如下的解:

具体的ai求解释通过SMO算法求得的
2.2.5 SMO(序列最小优化算法)
对偶优化问题:
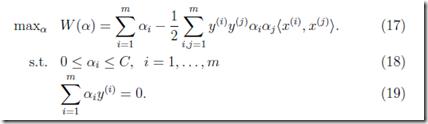 ,其中C是正则化系数(先上链接,有时间再补软间隔这部分)
,其中C是正则化系数(先上链接,有时间再补软间隔这部分)
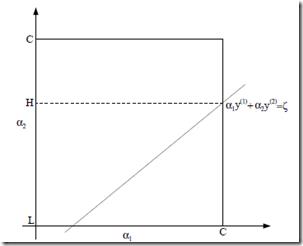
现在把α1和α2的约束用图表示出来,要保持约束就只能在这条线上移动,并且要满足a1<C
所以a2的取值在[L,H]
代入目标函数:
问题是这样求出的极值点不一定在[L,H]的范围内
所以有,在范围内最好,不在范围内的话,也需要clip到范围内
最终得a1,a2的解:
3.算法特性及优缺点
特性:支持向量是SVM的训练结果,在SVM分类决策中起决定作用的是支持向量。SVM学习问题可以表示为凸优化问题,因此可以利用已知的有效算法发现目标函数的全局最小值。而其他分类方法(如基于规则的分类器和人工神经网络)都采用一种基于贪心学习的策略来搜索假设空间,这种方法一般只能获得局部最优解。(参考自);基于结构风险最小化
优点:泛化错误率低,计算开销不大(基于结构风险最小化,使用了||w||正则项)。
高维空间下或特征维数大于样本数时仍有效(不能大得太多),小样本训练集上能够得到比其它算法好很多的结果。(在SVM分类决策中起决定作用的是支持向量)
可以灵活的指定不同的核函数(scikit官网),可以解决异或问题
缺点:大规模训练样本难以实施(存储训练样本和核矩阵(m阶)空间消耗大,时间复杂度高O(m2) )
对参数调节和核函数的选择敏感,对缺失数据敏感
原始分类器不加修改仅适用于处理二分类问题(改进:通过多个二类支持向量机的组合来解决等等);
不支持概率估计(sklearn是通过5-折交叉实现的)
高斯核容易过拟合
适用数据类型:数值型和标称型数据。
4.注意事项
标准化:基于距离的算法都要进行标准化
核函数:SVM是通过寻找超平面将数据进行分类的,但是当数据不是线性可分的时候就需要利用核函数将数据从低维映射到高维使其线性可分后,
再应用SVM理论。这时的决策函数是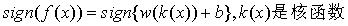
软间隔:若数据线性不可分,增加松弛变量,容忍部分样本点的函数间隔加上松弛变量大于1,这时的优化目标是: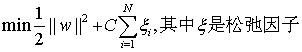
正则化:软间隔中的系数C,对应scikit-learn中svm的参数C
如何多分类:one-vs-one或者one-vs-rest,层次分类
SVM用于回归问题:SVR
SVMC常用参数(以下摘自scikit-learn):
(1)The kernel function can be any of the following:
- linear:
.
- polynomial:
.
is specified by keyword
degree,by
coef0.- rbf:
.
is specified by keyword
gamma, must be greater than 0.- sigmoid (
), where
is specified by
coef0.
(2)shrinking:whether to use the shrinking heuristics
(3)probability: whether to traina SVC or SVR model for probability estimates
(4)class_weight: set the parameter C of class ito weight*C, for C-SVC
(5)decision_function_shape : 多分类情况使用可以选择“ovo”(one vs one 的缩写),“ovr”(one vs rest的缩写),否则默认是None
(6)C:软间隔中的系数C,对应scikit-learn中svm的参数C
5.实现和具体例子(没有找到经典的应用,就直接套各种官网的例子吧)
使用one-class SVM做异常检测(附知乎介绍什么是一类支持向量)
目前支持向量机主要应用在模式识别领域中的文本识别,中文分类,人脸识别等;同时也应用到许多的工程技术和信息过滤等方面.
6.适用场合
是否支持大规模数据:线性支持;非线性不适合,暂时没找到分布式实现
特征维度:可以很高
是否有 Online 算法:线性有,非线性没有(参考自)
特征处理:支持数值型数据,类别型类型需要进行0-1编码
7.svm和感知机的异同
8.svm和LR的异同
相同点:
第一,LR和SVM都是分类算法/LR和SVM都是监督学习算法。
第二,如果不考虑核函数,LR和SVM都是线性分类算法,也就是说他们的分类决策面都是线性的。
第三,LR和SVM都是判别模型。
不同点:
第一,本质上是其loss function不同。
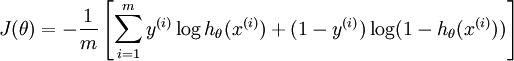
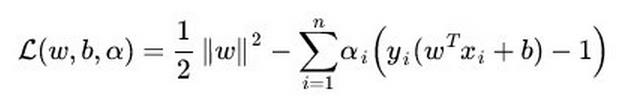
支持向量机基于几何间隔最大化原理,认为存在最大几何间隔的分类面为最优分类面 --待续
以上是关于支持向量机(SVM)复习总结的主要内容,如果未能解决你的问题,请参考以下文章
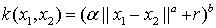 ,ng是
,ng是