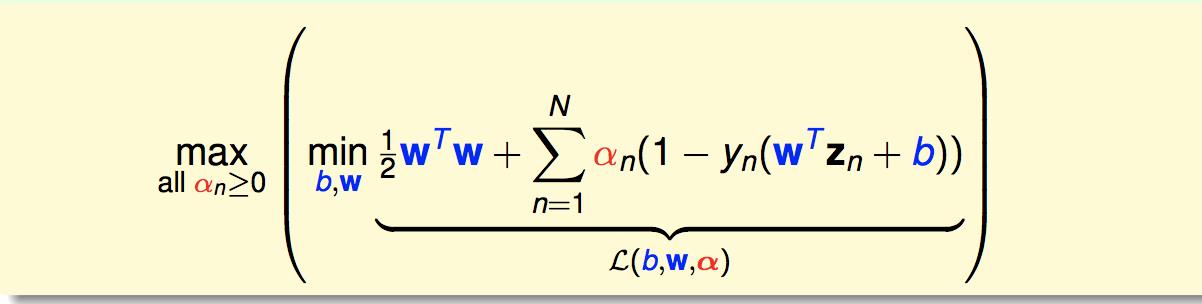对偶SVM
Posted coldyan
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了对偶SVM相关的知识,希望对你有一定的参考价值。
1.对偶问题的推导
为什么要求解对偶问题?一是对偶问题往往更容易求解,二是可以自然的引入核函数。
1.1 用拉格朗日函数将原问题转化为“无约束”等价问题
原问题是:

写出它的拉格朗日函数:

然后我们的原问题就等价为:
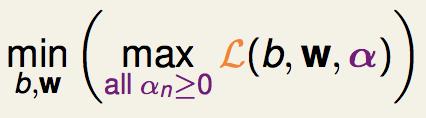
为什么可以这样等价:

即:对于不满足约束条件的(b,w),min里面趋于无穷大,因此min就把这些b,w舍去了;对于满足约束条件的解,min里面就刚好是原来的目标函数,刚好与原问题等价。
1.2 导出拉格朗日对偶问题
首先我们有如下成立:

然后我们取右边式子中的“best”阿尔法,仍然会有大于等于号成立,因为best is one of any:

这时右边的式子就是对偶问题。这里直接给出一个定理,当满足下面条件时(对于SVM来说刚好满足),原始问题和对偶问题的解是相同的:

并且它们的最优解满足KKT条件:偏导为0,对偶互补,拉格朗日乘子大于0.
1.3 用KKT条件来简化对偶问题
我们的对偶问题现在是:
根据KKT条件,我们有:
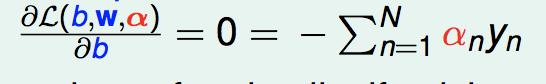
![]()
把第一个代进来:
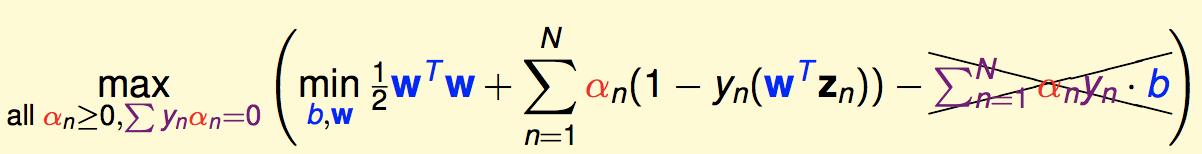
再把第二个代进来:
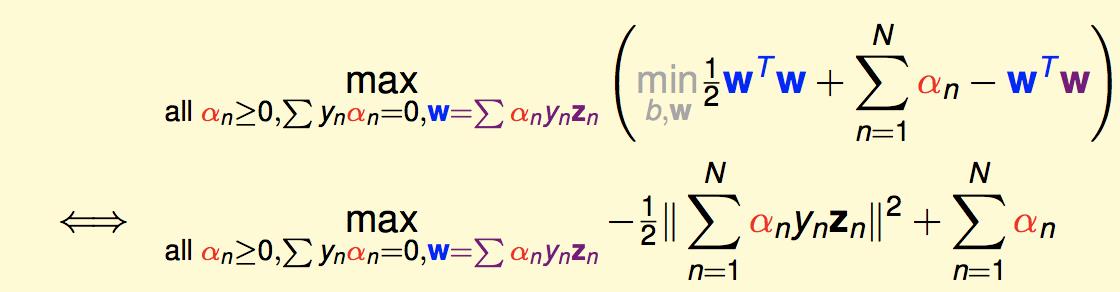
这时候,我们的问题里面就只剩一个参数阿尔法了。再把平方项展开,写的好看一点,就得到了标准的硬间隔SVM对偶问题:

2. 解对偶问题
还是解QP那一套:

之后再求W和b:
![]() (所有支持向量的加权和)
(所有支持向量的加权和)
![]() (任取一个支持向量算出)
(任取一个支持向量算出)
3. 支持向量
引出对偶问题后,我们重现定义支持向量为阿尔法大于0的向量。他们一定是在边界上的(统计学习方法p107),但是在边界上的不一定阿尔法大于0:

前面我们也提到过,w和b的计算只需要支持向量,其他向量都是无用的:
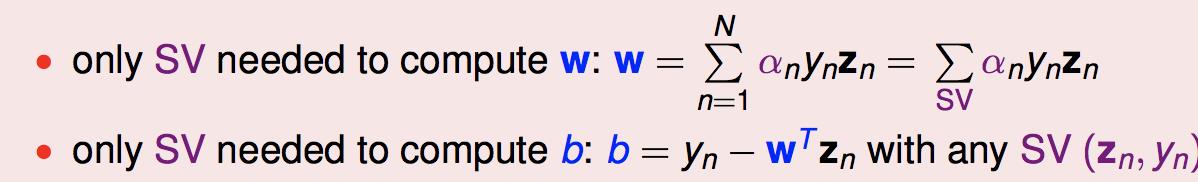
以上是关于对偶SVM的主要内容,如果未能解决你的问题,请参考以下文章