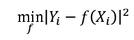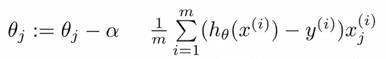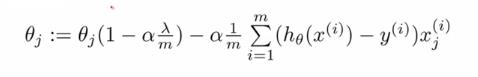过度拟合

Posted 2023-03-23

参考技术A 有些人做过大量功课，掌握了丰富数据和资料，为什么他们的决策水平，反而不如大佬短短时间内的快速判断？难道说，对一个问题思考得多，反而可能没好处吗？

如果你的模型涉及到决策判断和预测未来，那么精确写实往往不如粗略写意。事实上，你的模型越写实，你的最终效果反而可能越差！数学家，管这个叫做“过度拟合”。

结婚以后，生活满意度随着时间的变化。曲线上有10个点，对应结婚第1年到第10年的数据。

据这10个点来预测人们结婚15年甚至20年之后的幸福度，应该怎么办呢？你就需要根据现有的10个点画出一条曲线，然后再把这条曲线按照原来的趋势延伸出去。画曲线发现趋势的这个动作，就叫“拟合”。

如果曲线只是时间的函数，那么一阶多项式，f(t)=a+bt，就是假设生活满意度只和时间的一次方有关。你也可以进行二阶多项式拟合，f(t)=a+bt+ct^2，也就是生活满意度不仅和时间有关，还和时间的平方有关。以此类推，你还可以考虑更高阶的多项式拟合。

九阶多项式拟合的结果是错的离谱。

过度拟合。你的模型想要一丝不苟地反映已知的所有数据，它对未知数据的预测能力就会非常差。这是因为所谓的“已知”数据，都是有误差的！精准的拟合会把数据的误差给放大 ——拟合得越精确，并不代表预测结果就越准确，拟合得过度精确后反而结果更加糟糕。

解决：

不要想忒多。

wwg

这篇学习了之后，感觉醍醐灌顶。

做投资市场这么多年，我经常犯这样的错误

具备发掘大牛公司的能力，也发掘了一大堆牛的公司。但是总体收益虽然也是在那5%的人，但是只有长期持有这些牛股的1/10。

最大的问题就是过度拟合。

信息爆炸的年代，总是跳出来各种各样的信息。

其实每日盯盘，也是造成信息过载的重要原因。

真正的一波长逻辑，自然会有过程中的回调等，只要不是核心因素，都是噪声。

很多时候说耐心不够，其实耐心是建立在一定的基础上，那就是对信息的去繁存简。对很多噪音的屏蔽能力。

很多年前看过这样一文，共勉。

《种树郭橐驼传》，唐代文学家柳宗元的传记作品

郭橐驼，不知道他起初叫什么名字。他患了脊背弯曲的病，脊背突起而弯腰行走，就像骆驼一样，所以乡里人称呼他叫“橐驼”。橐驼听说后，说：“这个名字很好啊，这样称呼我确实恰当。”于是他舍弃了他原来的名字，也自称起“橐驼”来。

他的家乡叫丰乐乡，在长安城西边。郭橐驼以种树为职业，凡是长安城里经营园林游览和做水果买卖的豪富人，都争着把他接到家里奉养。观察橐驼种的树，有的是移植来的，也没有不成活的；而且长得高大茂盛，结果实早而且多。其他种树的人即使暗中观察、羡慕效仿，也没有谁能比得上。

有人问他种树种得好的原因，他回答说：“我郭橐驼不是能够使树木活得长久而且长得很快，只不过能够顺应树木的天性，来实现其自身的习性罢了。但凡种树的方法，它的树根要舒展，它的培土要平均，它根下的土要用原来培育树苗的土，它捣土要结实。已经这样做了，就不要再动，不要再忧虑它，离开它不再回顾。栽种时要像对待子女一样细心，栽好后要像丢弃它一样放在一边，那么树木的天性就得以保全，它的习性就得以实现。所以我只不过不妨碍它的生长罢了，并不是有能使它长得高大茂盛的办法；只不过不抑制、减少它的结果罢了，也并不是有能使它果实结得早又多的办法。别的种树人却不是这样，树根拳曲又换了生土；他培土的时候，不是过多就是过少。如果有能够和这种做法相反的人，就又太过于吝惜它们了，担心它太过分了，在早晨去看了，在晚上又去摸摸，已经离开了，又回头去看看。更严重的，甚至用指甲划破树皮来观察它是活着还是枯死了，摇晃树根来看它是否栽结实了，这样树木的天性就一天天远去了。虽然说是喜爱它，这实际上是害了它，虽说是担心它，这实际上是仇视它。所以他们都不如我。我又能做什么呢？”

问的人说：“把你种树的方法，转用到做官治民上，可行吗？”橐驼说：“我只知道种树罢了，做官治民,不是我的职业。但是我住在乡里，看见那些官吏喜欢不断地发号施令，好像是很怜爱(百姓)啊，但百姓最终反因此受到祸害。在早上在晚上那些小吏跑来大喊：‘长官命令：催促你们耕地，勉励你们种植，督促你们收获，早些煮茧抽丝，早些织你们的布，养育你们的小孩，喂大你们的鸡和猪。’一会儿打鼓招聚大家，一会儿鼓梆召集大家，我们这些小百姓停止吃早、晚饭去慰劳那些小吏尚且不得空暇，又怎能使我们繁衍生息，使我们民心安定呢？所以我们既困苦又疲乏,像这样（治民反而扰民），它与我种树的行当大概也有相似的地方吧？”

避免过度拟合之正则化（转）

避免过度拟合之正则化

“越少的假设，越好的结果”

商业情景：

当我们选择一种模式去拟合数据时，过度拟合是常见问题。一般化的模型往往能够避免过度拟合，但在有些情况下需要手动降低模型的复杂度，缩减模型相关属性。

让我们来考虑这样一个模型。在课堂中有10个学生。我们试图通过他们过去的成绩预测他们未来的成绩。共有5个男生和5个女生。女生的平均成绩为60而男生的平均成绩为80.全部学生的平均成绩为70.

现在有如下几种预测方法：

1 用70分作为全班成绩的预测

2 预测男生的成绩为80分，而女生的成绩为60分。这是一个简单的模型，但预测效果要好于第一个模型。

3 我们可以将预测模型继续细化，例如用每个人上次考试的成绩作为下次成绩的预测值。这个分析粒度已经达到了可能导致严重错误的级别。

从统计学上讲，第一个模型叫做拟合不足，第二个模型可能达到了成绩预测的最好效果，而第三个模型就存在过度拟合了。

接下来让我们看一张曲线拟合图

上图中Y与自变量X之间呈现了二次函数的关系。采用一个阶数较高的多项式函数对训练集进行拟合时可以产生非常精确的拟合结果但是在测试集上的预测效果比较差。接下来，我们将简要的介绍一些避免过度拟合的方法，并将主要介绍正则化的方法。

避免过度拟合的方法

1 交叉验证： 交叉验证是一轮验证的最简单的形式，每次我们将样本等分为k份，留一份作为测试样本并将其他作为训练样本。通过对训练样本的学习得到模型，将模型用于预测测试样本。循环上述步骤，使每一份样本都曾作为测试集。为了保持较低的方法，k值较大的交叉验证模型比较受青睐。

2 停止法： 停止法为初学者避免过度拟合提供了循环次数的指导

3 剪枝法： 剪枝法在GART （决策树）模型中应用广泛。它用于去掉对于预测提升效果较小的节点。

4 正则化： 这是我们将详细介绍的方法。该方法对目标函数的变量个数引入损失函数的概念。也就是说，正则化方法通过使很多变量的系数为0而降低模型的维度，减少损失。

正则化基础

给定一些自变量X，建立一个简单的因变量y与X之间的回归模型。回归方程类似于：

y = a1x1 + a2x2 + a3x3 + a4x4 .......

在上述方程中a1, a2, a3 …为回归系数，而x1, x2, x3 ..为自变量。给定自变量和因变量，基于目标函数估计回归系数a1, a2 , a3 …。对于线性回归模型目标函数为：

如果存在大量的x1 , x2 , x3 因变量，则可能出现过度拟合的问题。因此我们引入新的惩罚项构成新的目标函数来估计回归系数。在这种修正下，目标函数变为：

方程中的新加项可以是回归系数的平方和乘以一个参数λ。 如果λ=0 过度拟合上限的情景。λ趋于无穷则回归问题变为求y的均值。最优化λ需要找到训练样本和测试样本的的预测准确性之间的一个平衡点。

理解正则化的数学基础

存在各种各样的方法计算回归系数。一种非常常用的方法为坐标下降法。坐标下降是一种迭代方法，在给定初始值后不断寻找使得目标函数最小的收敛的回归系数值。因此我们集中处理回归系数的偏导数。在没有给出更多的导数信息前，我直接给出最后的迭代方程：

 (1)

这里的θ是估计的回归系数，α为学习参数。现在我们引入损失函数，在对回归系数的平方求偏导数以后，将转化为线性形式。最终的迭代方程如下：

 (2)

如果仔细观察该方程你会发现，ϑ每次迭代的开始点略小于之前的迭代结果。这是（1）与（2）两个迭代方程的唯一区别。而迭代方程（2）试图寻找绝对值最小的收敛的ϑ值。

结束语

在这篇文章中我们简单的介绍了正则化的思想。当然相关的概念远比我们介绍的深入。在接下来的一些文章中我们会继续介绍一些正则化的概念。

原文作者： TAVISH SRIVASTAVA

翻译： F.xy

原文链接：http://www.analyticsvidhya.com/blog/2015/02/avoid-over-fitting-regularization/

http://www.cnblogs.com/yymn/p/4646383.html