数据结构学习系列之二叉查找树

Posted 2020-08-22 Coco_酱

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据结构学习系列之二叉查找树相关的知识，希望对你有一定的参考价值。

二叉查找树（BST）是二叉树的一个重要的应用，它在二叉树的基础上加上了这样的一个性质：对于树中的每一个节点来说，如果有左儿子的话，它的左儿子的值一定小于它本身的值，如果有右儿子的话，它的右儿子的值一定大于它本身的值。

二叉查找树的操作一般有插入、删除和查找，这几个操作的平均时间复杂度都为O(logn)，插入和查找操作很简单，删除操作会复杂一点，除此之外，因为二叉树的中序遍历是一个有序序列，我就额外加上了一个中序遍历操作。

二叉树有三种遍历方式：前序遍历（pre-order）, 中序遍历（in-order）,后序遍历（post-order）。要牢记的是所谓的“前中后”指的是：当前结点是在两个子结点之前、之间、之后进行处理。

二叉查找树缺陷

如果key插入类似于随机模型，二叉查找树简洁的实现就能够提供快速的search和insert，以及rank、select、delete和范围查找等。但现实中，worst-case不是不可能发生，例如客户端完全顺序或逆序插入key。这时算法的性能将退化为N，变成线性查找，所以这种可能性也是我们寻找更好算法和数据结构的原因。

二叉查找树的应用不是很多，因为它最坏的时候跟线性表差不多，大部分会应用到它的升级版，平衡二叉树和红黑树，这两棵树都能把时间复杂度稳定在O(logn)左右。虽然不会用到，但是二叉查找树是一定要学好的，毕竟它是平衡二叉树和红黑树的基础。

接下来一步一步写一个二叉查找树。

从树开始介绍：

树的介绍

1. 树的定义

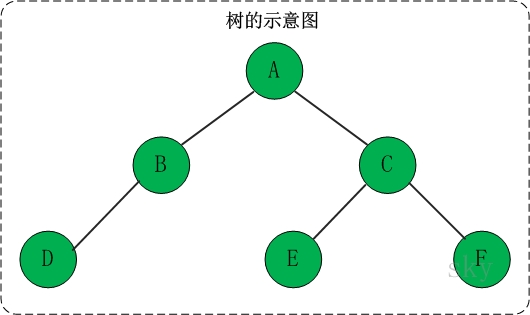
树是一种数据结构，它是由n（n>=1）个有限节点组成一个具有层次关系的集合。

把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：
(01) 每个节点有零个或多个子节点；
(02) 没有父节点的节点称为根节点；
(03) 每一个非根节点有且只有一个父节点；
(04) 除了根节点外，每个子节点可以分为多个不相交的子树。

2. 树的基本术语

若一个结点有子树，那么该结点称为子树根的"双亲"，子树的根是该结点的"孩子"。有相同双亲的结点互为"兄弟"。一个结点的所有子树上的任何结点都是该结点的后裔。从根结点到某个结点的路径上的所有结点都是该结点的祖先。

结点的度：结点拥有的子树的数目。
叶子：度为零的结点。
分支结点：度不为零的结点。
树的度：树中结点的最大的度。

层次：根结点的层次为1，其余结点的层次等于该结点的双亲结点的层次加1。
树的高度：树中结点的最大层次。
无序树：如果树中结点的各子树之间的次序是不重要的，可以交换位置。
有序树：如果树中结点的各子树之间的次序是重要的, 不可以交换位置。
森林：0个或多个不相交的树组成。对森林加上一个根，森林即成为树；删去根，树即成为森林。

二叉树的介绍

1. 二叉树的定义

二叉树是每个节点最多有两个子树的树结构。它有五种基本形态：二叉树可以是空集；根可以有空的左子树或右子树；或者左、右子树皆为空。

二叉查找树简介

二叉查找树(Binary Search Tree)，又被称为二叉搜索树。结合二分查找的高效和链表结构的灵活性。
它是特殊的二叉树：对于二叉树，假设x为二叉树中的任意一个结点，x节点包含关键字key，节点x的key值记为key[x]。如果y是x的左子树中的一个结点，则key[y] <= key[x]；如果y是x的右子树的一个结点，则key[y] >= key[x]。那么，这棵树就是二叉查找树。如下图所示：

在二叉查找树中：
(01) 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
(02) 任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
(03) 任意节点的左、右子树也分别为二叉查找树。
(04) 没有键值相等的节点（no duplicate nodes）。

插入

根据二叉查找树的性质，插入一个节点的时候，如果根节点为空，就此节点作为根节点，如果根节点不为空，就要先和根节点比较，如果比根节点的值小，就插入到根节点的左子树中，如果比根节点的值大就插入到根节点的右子树中，如此递归下去，找到插入的位置。重复节点的插入用值域中的freq标记。如图2是一个插入的过程。

插入序列：6 7 2 1 3 4

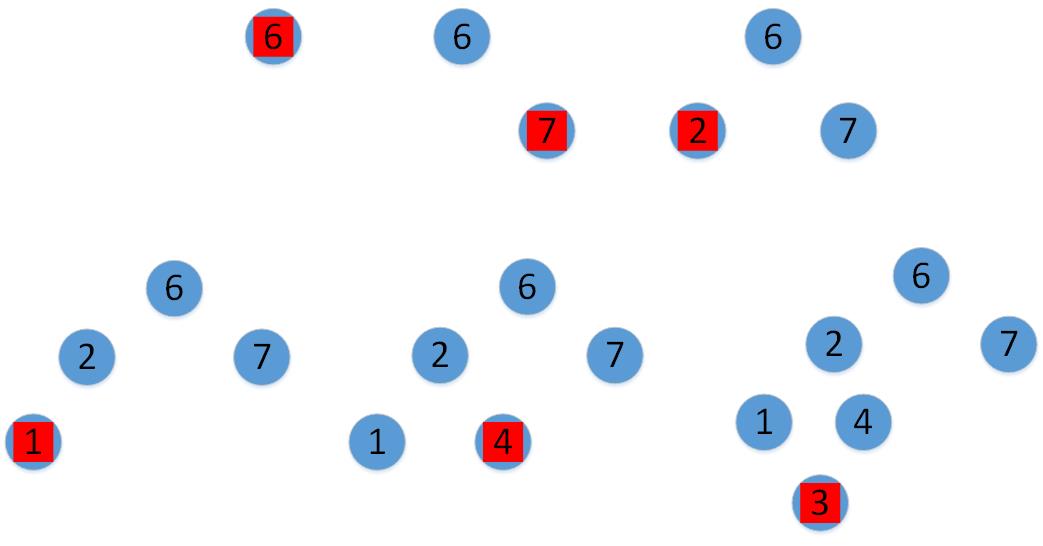
上图：一个序列的插入过程

二叉查找树的时间复杂度要看这棵树的形态，如果比较接近一一棵完全二叉树，那么时间复杂度在O(logn)左右，如果遇到如图3这样的二叉树的话，那么时间复杂度就会恢复到线性的O(n)了。

平衡二叉树会很好的解决如图3这种情况。

//插入
template<class T>
void BST<T>::insertpri(TreeNode<T>* &node,T x)
{
    if(node==NULL)//如果节点为空,就在此节点处加入x信息
    {
        node=new TreeNode<T>();
        node->data=x;
        return;
    }
    if(node->data>x)//如果x小于节点的值,就继续在节点的左子树中插入x
    {
        insertpri(node->lson,x);
    }
    else if(node->data<x)//如果x大于节点的值,就继续在节点的右子树中插入x
    {
        insertpri(node->rson,x);
    }
    else ++(node->freq);//如果相等,就把频率加1
}
//插入接口
template<class T>
void BST<T>::insert(T x)
{
    insertpri(root,x);
}

View Code

查找

查找的功能和插入差不多一样，按照插入那样的方式递归下去，如果找到了，就返回这个节点的地址，如果没有找到，就返回NULL。

二叉查找树的查找和插入过程非常相似，因为插入过程其实就是先进行查找，然后在无法找到时停止查找的那个位置执行插入。

//查找
template<class T>
TreeNode<T>* BST<T>::findpri(TreeNode<T>* node,T x)
{
    if(node==NULL)//如果节点为空说明没找到,返回NULL
    {
        return NULL;
    }
    if(node->data>x)//如果x小于节点的值,就继续在节点的左子树中查找x
    {
        return findpri(node->lson,x);
    }
    else if(node->data<x)//如果x大于节点的值,就继续在节点的左子树中查找x
    {
        return findpri(node->rson,x);
    }
    else return node;//如果相等,就找到了此节点
}
//查找接口
template<class T>
TreeNode<T>* BST<T>::find(T x)
{
    return findpri(root,x);
}

View Code

删除

对于树来说，删除是最复杂的，主要考虑两种情况。

<1>单孩子的情况

这个比较简单，如果删除的节点有左孩子那就把左孩子顶上去，如果有右孩子就把右孩子顶上去，然后打完收工。

<2>左右都有孩子的情况。

首先可以这么想象，如果我们要删除一个数组的元素，那么我们在删除后会将其后面的一个元素顶到被删除的位置，如图

那么二叉树操作同样也是一样，我们根据”中序遍历“找到要删除结点的后一个结点，然后顶上去就行了，原理跟"数组”一样一样的。

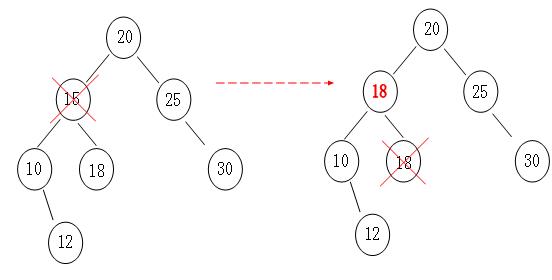
同样这里也有一个注意的地方，在Add操作时，我们将重复元素的值追加到了“附加域”，那么在删除的时候，就可以先判断是

不是要“-1”操作而不是真正的删除节点，其实这里也就是“懒删除”，很有意思。

如果删除的次数不是很多的话，有一种删除的方法会比较快一点，名字叫懒惰删除法：当一个元素要被删除时，它仍留在树中，只是多了一个删除的标记。这种方法的优点是删除那一步的时间开销就可以避免了，如果重新插入删除的节点的话，插入时也避免了分配空间的时间开销。缺点是树的深度会增加，查找的时间复杂度会增加，插入的时间可能会增加。

//删除
template<class T>
void BST<T>::Deletepri(TreeNode<T>* &node,T x)
{
    if(node==NULL) return ;//没有找到值是x的节点
    if(x < node->data)
    Deletepri(node->lson,x);//如果x小于节点的值,就继续在节点的左子树中删除x
    else if(x > node->data)
    Deletepri(node->rson,x);//如果x大于节点的值,就继续在节点的右子树中删除x
    else//如果相等,此节点就是要删除的节点
    {
        if(node->lson&&node->rson)//此节点有两个儿子
        {
            TreeNode<T>* temp=node->rson;//temp指向节点的右儿子
            while(temp->lson!=NULL) temp=temp->lson;//找到右子树中值最小的节点
            //把右子树中最小节点的值赋值给本节点
            node->data=temp->data;
            node->freq=temp->freq;
            Deletepri(node->rson,temp->data);//删除右子树中最小值的节点
        }
        else//此节点有1个或0个儿子
        {
            TreeNode<T>* temp=node;
            if(node->lson==NULL)//有右儿子或者没有儿子
            node=node->rson;
            else if(node->rson==NULL)//有左儿子
            node=node->lson;
            delete(temp);
        }
    }
    return;
}
//删除接口
template<class T>
void BST<T>::Delete(T x)
{
    Deletepri(root,x);
}

View Code

遍历

遍历即将树的所有结点访问且仅访问一次。按照根节点位置的不同分为前序遍历，中序遍历，后序遍历。

前序遍历：根节点->左子树->右子树

中序遍历：左子树->根节点->右子树

后序遍历：左子树->右子树->根节点

例如：求下面树的三种遍历

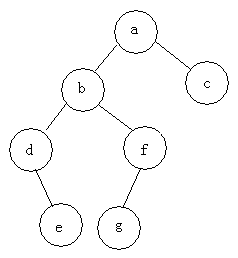
前序遍历：abdefgc

中序遍历：debgfac

后序遍历：edgfbca

/*以前序遍历为例采用递归的方法实现
 * 前序遍历"二叉树"
 */
template <class T>
void BSTree<T>::preOrder(BSTNode<T>* tree) const
{
    if(tree != NULL)
    {
        cout<< tree->key << " " ;
        preOrder(tree->left);
        preOrder(tree->right);
    }
}

template <class T>
void BSTree<T>::preOrder() 
{
    preOrder(mRoot);
}